bzoj 2152

太久没碰点分治的我看见这题已经失了智...

首先这种统计肯定要想一想点分，当然也有树形dp的做法，不过还是用点分吧...

我们每次找到一个根，然后统计以这个根为中心，模3为0，1,2的路径数量（这一点可以直接搜索），然后做个卷积统计一下即可

但是可能会出现重复的情况，重复来源于这种时候：

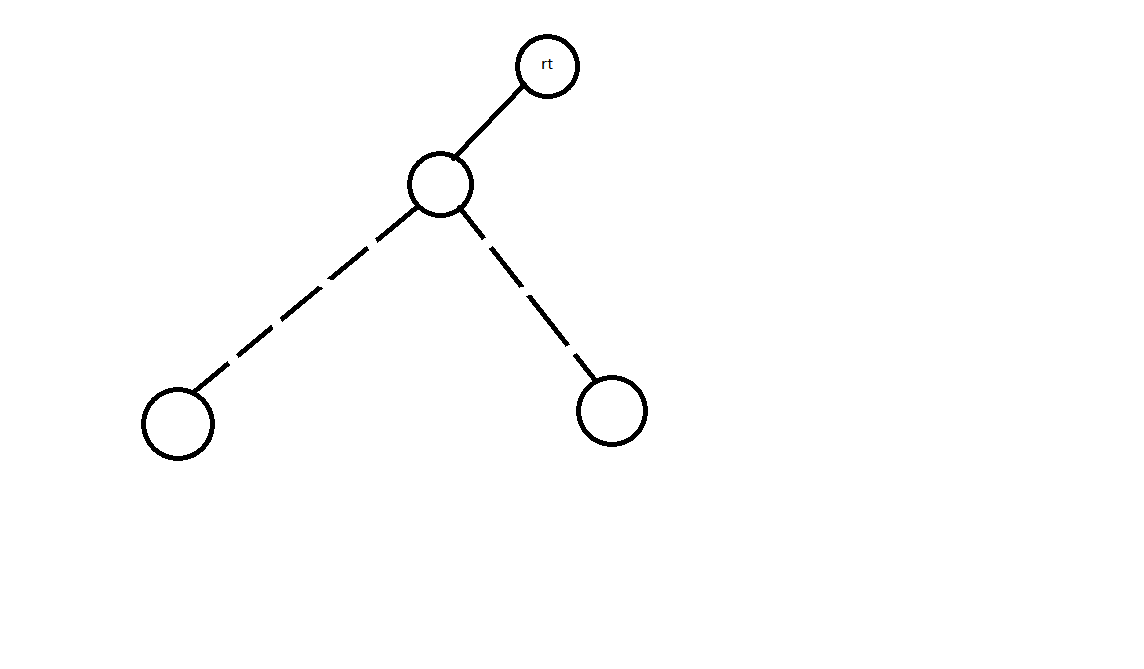
如图所示，这样的路径（也就是两条虚线构成的路径）其实不应该在统计当前的$rt$之下，但是我们这种统计方式会导致这种情况统计重复！

因此我们需要去掉这种情况

这样我们在当前根的每一个子节点下再搜一遍，去掉这一堆贡献即可

贴代码：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
struct Edge
{
    int nxt;
    int to;
    int val;
}edge[40005];
int head[20005];
int dep[20005],my_stack[2000005];
int siz[20005],maxp[20005];
bool vis[20005];
int ttop;
int f[5];
int ans=0;
int cnt=1;
int n,rt,s;
int gcd(int x,int y)
{
    return y?gcd(y,x%y):x;
}
void add(int l,int r,int w)
{
    edge[cnt].nxt=head[l];
    edge[cnt].to=r;
    edge[cnt].val=w;
    head[l]=cnt++;
}
void get_rt(int x,int fx)
{
    siz[x]=1,maxp[x]=0;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int to=edge[i].to;
        if(to==fx||vis[to])continue;
        get_rt(to,x);
        siz[x]+=siz[to];
        maxp[x]=max(maxp[x],siz[to]);
    }
    maxp[x]=max(maxp[x],s-siz[x]);
    if(maxp[x]<maxp[rt])rt=x;
}
void dfs(int x,int fx,int dep)
{
    my_stack[++ttop]=dep;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int to=edge[i].to;
        if(to==fx||vis[to])continue;
        dfs(to,x,dep+edge[i].val);
    }
}
int calc(int x,int olen)
{
    int ret=0;
    ttop=0;
    dfs(x,0,0);
    f[0]=f[1]=f[2]=0;
    for(int i=1;i<=ttop;i++)f[my_stack[i]%3]++;
    for(int i=0;i<=2;i++)ret+=f[i]*f[(6-i-olen%3)%3];
    return ret;
}
void solve(int x,int fx)
{
    ans+=calc(x,0);
    vis[x]=1;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int to=edge[i].to;
        if(to==fx||vis[to])continue;
        ans-=calc(to,2*edge[i].val);
        rt=0,s=siz[to];
        get_rt(to,x),solve(rt,x);
    }
}
int main()
{
    scanf("%d",&n);
    maxp[0]=0x3f3f3f3f;
    for(int i=1;i<n;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z),add(y,x,z);
    }
    rt=0,s=n;
    get_rt(1,1);
    solve(1,0);
    int t=gcd(ans,n*n);
    printf("%d/%d\n",ans/t,n*n/t);
    return 0;
}