后缀自动机复习笔记
首先发现原来的理解好乱啊...这次换一种理解的方式吧...
设原串为一个长度为$n$的字符串$T$
我们考虑这个字符串的每一个子串$S$,用一个集合$endpos_{S}$代表$S$在$T$中出现的所有右端点的集合
例:$T="aaabc"$,$S="aaab"$,则$endpos_{S}=${$4$}(下标从1开始是个比较好的主意qwq)
那么考虑另一个问题:这个串的所有子串的$endpos$两两不同吗?
显然不是的,因为显然$S="aab",S="ab",S="b"$时均有$endpos_{S}=${$4$}
那么我们称这些东西构成了$endpos$的一个等价类,用$len$来记录这个等价类中长度最长的字符串的长度,在这个例子中,显然最长的字符串是$"aaab"$,因此$len=4$
接下来考虑几个性质:
如果我们在一个子串之前加入一个字符$c$得到一个新的子串,那么这两个子串的$endpos$之间会有什么关系呢?
很显然,$endpos_{'c'+S}\subseteq endpos_{S}$!
这是比较显然的,因为如果$'c'+S$在位置$p$出现过,那么$S$一定在位置$p$出现过
那么基于这些包含关系,我们事实上可以把这些不同的$endpos$等价类引出父子关系!
举个例子:
$T="acbc"$
列个表格:
| a | b | c | ac | bc | acb | cbc | cb | acbc | |
| endpos | 1 | 3 | 2,4 | 2 | 4 | 3 | 4 | 3 | 4 |
那么我们把这些等价类引出这样的关系,立刻得到:
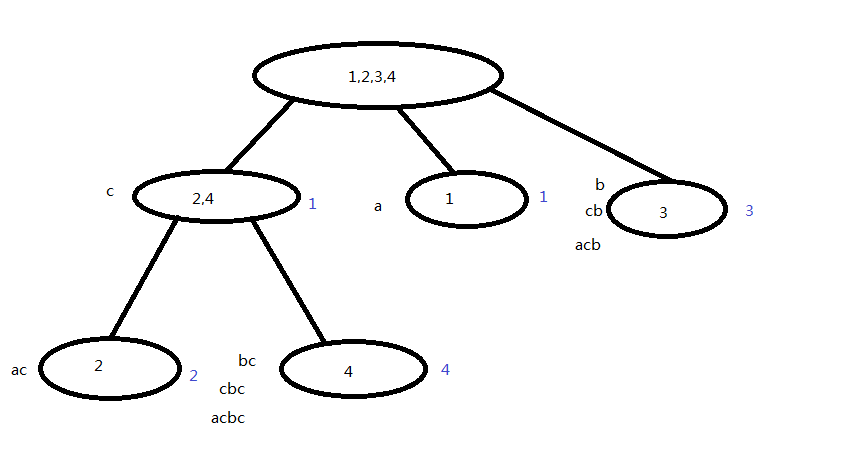
这是一个树形结构!
父节点一定是子节点的后缀!
我们已经知道后缀自动机了,因此你或许能看出这就是parent树!
当然,我们把顺序反过来了...先出了parent树
这玩意有啥用?
可能没啥用,但是...我们基于这一点能更好的理解后缀自动机!
接下来考虑后缀自动机:
在这个基础上来理解后缀自动机,就比较容易了:后缀自动机其实是一个有向无环图,他能够识别这个字符串的所有子串,而不是这个字符串字串的串则一定不能被识别!
同时,后缀自动机需要维护一些指针(注意不是有向无环图的边),使得按照这些指针能形成上面那样的树形结构,而这个树形结构从某种意义上将才是后缀自动机的核心!
这里也就是说,刚才那棵树上的节点就是后缀自动机上的所有节点!
因此我们在构建后缀自动机的时候,不妨考虑一直维护这棵树的性质,理解起来可能会容易一些:
从一个简单的例子入手:
例:$T="acc"$
首先我们插入第一个节点$a$:
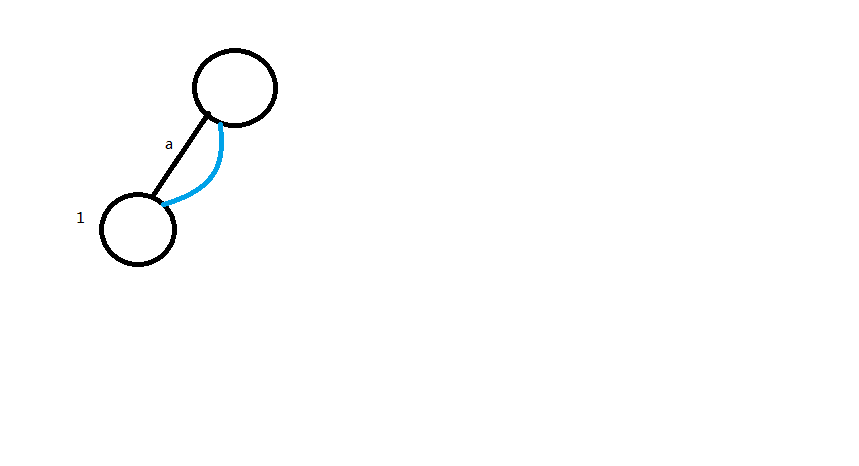
这个好理解,蓝色的是我们维护的指针,黑色的是DAG的边
再插入第二个节点$c$,得到:
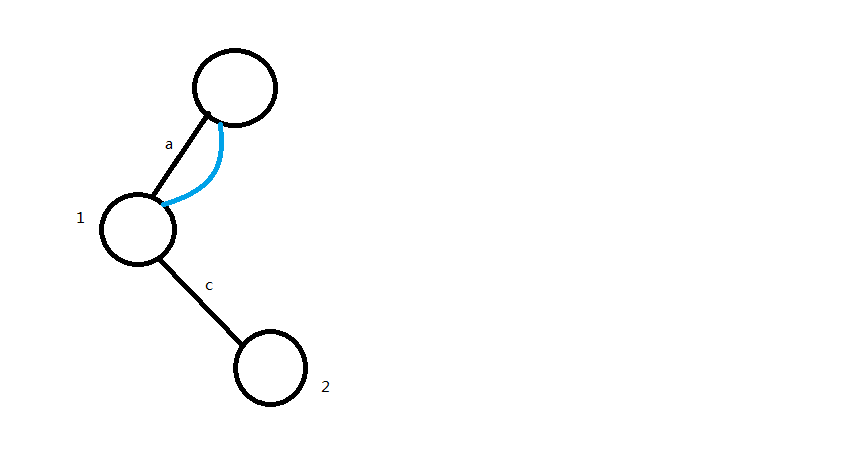
这里开始出现几个小问题:
第一个:出边怎么连?
直觉告诉我们:应该直接顺着上一个节点连出来
可是首先我们知道,后缀自动机应当能够接受这个字符串的所有子串,可这样根本没有办法接受子串$"c"$嘛!
那么这么看来,我们其实应该补上一些出边
怎么补呢?
我们知道,加入一个新的节点以后,产生的新的无法被识别的字符串一定是新串的一个后缀!
因此如果需要补充出边,我们一定要补全识别这些后缀
而新串的一个后缀去掉这个新的节点以后得到的是什么?
原串的后缀!
如何找到原串的后缀呢?
直接顺着指针往上跳嘛!
对于跳到的节点,补上新节点这个出边就好了嘛!
回到这个例子,我们补全之后的后缀自动机应该长这个样子:
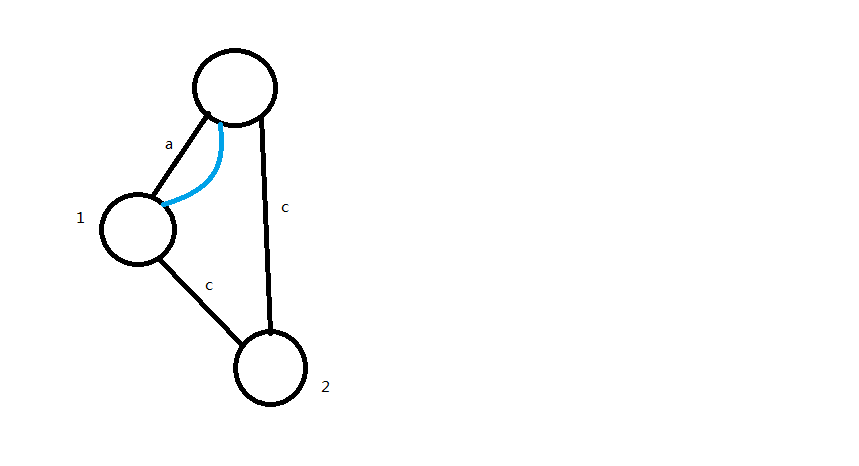
接下来,我们考虑维护新加入的节点的指针
显然没有等价类的关系,直接指回根节点即可
就是这样:
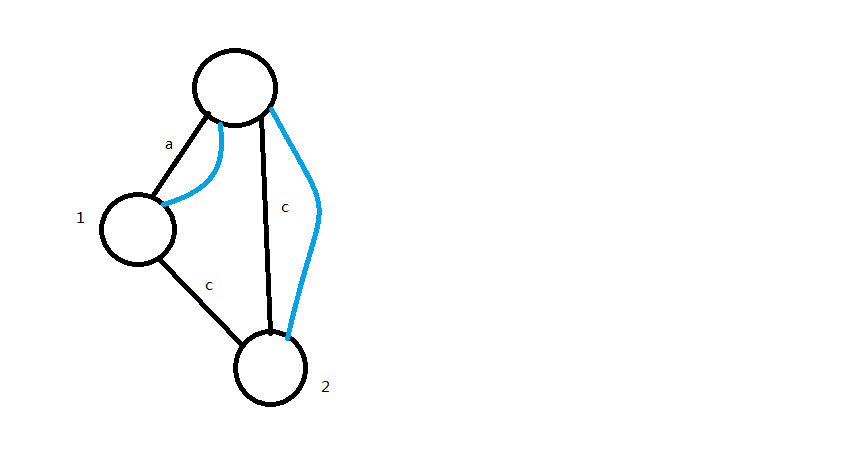
接下来,加入下一个节点:
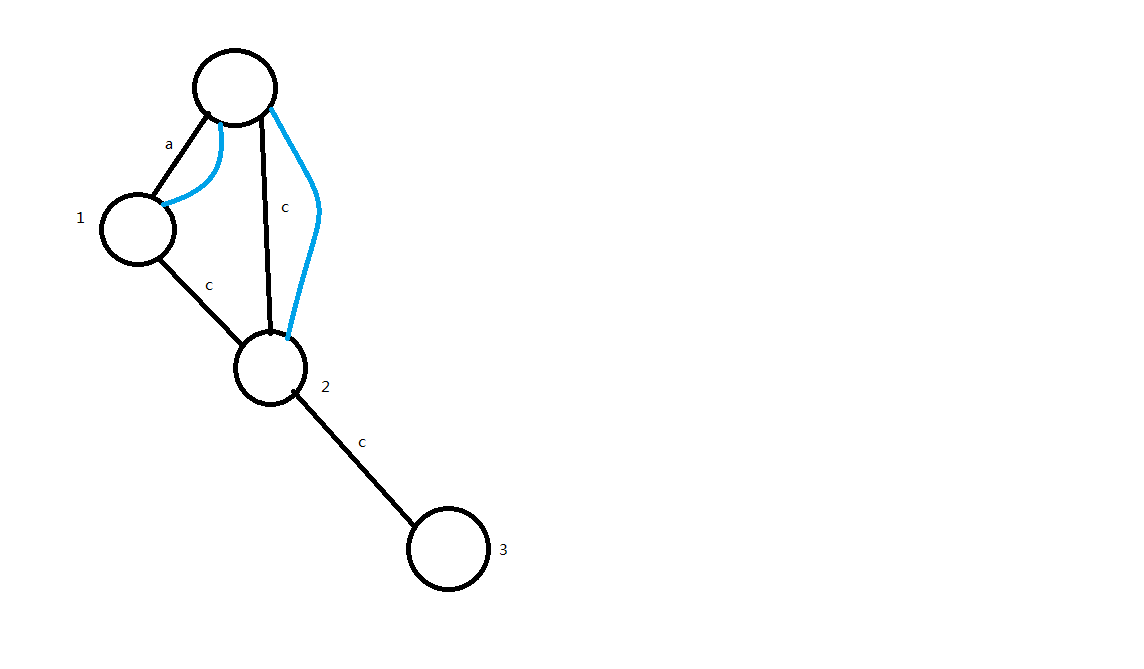
好像很友好
但还是上面两个问题:
怎么维护出边?
顺着指针往上跳?
可是...这次跳到的点已经有这个出边了!
那怎么办?
有点麻烦了...
更麻烦的还在下面!
我们标记一下这几个点:
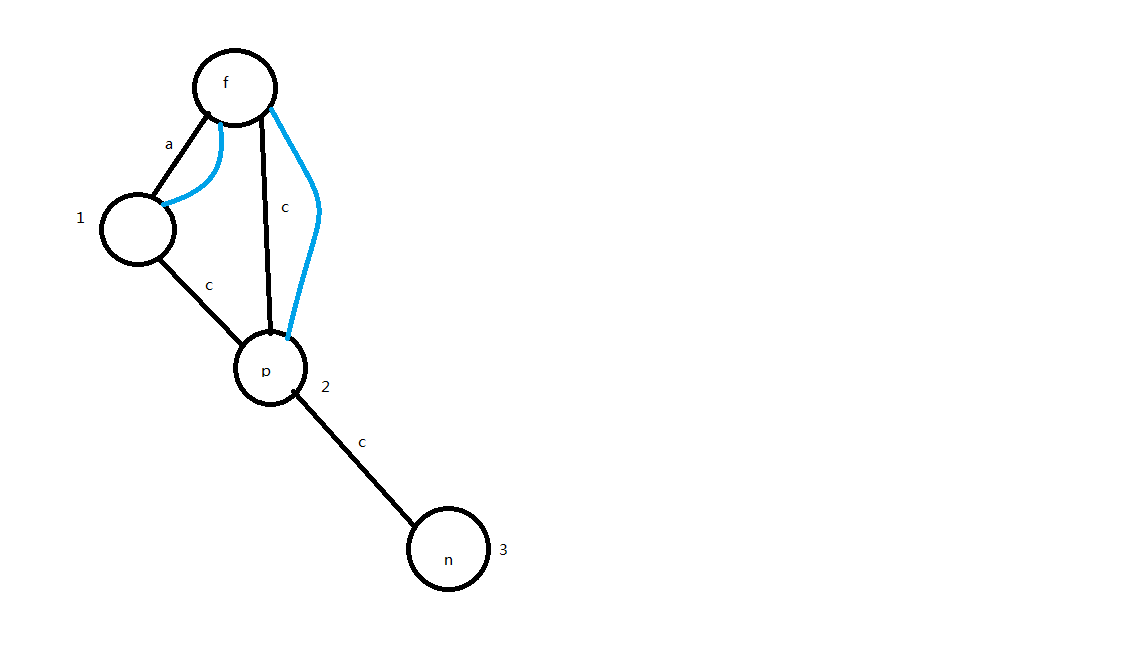
然后分析一下$len$的关系:
发现$l_{p}>l_{f}+1$!
这说明什么?
这说明$p$等价类中的一些串是不能通过单纯在$f$等价类后面添加一个字母得到的!
那么就产生了一个问题:当加入一个新节点$n$以后,节点$p$产生了信息的丢失!
为什么?
原来,$endpos_{p}=${$2$},他维护了两个子串:$"ac"$和$"c"$,而$l_{p}=2$(来源于子串$"ac"$),也就是说我们实际上藏起来了$"c"$这个串
但是,当我们再次引入$"c"$这个节点时,子串$"ac"$的$endpos$没有变,然而子串$"c"$的$endpos$却发生了改变,这样的话把$"ac"$和$"c"$放在一起是不合法的!
因此我们需要重新构造了
我们把这个压缩节点展开,新建一个节点,就是:
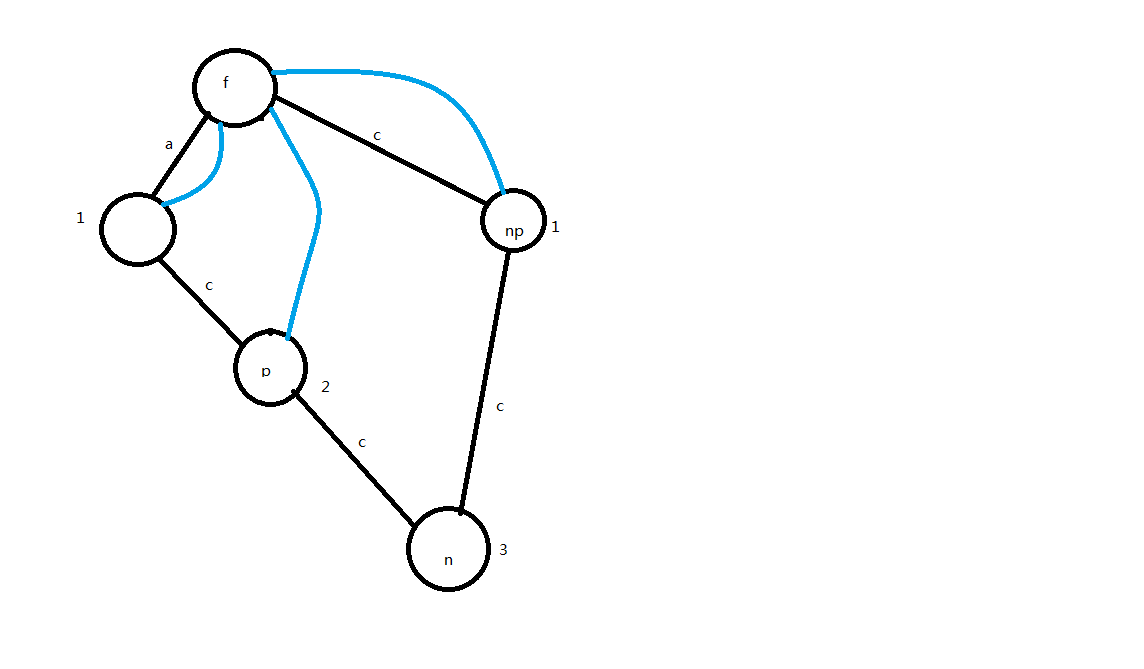
(由于分裂了这个节点,我们应该把$p$的所有信息继承给$np$,只修改$len$即可)
同时发现$p$的指针需要修改了,因为他的$endpos$是$np$的$endpos$的一个子集,因此改一下指针,就得到:

好像还差个新节点的指针没处理啊...
直接指向新建的节点就可以了,因为此时满足$len_{np}=len_{f}+1$
等等,为什么这样就可以直接建立呢?
考虑$len_{np}-len_{f}=1$,也就是说明$np$这个节点上只维护了一个字符串,这个字符串没有压缩信息,而且加入了新的第$i$个字符以后这个节点的$endpos$集合同时增加了一个$i$,那么仍然保证$endpos$集合的正确性
所以在一开始处理的时候,如果本来就能满足这个条件,也就不需要分裂节点了
所以完整的后缀自动机就长成了这个样子:

如果我们把蓝色的线拎出来,就能看到一棵树形结构了
同时我们发现,父子节点之间的$len$的差值就是子节点自己这个$endpos$等价类中串的个数(很显然,一个等价类中的串长连续)
这样后缀自动机和parent树就都搞出来了



 浙公网安备 33010602011771号
浙公网安备 33010602011771号