决策树算法(一）

 一、概述

        决策树（Decision Tree）是一种基本的分类与回归方法，其主要优点是模型具有可读性。决策树学习算法通常是一个递归地选择最优的特征，并根据该特征对训练数据进行分割，使得对各个数据集有一个最好的分类的过程。学习的过程一般为如下几个步骤：

• 特征选择：从训练数据的特征中选择最优特征作为当前节点的分裂标准（特征选择的标准不同产生了不同的特征决策树算法）。
• 决策树生成：根据所选特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树。
• 剪枝：决策树容易过拟合，需要剪枝来缩小树的结构和规模（包括预剪枝和后剪枝）

        决策树的生成对应着模型的局部选择（局部最优），决策树的剪枝对应着全局选择（全局最优）。常有的算法有ID3、C4.5、CART。对于不同的算法，特征选择与数据处理的方式不同，如下

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益比（信息增益高于平均水平）	支持	支持	支持
CART	分裂回归	二叉树	分类：基尼系数 回归：均方差	支持	支持	支持

二、特征选择

2.1 熵和条件熵

在信息论和概率统计中，熵（entropy）是表示随机变量不确定性的度量。熵越大，随机变量的不确定性就越大。求得H(Y)

 

 

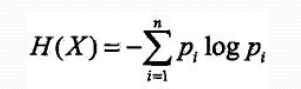
条件熵H(Y|X)：表示在己知随机变量X的条件下随机变量Y的不确定性，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：

 

 

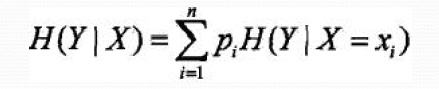
 2.2.信息增益

信息增益(Information gain)表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。—般地，熵H(Y)与条件熵H(Y|X)之差称为互信息（mutual information).决策树学习中的信息增益等价于训练数据集中类与特征的互信息。找到使信息增益大的特征。

信息增益的算法步骤：

1. 输入：训练数据集D和特征A；

2. 输出：特征A对训练数据集D的信息增益g(D,A)

3. 1、计算数据集D的经验熵H(D) 

                

             2、计算特征A对数据集D的经验条件熵H(D|A)

               

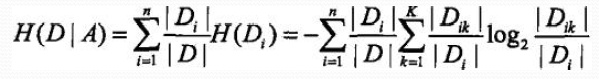
             3、计算信息增益: g(D,A)=H(D)-H(D|A).

通俗的说：熵可以理解为数据的混乱程度，对于尚未进行分类的数据肯定是比较乱的，如果通过分类对其进行整理，那么数据就不乱了，这和我们收拾房间的道理是一样的。那么怎么样分类能够让屋子看着更干净整洁呢？通过颜色，把白色的裤子和衣服放一起，其他颜色衣服裤子的放在一起，还是通过衣服的属性分类，衣服放在一起，裤子放在一起，哪个看着最整洁呢？可以用一个值衡量这个特征的贡献（最初始的屋子状态（打分为5），现在的状态（最干净为1，一般为2，还是乱为3），注：熵越大，屋子越乱）。差值越大，越整洁，此时的特征就是最优的特征。

 2.3.信息增益比

特征A对训练数据集D档信息增益比定义为:

 2.4基尼系数

分类问题中，假设有 K 个类，样本点属于第k 类的概率为  ，则概率分布的基尼系数定义为

对于二分类问题，若样本点属于第一个分类的概率是 p ，则概率分布的基尼系数为

对于给定的样本集合D ，其基尼系数为

其中，  是  中属于第  类的样本子集，  是类的个数。

如果样本集合 D 根据特征 A 是否取某一可能值 a 被分割成  和  两部分，即

则在特征 A 的条件下，集合 D 的基尼系数定义为

基尼系数Gini(D) 表示集合 D 的不确定性，基尼系数Gini(D,A)  表示经A=a 分割后集合 D 的不确定性。基尼系数值越大，样本集合的不确定性也就越大。

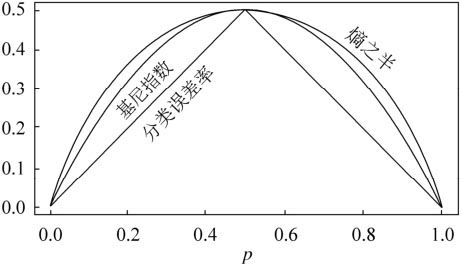
对于二类分类，基尼系数和熵之半的曲线如下：

　从图可以看出，基尼系数和熵之半的曲线非常接近，仅仅在45度角附近误差稍大。因此，基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时，为了进一步简化，CART分类树算法每次仅仅对某个特征的值进行二分，而不是多分，这样CART分类树算法建立起来的是二叉树，而不是多叉树。这样一可以进一步简化基尼系数的计算，二可以建立一个更加优雅的二叉树模型。