字符串奇怪题

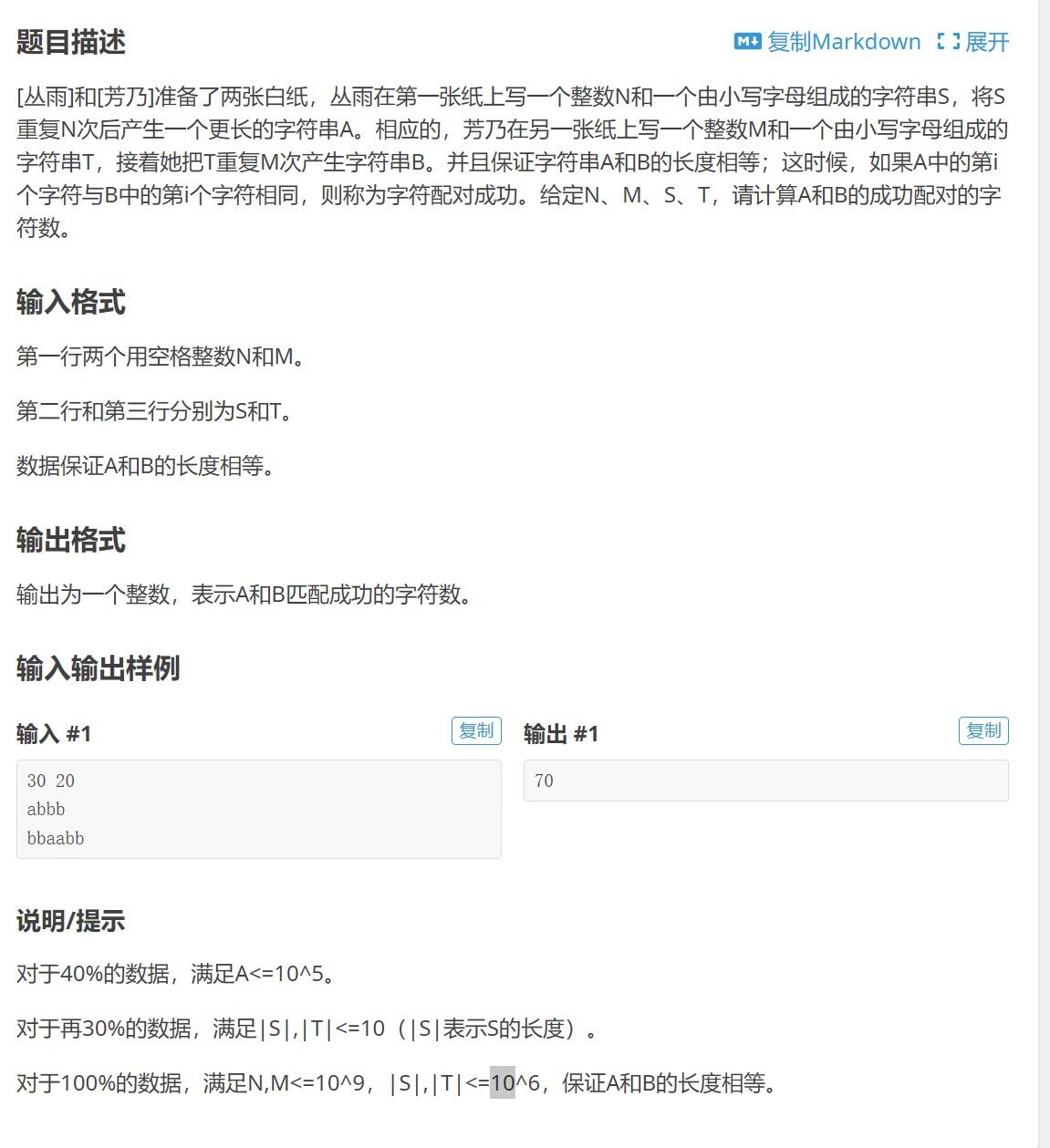
考虑S第一个字符，会和T中哪些位置上的数配对。

其实就是 \(k|S|\mod |T|\)。

然后可以打表找规律：

int main() {
    int a, b;
    cin >> a >> b;
    int x = 0;
    vector<int> all;
    while (x < a * b) {
        all.push_back(x % b);
        x += a;
    }
    sort(all.begin(), all.end());
    for (int i : all) cout << i << ' ';
    return 0;
}

发现序列和\(gcd(|S|,|T|)\)有关，具体来说是\(d = gcd(|S|,|T|)\)，那么先有 \(d\) 个0，\(d\) 个 \(d\)，\(d\) 个 \(2d\) ，……，一直到\(d\)个\(kd,(k+1)d\ge|T|\)。

那么对于这个位置的贡献，只需要枚举\(T\)中\(kd\)位置的值，判断是否相等，如果是就加上\(d\)的贡献。

比如长度分别是12和20。

x=0：0 0 0 0 4 4 4 4 8 8 8 8 12 12 12 12 16 16 16 16 。
x=1：1 1 1 1 5 5 5 5 9 9 9 9 13 13 13 13 17 17 17 17 。
x=2：2 2 2 2 6 6 6 6 10 10 10 10 14 14 14 14 18 18 18 18 。
x=3：3 3 3 3 7 7 7 7 11 11 11 11 15 15 15 15 19 19 19 19 。
x=4：0 0 0 0 4 4 4 4 8 8 8 8 12 12 12 12 16 16 16 16 。
……

不难发现，从x=k的地方出发，相当于以\(d\)为循环节，首项是\(k\mod d\)，公差是\(d\)的数列。

写出如下无关\(n, m\)的代码：

int main() {
	cin >> a >> b >> s >> t;
	int d = gcd(s.size(), t.size());
	int res = 0;
	for (int x = 0; x < s.size(); x ++ ) {
		int cnt = 0;
		for (int y = x % d; y < t.size(); y += d)
			if (s[x] == t[y]) cnt ++ ;
		res = res + cnt * d;
	}
	cout << res << endl;
	return 0;
}

复杂度\(O(\frac{|S||T|}{d})\)。

由于\(0,4,8,...\),\(1,5,9,...\),\(2,6,10,...\)在\(T\)中对应的字符是一样的，产生了冗余计算，我们考虑将它们放在一起算。

我们关心的只是某个字母的出现次数，统计即可。

int main() {
	cin >> a >> b >> s >> t;
	int d = gcd(s.size(), t.size());
	int res = 0;
	for (int x = 0; x < d; x ++ ) {
		memset(cnt, 0, sizeof cnt);
		for (int i = x; i < t.size(); i += d)
			cnt[t[i] - 'a'] ++ ;
		for (int i = x; i < s.size(); i += d)
			res = res + cnt[s[i] - 'a'] * d;
	}
	cout << res << endl;
	return 0;
}

对于\(T_i\)，只会在\(x = i \mod d\)的时候被枚举到一次，\(S_i\)同理。

复杂度 \(O(|S|+|T|)\)。

---

对拍证明，上述算法是正确的。

数据生成器：

int main() {
	srand(time(0));
	int n, m;
	n=rand()%1000000+1,m=rand()%1000000+1;
	long long t=n*m/gcd(n,m);
	if (t/n>1e9||t/m>1e9) printf("%d %d\n", n, m);
	else printf("%lld %lld\n", t/n, t/m);
	while (n--) putchar(rand()%26+'a');
	putchar('\n');
	while (m--) putchar(rand()%26+'a');
	return 0;
}

PS：那个打表的证明：0.7节