【算法进阶课】图论笔记

网络流的基本概念

• 做题方法：先将原问题转化成网络流模型，再检验图是否和原问题等价。
• 流网络：一张有向图，图中可以存在环，有一个源点和一个汇点。打个比方，源点相当于出水口，边相当于水管，汇点相当于能够容纳无穷多水的大海，边的容量 \(c(u,v)\) 就是水管每秒能够通过的最多的水量，也就是一个限制。
• 一般地，图中不存在反向边。一条边的容量 \(c=0\) 意味着没有这条边。

假如存在反向边，可以通过如下操作将图变为不存在反向边的图，从而简化问题。

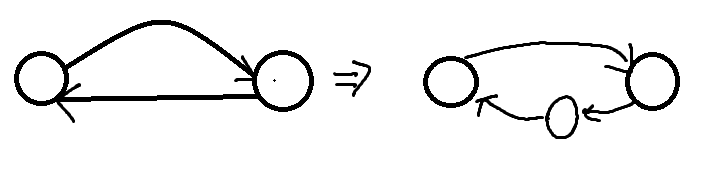
• 可行流，可以理解为水管中实际的流量，边 \((u,v)\) 上的可行流记为 \(f(u,v)\)。可行流需要满足两个条件：

1. 容量限制：\(0 \le f(u,v) \le c(u,v)\)。
2. 流量守恒：不是源点和汇点的中间节点，流入该点的可行流之和等于流出该点的可行流之和。也就是中间节点不存储流量。

• 可行流的流量 \(|f|\) ：源点流出的可行流和减去流入源点的可行流和。
• 最大流：最大可行流，即 \(|f|\) 的最大值。
• 残留网络：对于\(G\)的一个可行流\(f\)，记\(G_f\)为它的残留网络。残留网络中的点集就是原点集，边集是原边集加上反向边。对于原边集的边，\(c'(u,v)=c(u,v)-f(u,v)\)；对于反向边\(c'(u,v)=f(v,u)\)。
• 定理：\(G\)中一个可行流\(|f|\)对应的残留网络的一个可行流\(|f'|\)，\(|f|+|f'|\)也是\(G\)的一个可行流。（注意：此处相加不是简单数值相加，对于正向边是数值直接相加\(f+f'\)，而反向边是\(f-f'\)）。从容量限制和流量守恒两方面进行简单分类讨论即可证明。在数值上，\(|f+f'|=|f|+|f'|\)。（看源点来证明，因为流量的定义只与源点有关）

对于一个点，\(f\) 和 \(f'\)的流量直接相加，肯定还是守恒的。（\(a=b,c=d\rightarrow a+c=b+d\)）但这样有个问题，就是原图中没有反向边，这个方案不是一个可行流。记某一条反向边的流量为 \(x\)，把这条反向边的流量删去，假如该边在残留网络中是流入的边，那么流入量\(c \leftarrow c - x\)，它在 \(G\) 中是流出的边，那么流出量 \(b \leftarrow b - x\)，又\(a+c=b+d\rightarrow a+c-x=b-x+d\)。此时流量依然守恒，并且反向边没有流量，可以看成删去了反向边，这就是一个可行流了。这种方式就对应了上面的流的加法。

• 增广路径：残留网络中一条从源点到汇点的简单路径（无环），且路径上的容量均大于 \(0\) 的一条路径，叫做增广路径。
• 割：将点集\(V\)划分为两个子集\(S\),\(T\)，且\(S \cup T = V\)，\(S \cap T = \phi\)，\(s \in S\)，\(t \in T\)（\(s,t\)分别是源点和汇点）的过程叫做网络的一个割。
• 割的容量：\(c(S,T) = \sum{c(u,v)}(u \in S, v \in T)\)。
• 最小割：最小容量的割。（弹幕：类比水流，相当于弄一个截面来计算单向水流量）
• 共有 \(2^{n-2}\) 种割：除了源点和汇点，其它点各有两种选择。
• 割的流量：对于\(u \in S, v \in T, a \in T, b \in S\)，\(f(S,T)=\sum{(f(u,v)-f(a,b))}\)。（从S流到T减去从T流到S）。
• 对于任何一个割，任何一个可行流 \(|f|\)，都有 \(f(S,T) \le c(S,T)\)，\(f(S,T)=|f|\)。
• 定义 \(f(X,Y)\) 表示从集合 \(X\) 流向 \(Y\) 的流量（从X流到Y的减去从Y流到X的），则有如下性质：

1. \(f(X,Y)=-f(Y,X)\)。
2. \(f(X,X)=0\)。
3. \(f(Z, X \cup Y)=f(Z,X)+f(Z,Y)\)，其中 \(X \cap Y = \phi\)。
4. \(f(X \cup Y, Z)=f(X,Z)+f(Y,Z)\)，其中 \(X \cap Y = \phi\)。（相当于把\(X \cup Y\)拆成两部分看）

• 运用上述性质可以证明\(f(S,T)=|f|\)：
  \(f(S,V)=f(S,S)+f(S,T)\)，又\(f(S,S)=0\)，所以\(f(S,T)=f(S,V)=f({s},V)+f(S-{s},V)\)。后面一项相当于除了源点和汇点（本来S就没有汇点t），中间结点的流量和，由于流量守恒，所以是0。所以\(f(S,T)=f({s},V)\)，根据定义\(f(S,T)=|f|\)。

\(f(S-{s},V)\) 可以看成一堆流出的，减去一堆流入的，然后因为加法有交换律和结合律，你把从 \(u\) 流出的，和从 \(u\)流入的，结合到一起算，都是 \(0\)（\(u\)流量守恒）。

• 于是 \(\forall f, c(S,T), |f| = f(S,T) \le c(S,T)\)，最大流是\(f_m\)，最小割\(c_m(S,T)\)，因为这个式子恒成立，所以 \(|f_m| \le C_m(S,T)\)

• 最大流最小割定理（下述三个条件互为充要条件，对于一个流网络 \(G = (V,E)\)）：

1. \(|f|\) 是最大流；
2. \(|f|\) 的残留网络中不存在增广路；
3. 存在某个割 \([S,T]\)，\(|f|=c(S,T)\)。

上面的证明方式可以积累：1推2，2推3，3推1，即可证明它们互为充要条件。

• \(1 \rightarrow 2\) ：假设存在增广路，因为增广路走过的路径流量均为正，取流量的最小值就是一个可行流，并且流量为正，这是一个残留网络的可行流，\(|f| + |f'| > |f|\)，与 \(f\) 是最大流矛盾。

• \(2 \rightarrow 3\)：

1. 定义 \(S\) 为从 \(s\) 出发，在残留网络中沿着正容量的边走，能到达的所有点的集合。
2. \(T=V-S\)，则 \([S,T]\) 为原图的一个合法割。
3. 有如下性质：\(\forall u \in S, v \in T, f(u,v)=c(u,v), f(v,u)=0\)（注意此处 \((u, v), (v, u)\) 均为原图中的边，不包括残留网络中的反向边），反证法会发现，如果不满足这两个条件，\(T\)中的点就可以被\(s\)遍历到，矛盾。

借助残留网络构造原流网络的一个割，因为它们点集相同。假如不满足 \(f(u,v)=c(u,v)\)，那么在残留网络中 \(u\)就可以通过大于0的边走到\(v\)（\(c'(u, v) = c(u, v) - f(u, v) > 0\)），那么 \(v\) 就不在 \(T\) 中了；假如不满足 \(f(v,u)=0\)，同样在残留网络中 \(u\)可以走到 \(v\)（\(c'(u, v) = f(v, u) > 0\)），矛盾。

4. 所以

\[|f|=f(S,T)=\sum_{u \in S, v \in T, (u, v) \in G}{f(u, v)} - \sum_{u \in S, v \in T, (v, u) \in G}{f(v, u)} = \sum_{u \in S, v \in T, (u, v) \in G}{c(u, v)} = c(S,T) \]

• \(3 \rightarrow 1\)：假设最大流是 \(f_m\)，最小割是 \(c_m(S,T)\)，则 \(|f| \le |f_m|,c(S,T)\ge c_m(S,T)\)，又 \(|f| = c(S,T) \ge c_m(S,T) \ge |f_m|\)，也就是 \(|f| \le |f_m|, |f| \ge |f_m|\)，所以 \(|f| = |f_m|\)。

事实上，此时这个割就是最小割。\(c_m(S,T) \ge |f| = c(S,T)\)，又 \(c_m(S,T) \le c(S,T)\)，所以 \(c_m(S,T) = c(S,T)\)。由于 \(1\)和\(3\)等价，那么最大流就等于最小割。

最大流之算法模板

\(FF\)：在流网络中随便找一个可行流，然后维护残留网络，找增广路，加上增广路的贡献，直到不存在增广路。

找增广路相当于判断 \(s\) 和 \(t\) 的连通性。

更新的时候，对于每一条边更新即可。

EK复杂度 \(O(nm^2)\)

Dinic复杂度 \(O(n^2m)\)

但是网络流的复杂度上界很松。一般来说：\(O(n+m)=O(10000)\)时，用EK；\(O(n+m)=O(100000)\)时，用Dinic。

Dinic 算法的正确性证明，时间复杂度证明比较复杂度，不必纠结。

1. 用 BFS 建立分层图；
2. 用 DFS 找出所有增广路（只能在层级之间行走），并进行更新。

注意： Dinic 和 EK 都是维护残留网络

Dinic 算法有很多奇怪的优化，虽然复杂度是 \(O(n^2m)\) ，但实际运行的效率可以看成是线性的。 Dinic 算法对优化非常的敏感，如果优化加的不好，就会TLE。

当前弧优化：比如当前到了 \(u\) 这个点，要遍历它的后继的时候是按照邻接表的顺序遍历的，如果有一条边的容量已经是 \(0\) 了，那么也就没有必要再遍历它了（不是指进入遍历子图，而是说 for 循环中经过一下它），一个点貌似无关紧要，但是遍历了一半之后会有相当于总点数 \(N\) 级别的点无需遍历，这个优化对于时间复杂度的优化还是很可观的。

最初的时候每一条边都要遍历，也就是 cur[u] = h[u]。

关于为何要建立分层图， BFS 的时候仍然可以直接 return true ：能够抵达汇点 T 的点一定是在 T 前面一层，而搜到 T 了说明上一层的所有点都已经入队了，都已经分配好层数了。而层数大于等于 T 的点，也不可能会扩展到 T ，所以不用管了。

大概理解一下 DFS 中 flow 和 limit 的作用，比如你到了点 u ，有一条增广路可以到 T ，但是还有另外一条也可以到 T ， EK 算法就是先把前面这条增广了，更新残留网络，再找下一条；但是其实 S 到 u 的这些点不用重复遍历一次了， Dinic 直接在 u 的时候把另外一条就增广了（ EK 就是会把到 u 的路上的容量全部减掉某个数，再重新走一遍，到 u 之后再走另一条，这里省去这些时间）。也可以理解为找到了一个残留网络的可行流而非简单的增广路径。（不是简单的直的路径了）