P6186 [NOI Online #1 提高组] 冒泡排序
引入
随便给出一组数据:
5 3 1 2 4
初始逆序对数量: \(6\)。
冒泡排序
一轮:3 1 2 4 5 \(6-4=2\)。
两轮:1 2 3 4 5 \(2-2=0\)。
逆序对块
观察会发现,数 \(x\) 会一直后退,直到有一个大于 \(x\) 的数 \(y\),\(y\) 也会一直后退……
后退数将区间划分成了一个个逆序对块。
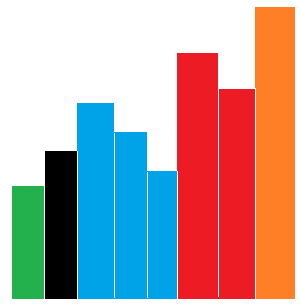
上图是序列中数的大小的柱状图,其中,不同颜色分别代表了不同逆序对块。
为什么要定义逆序对块呢?其实这是我为了分析方便自己编的一个东西()。
逆序对块的性质:
- 逆序对块第一个的数是逆序对块中数的最大值。
- 每个逆序对块的第一个数单调递增。
- 每个逆序对块的第一个数 \(a_x\) 是 \(max(a_i), 1 \le i \le x\)。
性质1是由定义导出的。
性质2:假设不成立,那么存在两个逆序对块,使得块1的第一个数 \(x\) 大于 块2的第一个数 \(y\),根据性质1,第二个块中所有数都严格小于 \(x\) ,所以块2可以接到块1后面。
性质3:由性质2,对于任何一个逆序对块的第一个数 \(a_x\),一定大于它前面任何一个逆序对块的第一个数;而根据性质1,每个逆序对块中的第一个数都是块的最大数,所以 \(a_x\) 前面的逆序对块中的所有数都小于 \(a_x\)。
分析
我们发现,逆序对 \((x,y)\) 是一个二元组,直接统计是 \(O(N^2)\) 的,考虑将其归类为一个一维的集合。
PS:其实归并排序求逆序对也是对逆序对进行了分类统计。
将逆序对 \((x, y)\) 归类到 以 \(y\) 结尾的逆序对集合。
定义数 \(f(x)\) 是以 \(x\) 结尾的逆序对集合的元素个数(方便后面分析)。
容易发现,每个逆序对块中,进行一轮冒泡排序之后,除了第一个数,后面的数的 \(f(x)\) 都会减一。
假设第一个数是 \(a_1\) ,那么它一定大于逆序对块中的其它数,所以对于其它数的 \(f(x)\) 有大小为 \(1\) 的贡献,而排序之后它会一直后退,这个大小为 \(1\) 的贡献就没了,所以要减一。
也就是下图:
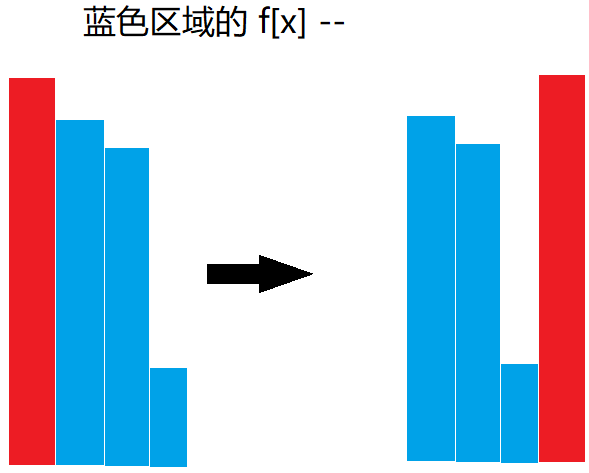
根据定义,一开始的逆序对个数就是 \(sum(f(i)), 1 \le i \le n\) 。
第一轮排序之后,逆序对个数变成了 \(f_1 + f_2 - 1 + ... + f_n\) ,由上面的分析,除了逆序对块第一个数,其 \(f(x)\) 都会减一;由性质3,\(f(x)=0\) 的数就是逆序对块的第一个数,所以答案总共减去了 \(n - cnt(f(x)==0)\)。
第二轮排序同理,就是在第一轮排序的基础上进行这个操作。
...
数学化:
设 \(s[i]\) 为 \(f[x] = i\) 的 \(x\) 个数。
第一轮排序 \(f_1 + f_2 + ... + f_n - (n - s[0]) = f_{1-n} - n + s[0]\)。
第二轮中新增的 \(f_x = 0\) 的个数就是原来 \(f_x = 1\) 的个数,因为 \(1 - 1 = 0\)。
第二轮排序 \(f_{1-n} - n + s[0] - (n - s[0] - s[1]) = f_{1-n} - 2n + (2s[0] + s[1])\)
形式化的,第 \(k\) 轮排序之后就会是 \(f_{1-n} - kn + ks[0] + (k-1)s[1] + ... + s[k - 1]\)。
这样讨论修改时就可以不去想象逆序对的变化了,只要对着式子分析即可。
记 \(ans_i\) 为第 \(i\) 轮排序后的答案。
由冒泡排序相关知识,只要记录到 \(ans_{n-1}\)即可。
容易发现,\(s[i]\) 只会对 \(ans_{j}, i+1 \le j \le n-1\) 产生影响。
交换 \(w[a]\) 和 \(w[b]\) ,一下讨论 \(w[a] > w[b]\) 的情况,另一种情况类似。
注意这里的变量名都是交换前的变量名。
交换之后 $f[b] -- $,导致 $f_{1-n} -- $,也就是 $ans_{0-n-1} -- $。
这样会导致 $s[f[b]] -- , s[f[b] - 1] ++ $,先看前者。
\(s[f[b]]\) 对 \(ans[f[b]+1]\)及其后面产生影响。
\(ans[f[b]+1] = ... + s[f[b]]\),\(-1\)。
\(ans[f[b]+2] = ... + 2s[f[b]] + s[f[b]+1]\),\(2(s[f[b]]-1)=2s[f[b]]-2\),整体 \(-2\)。
依此类推……
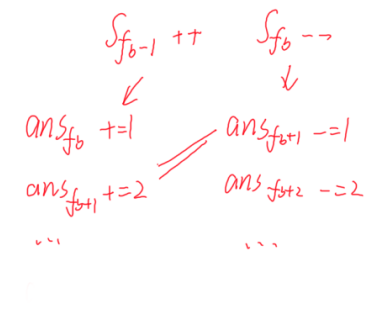
我们会发现,这两个操作合在一起,会让 \(ans_j ++ , f_b \le j \le n - 1\)
代码实现:
求 \(f(x)\) ,可以在值域上建立树状数组统计。
修改操作是区间修改,每次查询是单点查询,可以用树状数组维护一个差分数组 \(B\) ,前缀和就是变化量,加上原值就是答案。
需要注意的是,因为树状数组的下标最小是1,而\(ans\)的下标最小是0,所以要加上1个偏移量(+1)。
/*
id: luogu P6186
start: 0:01
end: 0:31
debug:
ver: II
*/
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 5e5 + 10;
struct BinTree
{
LL c[N];
int n;
BinTree(int n = 0)
{
this->n = n;
}
void add(int x, LL k)
{
while (x <= n)
{
c[x] += k;
x += x & -x;
}
}
// 返回[1,x]的和
LL ask(int x)
{
LL ans = 0;
while (x)
{
ans += c[x];
x -= x & -x;
}
return ans;
}
};
BinTree tr, B;
int w[N], n, q;
LL ans[N]; // 第k轮冒泡后的答案
int f[N]; // f[i]: w[i]前面大于w[i]的数的个数
int s[N]; // s[i] 表示f[j]=i的f[j]的个数
void inp()
{
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
}
void init()
{
tr.n = n;
for (int i = 1; i <= n; i ++ )
{
f[i] = i - 1 - tr.ask(w[i]); // [1,w[i]]
s[f[i]] ++ ;
ans[0] += f[i];
tr.add(w[i], 1);
}
// 最多进行i-1轮
LL t = s[0]; // 初始逆序对块的第一个数的个数
for (int i = 1; i < n; i ++ )
{
ans[i] = ans[i - 1] - n + t;
t += s[i];
}
}
void out()
{
B.n = n;
while (q -- )
{
int t, c;
scanf("%d%d", &t, &c);
// 别忘记这句!
c = min(c, n - 1);
if (t == 1)
{
int a = c, b = c + 1;
if (w[a] > w[b])
{
B.add(1, -1);
B.add(f[b] + 1, 1);
f[b] -- ;
swap(w[a], w[b]);
swap(f[a], f[b]);
}
else
{
B.add(1, 1);
B.add(f[a] + 2, -1);
f[a] ++ ;
swap(w[a], w[b]);
swap(f[a], f[b]);
}
}
else printf("%lld\n", ans[c] + B.ask(c + 1));
}
}
int main()
{
inp();
init();
out();
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号