2025.7.21 【B】CSP-J模拟赛8

咕了好久……

T1 无限重复

简单题，找出字符串 \(t\) 中的字母在字符串 \(s\) 中的相对顺序，对于 \(t_i\) 和 \(t_i+1\)，设其字母分别为 \(t1\) 和 \(t2\) ，若满足 \(l_{t1}>l_{t2}\) （\(l_a\) 表示字母 \(a\) 在字符串 \(s\) 中的位置），则贡献为1，反之贡献为0；

代码如下：

#include<bits/stdc++.h>
using namespace std;
string s,t;
int tn[30],lj[30][30],ans=1;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>s>>t;
	for(int i=0;i<26;i++){
		tn[s[i]-'a']=i;
	}
	for(int i=0;i<26;i++){
		for(int j=0;j<26;j++){
			if(tn[i]==tn[j]) lj[i][j]=1;
			else if(tn[i]<tn[j]) lj[i][j]=0,lj[j][i]=1;
			else lj[i][j]=1,lj[j][i]=0;
		}
	}
	for(int i=0;i<t.size()-1;i++){
		ans+=lj[t[i]-'a'][t[i+1]-'a'];
	}
	cout<<ans;
	return 0;
}

T2 两个数组

对于%42的数据，容易想到一个超级朴素 \(O(n^5)\) 暴力（虽然只能获得33分

考虑优化，赛时想到了昨天比赛中说的前缀和优化dp，那么对于这道题也可以用类似的思想

设 \(dp_{i,j,k}\) 表示当前选到第 \(i\) 位，\(a_i=j,b_i=k\) 的方案数，\(t_{j,k}\) 表示之前 \(a\) 数组选到 \(j\) ，\(b\) 数组选到 \(k\) 的方案数，那么初始化 \(dp_{0,1,n}=1,t_{1,n}=1\) ；

每次更新时，枚举 \(i,j,k\) ，\(t_{j,k}=t_{j,k}+t_{j-1,k}+t_{j,k-1}-t_{j-1,k-1}%mod\) ，\(dp_{i,j,k}=t_{j,k}\) ，\(t_{j,k}=dp_{i,j,k}\) ，应该挺好想的，每次继承当前情况的答案，下次更新时直接用就行 ；

最后枚举 \(i,j\) ，累计每一种情况的答案，\(ans=ans+dp_{m,i,j}%mod\) ；

放上代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e9+7;
ll n,m,dp[15][1005][1005],t[1005][1005],ans;
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>n>>m;
	dp[0][1][n]=1,t[1][n]=1;
	for(ll i=1;i<=m;i++){
		for(ll j=1;j<=n;j++){
			for(ll k=n;k>=j;k--){
				t[j][k]+=t[j-1][k]+t[j][k+1]-t[j-1][k+1];
				t[j][k]%=mod;
				dp[i][j][k]+=t[j][k];
				dp[i][j][k]%=mod;
				t[j][k]=dp[i][j][k];
			}
		}
	}
	for(ll i=1;i<=n;i++){
		for(ll j=n;j>=i;j--){
			ans+=dp[m][i][j];
			ans%=mod;
		}
	}
	cout<<ans;
	return 0;
}

T3 蚂蚁V2/P5835 [USACO19DEC] Meetings S

蚂蚁V8【激昂】

清晰地记得以前做过的，但是考场就是想不起来 （悲

我们发现一次相撞后两个蚂蚁原路返回，但是速度等其他信息均不变，我们可以看成两只蚂蚁相互穿过，并交换了自己的体重。在这个过程中，向左走的蚂蚁总数（设其为 \(sum1\) ）和向右走的蚂蚁总数（设其为 \(sum2\) ）是分别不变的，我们统计出每只蚂蚁按照这个思路的掉落时间，也就是其距离朝向端木棍端点的距离；

我们又发现，一只蚂蚁最终掉落在左侧，必须要求初始在他左侧的蚂蚁全部掉落，右侧同理，那么最终在左边掉落的蚂蚁一定是最左边的 \(sum1\) 只蚂蚁，在右边掉落的蚂蚁一定是最右边的 \(sum2\) 只蚂蚁，并且其掉落时间是相对应的；

如下图，这是视为穿过时每只蚂蚁凋落的时间，\(a_i,b_i\) 表示向右/左走第 \(i\) 只蚂蚁掉落时间

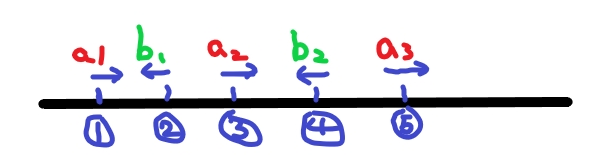
那么实际情况中每只蚂蚁的掉落时间其实是这样的：

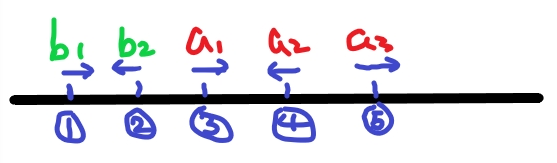
可能有点抽象，但是手%一下可以发现这个是完全正确的

我们处理出每只蚂蚁的掉落顺序然后排序，可以计算出当掉落蚂蚁的体重超过总和的一半时的时间，然后放到最开始的蚂蚁位置中使用二分（或双指针），统计与自己方向相反且距离不超过时间二倍的蚂蚁即可（但是主播在这里偷懒了，因为数据过水，所以用一个 \(1/4*n^2\) 的统计也可以水过这道题）；

#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e4+5;
int n,L,maxt,suma,sumb,cnt1,cnt2,wht,zt;
int fi_t,ans=0;
struct node{
	int w,x,d,tim;
}e[MAXN],tl[MAXN],tr[MAXN];
bool cmp(node a,node b){
	return a.x<b.x;
}
bool wht_cmp(node a,node b){
	return a.tim<b.tim;
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>n>>L;
	for(int i=1;i<=n;i++){
		cin>>e[i].w>>e[i].x>>e[i].d;
		zt+=e[i].w;
	}
	sort(e+1,e+n+1,cmp);
	for(int i=1;i<=n;i++){
		if(e[i].d>0){
			sumb++;
			tr[sumb].d=e[i].d,tr[sumb].w=e[i].w,tr[sumb].x=e[i].x;
			tr[sumb].tim=L-e[i].x-1;
		}
		if(e[i].d<0){
			suma++;
			tl[suma].d=e[i].d,tl[suma].w=e[i].w,tl[suma].x=e[i].x;
			tl[suma].tim=e[i].x;
		}
	}
	for(int i=1;i<=suma;i++){
		e[i].tim=tl[i].tim;
	}
	for(int i=suma+1;i<=n;i++){
		e[i].tim=tr[i-suma].tim;
	}
	sort(e+1,e+n+1,wht_cmp);
	for(int i=1;i<=n;i++){
		wht+=e[i].w;
		if(wht*2>=zt){
			fi_t=e[i].tim;
			break;
		}
	}
	for(int i=1;i<=sumb;i++){
		for(int j=1;j<=suma;j++){
			if(tl[j].x<tr[i].x) continue;
			if(tl[j].x-tr[i].x<=2*fi_t) ans++;
		}
		
	}
	cout<<ans;
	return 0;
} 

T4 抢粮食/P7990 [USACO21DEC] Closest Cow Wins S

懒得打了，代码里有注释，直接看吧（逃

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
const ll MAXN=2e5+10;
ll k,m,n,ans;
ll d[MAXN],impt[MAXN<<2],sum_impt;
struct cd{
	ll p,a;
	ll l,r;
}e[MAXN]; 
bool cmp(cd a,cd b){
	return a.p<b.p;
}
struct node{
	ll value,all,cnt;
	bool operator < (const node &a)const{
		return value<a.value;
	}
}ls;
priority_queue<node> q; 
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>k>>m>>n;
	for(ll i=1;i<=k;i++){
		cin>>e[i].p>>e[i].a;
	}
	for(ll i=1;i<=m;i++)
		cin>>d[i];
	sort(e+1,e+k+1,cmp);
	sort(d+1,d+m+1);//将（粮仓 or 草地）、（士兵 or 奶牛） 的坐标排序方便后续操作 
	ll all=0,nxt=1;
	while(nxt<=k&&e[nxt].p<d[1]){//对于最左边已经占用位置左边部分的所有草地，都只需要一个奶牛就可以获得全部价值 
		all+=e[nxt].a;
		nxt++;
	}
	ls.all=ls.value=all,ls.cnt=0;//一个奶牛的价值等于全部的价值 
	q.push(ls);
	for(int i=2;i<=m;i++){
		//枚举区间，对于当前占用位置和上一个占用位置之间的草地区间分别计算可以获得的价值 
		all=sum_impt=0;//sum_impt 区间关键点的个数，即非左右区间的草地半径点 
		ll lj=d[i-1],rj=d[i],fm=nxt;//fm 第一个草地 更新后的nxt为区间最后的草地 
		while(nxt<=k&&e[nxt].p<rj){
			int r=min(e[nxt].p-lj,rj-e[nxt].p);//草地半径，在半径以内的位置摆放可以获得这个草地的价值 
			e[nxt].l=e[nxt].p-r,e[nxt].r=e[nxt].p+r;//草地左右区间 （开区间）
			if(e[nxt].l!=lj) impt[++sum_impt]=e[nxt].l;
			if(e[nxt].r!=rj) impt[++sum_impt]=e[nxt].r;//更新关键点 
			all+=e[nxt].a,nxt++;//区间总价值 
		}
		if(fm==nxt) continue;//nxt未更新，这一块没有草，不用考虑
		impt[++sum_impt]=rj;//这里统一考虑在关键点左侧视为无限小距离放置，所以更新右边界未关键点 
		sort(impt+1,impt+sum_impt+1); 
		ll vl=0,tl=fm,tr=fm-1,w=0;//vl 为在这片草地上放置一个奶牛可以去得的最大价值
		//用类似区间伸缩的方式求得一个奶牛最大覆盖的草地区间 
		for(int j=1;j<=sum_impt;j++){//只有关键点能改变状态 
			ll dian=impt[j];
			while(tr+1<nxt&&dian>e[tr+1].l){
			//如果移动到的这个关键点大于当前可以达到最右边草地的左区间，就可以控制这个草地，那么更新右边界和答案 
				tr++;
				w+=e[tr].a;
			}	
			while(tl<nxt&&dian>e[tl].r){
			//同理，大于原先左边界的右区间，就无法获得原先左边界草地的价值，那么更新左边界，答案减少 
				w-=e[tl].a;
				tl++;
			}
			vl=max(vl,w);//每次更新统计获得的最大价值 
		}
		ls.all=all,ls.value=vl,ls.cnt=0;
		q.push(ls);
	}
	all=0;
	while(nxt<=k){
		all+=e[nxt].a;
		nxt++;
	}//与上同理，最右边占用位置的右边也只需要一个奶牛就可以获得全部价值 
	ls.all=ls.value=all,ls.cnt=0;
	q.push(ls);
	while(n&&!q.empty()){
		//每次取出区间用一个奶牛可以获得的最大价值，因为该区间最多需要两个奶牛可以获得全部价值，那么视为第二个奶牛的价值为总价值减去当前价值，记得儿更新标记 
		node tmp=q.top();q.pop();
//		cout<<tmp.all<<" "<<tmp.value<<" "<<tmp.cnt<<"\n";
		ans+=tmp.value;
		if(!tmp.cnt&&tmp.all!=tmp.value){
			tmp.cnt++;
			tmp.value=tmp.all-tmp.value;
			q.push(tmp);
		}
		n--;
	}
	cout<<ans;
	return 0;
}

前两道题好像也是usaco的题，但是找不到了（其实是懒得找

yqs怎么总是偷懒啊（恼