稀疏矩阵
本文主要围绕scipy中的稀疏矩阵展开,也会介绍几种scipy之外的稀疏矩阵的存储方式。
dok_matrix
继承自dict,key是(row,col)构成的二元组,value是非0元素。
优点:
- 非常高效地添加、删除、查找元素
- 转换成coo_matrix很快
缺点:
- 继承了dict的缺点,即内存开销大
- 不能有重复的(row,col)
适用场景:
- 加载数据文件时使用dok_matrix快速构建稀疏矩阵,然后转换成其他形式的稀疏矩阵
coo_matrix
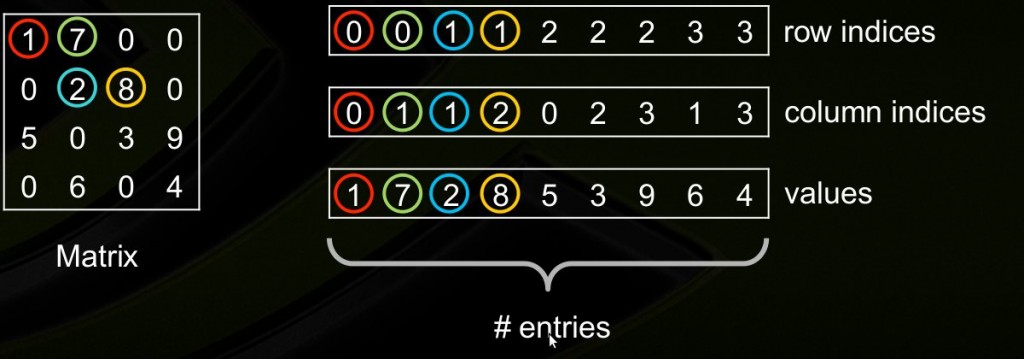
如上图,构造coo_matrix需要3个等长的数组,values数组存放矩阵中的非0元素,row indices存放非0元素的行坐标,column indices存放非0元素的列坐标。
优点:
- 容易构造
- 可以快速地转换成其他形式的稀疏矩阵
- 支持相同的(row,col)坐标上存放多个值
缺点:
- 构建完成后不允许再插入或删除元素
- 不能直接进行科学计算和切片操作
适用场景:
- 加载数据文件时使用coo_matrix快速构建稀疏矩阵,然后调用to_csr()、to_csc()、to_dense()把它转换成CSR或稠密矩阵
csr_matrix
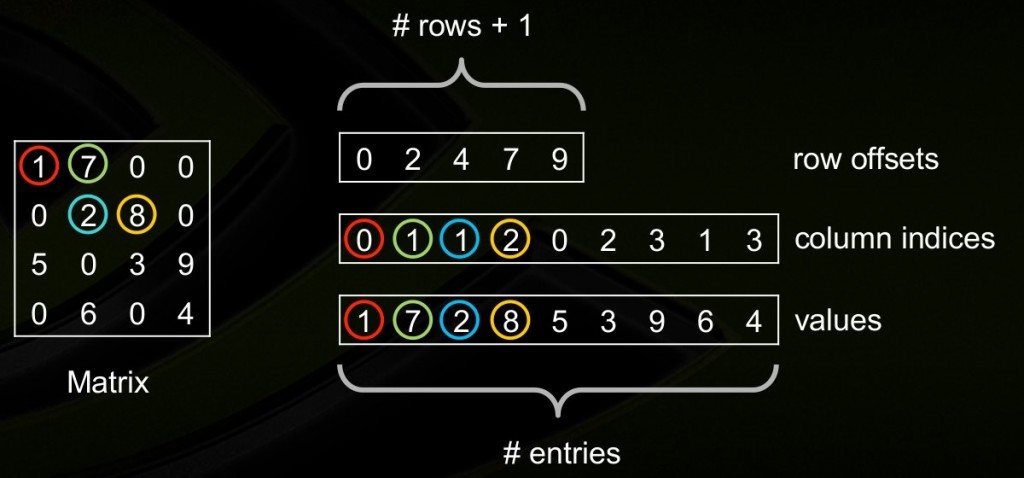
csr_matrix同样由3个数组组成,values存储非0元素,column indices存储非0元素的列坐标,row offsets依次存储每行的首元素在values中的坐标,如果某行全是0则对应的row offsets值为-1(我猜的)。
优点:
- 高效地按行切片
- 快速地计算矩阵与向量的内积
- 高效地进行矩阵的算术运行,CSR + CSR、CSR * CSR等
缺点:
- 按列切片很慢(考虑CSC)
- 一旦构建完成后,再往里面添加或删除元素成本很高
csc_matrix
跟csr_matrix刚好反过来。
bsr_matrix
跟CSR/CSC很相近,尤其适用于稀疏矩阵中包含稠密子矩阵的情况。在解决矢量值有限元离散(vector-valued finite element discretizations)这类问题中BSR比CSR/CSC更高效。
dia_matrix
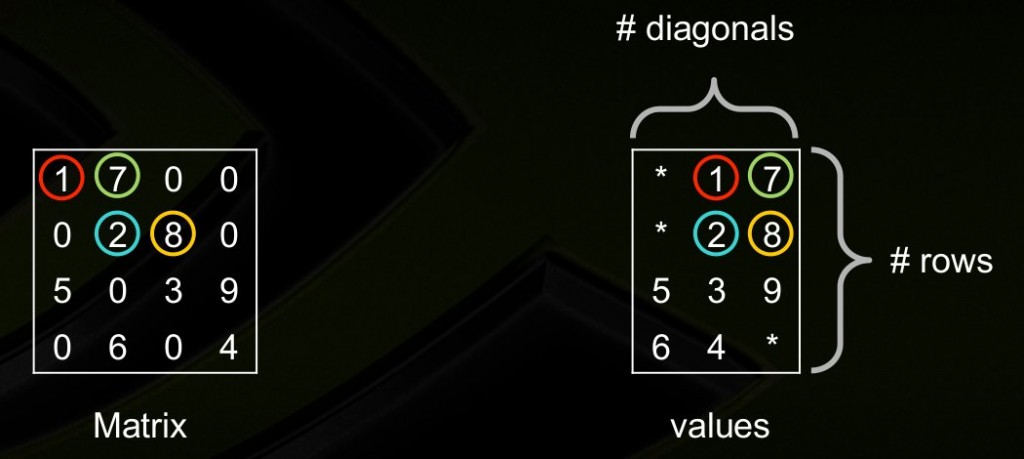
对角线存储法,按对角线方式存,列代表对角线,行代表行。省略全零的对角线。(从左下往右上开始:第一个对角线是零忽略,第二个对角线是5,6,第三个对角线是零忽略,第四个对角线是1,2,3,4,第五个对角线是7,8,9,第六第七个对角线忽略)。[3]
这里行对应行,所以5和6是分别在第三行第四行的,前面补上无效元素*。如果对角线中间有0,存的时候也需要补0。
适用场景:
- 如果原始矩阵就是一个对角性很好的矩阵那压缩率会非常高,比如下图,但是如果是随机的那效率会非常糟糕。
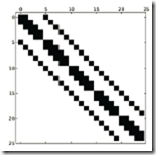
lil_matrix
内部结构是个二维数组:[[(col,value)]],第一行对应原矩阵的一行(可以快速地定位到行),行内按列编号排序好(通过折半查找可以快速地定位到列),同样只存储非0元素。
优点:
- 快速按行切片
- 高效地添加、删除、查找元素
缺点:
- 按列切片很慢(考虑CSC)
- 算术运算LIL+LIL很慢(考虑CSR或CSC)
- 矩阵和向量内和解很慢(考虑CSR或CSC)
适用场景:
- 加载数据文件时使用lil_matrix快速构建稀疏矩阵,然后调用to_csr()、to_csc()把它转换成CSR/CSC进行后续的矩阵运算
- 非0元素非常多时,考虑使用coo_matrix(我个人是这样理解的,lil_matrix用一个二维数组搞定,二维数组占用的是连续的内存空间,如果非0元素非常多就要申请一块非常大的连续的内存空间,这样性能很差。而coo_matrix毕竟是使用的3个一维数组,对连续内存空间的要求没那么高)
ELLPACK (ELL)
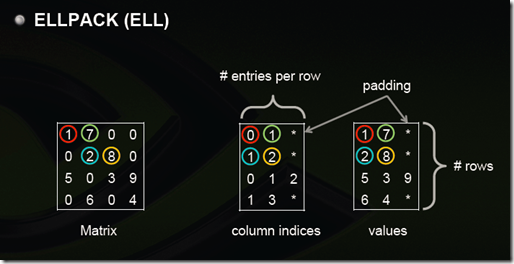
用两个和原始矩阵相同行数的矩阵来存:第一个矩阵存的是列号,第二个矩阵存的是数值,行号就不存了,用自身所在的行来表示;这两个矩阵每一行都是从头开始放,如果没有元素了就用个标志比如*结束。 上图中间矩阵有误,第三行应该是 0 2 3。
注:这样如果某一行很多元素,那么后面两个矩阵就会很胖,其他行结尾*很多,浪费。可以存成数组,比如上面两个矩阵就是:
0 1 * 1 2 * 0 2 3 * 1 3 *
1 7 * 2 8 * 5 3 9 * 6 4 *
但是这样要取一行就比较不方便了。
Hybrid (HYB) ELL + COO

为了解决ELL中提到的,如果某一行特别多,造成其他行的浪费,那么把这些多出来的元素(比如第三行的9,其他每一行最大都是2个元素)用COO单独存储。
skyline matrix storage
没看明白,自行wiki。
适用场景:
- 非常适合于稀疏矩阵的Cholesky分解或LU分解,这两种分解都是用来解线性方程组的。
行列双索引
这是自己实现的一种存储方式,分别按行和按列建立dict(dict中的key是行号或列号),这样按下标查找元素很快,但牺牲了空间。为了挽回空间上的牺牲,我们采用二进制来存储dict中的value。按下标查找元素时,根据行号定位到相应的value,value反序列化后转成dict,该dict的key是列号。
class DictMatrix():
'''用dict来实现稀疏矩阵
'''
def __init__(self, dft=0.0):
self._data = {}
self._dft = dft # “0元素”的值
self._nums = 0 # 稀疏矩阵中非0元素的个数
def __setitem__(self, index, value):
try:
i, j = index
except:
raise IndexError('invalid index')
# 为了节省内存,我们把j, value打包成字二进制字符串
ik = ('i%d' % i)
ib = struct.pack('if', j, value) # 格式化:i代替integer,f代表float。pack方法返回字符串
jk = ('j%d' % j)
jb = struct.pack('if', i, value)
try:
self._data[ik] += ib # 拼接字符串
except:
self._data[ik] = ib
try:
self._data[jk] += jb
except:
self._data[jk] = jb
self._nums += 1
def __getitem__(self, index):
try:
i, j = index
except:
raise IndexError('invalid index')
if (isinstance(i, int) and isinstance(j, int)):
ik = ('i%d' % i)
if self._data.has_key(ik):
ret = dict(np.fromstring(self._data[ik], dtype='i4,f4'))
return ret.get(j, self._dft)
else:
raise IndexError('invalid index')
return self._dft
def getRow(self, index):
'''获取某一行的数据,返回dict
'''
rect = dict()
if isinstance(index, int):
ik = ('i%d' % index)
if self._data.has_key(ik):
rect = dict(np.fromstring(self._data[ik], dtype='i4,f4'))
return rect
def getCol(self, index):
'''获取某一列的数据,返回dict
'''
rect = dict()
if isinstance(index, int):
jk = ('j%d' % index)
if self._data.has_key(jk):
rect = dict(np.fromstring(self._data[jk], dtype='i4,f4'))
return rect
def __len__(self):
return self._nums
def __iter__(self):
pass
def read(self, cache):
'''cache是一个list,其中的每个元素都是个三元组(row,col,value)。
从磁盘中加载稀疏矩阵时,可以先把部分数据加载到cache中,再从cache放到DictMatrix中。
'''
tmpDict = {}
for row, col, value in cache:
if value != self._dft: # 确保添加的是“非0”元素
ik = ('i%d' % row)
ib = struct.pack('if', col, value)
jk = ('j%d' % col)
jb = struct.pack('if', row, value)
try:
tmpDict[ik].write(ib)
except:
# 考虑到字符串拼接性能不太好,我们直接用StringIO的write()来做拼接
tmpDict[ik] = StringIO()
tmpDict[ik].write(ib)
try:
tmpDict[jk].write(jb)
except:
tmpDict[jk] = StringIO()
tmpDict[jk].write(jb)
self._nums += 1
for k, v in tmpDict.items():
v.seek(0)
s = v.read()
try:
self._data[k] += s
except:
self._data[k] = s
if __name__ == '__main__':
dtv = -1.0 # 默认值
matrix = DictMatrix(dtv)
matrix[1, 9] = 58.0
matrix[1, 16] = 20.0
matrix[2, 16] = 9
assert matrix[1, 10] == dtv # 元素不存在,取默认值
for k, v in matrix.getRow(1).items():
print k, v
for k, v in matrix.getCol(16).items():
print k, v
assert matrix[1, 9] == 58.0
assert matrix[1, 16] == 20.0
assert matrix[2, 16] == 9
assert matrix[2, 9] == dtv
print len(matrix)
matrix.read([(3, 3, 15), (9, 3, 100.0)]) # 批量添加数据
assert matrix[1, 9] == 58.0
assert matrix[3, 3] == 15
assert matrix[9, 3] == 100.0
print len(matrix)
上面的代码中做二进制序列化时用到了struck.pack,来个小例子看下序列化能省多少内存。
# coding=utf-8
__author__ = "orisun"
import struct
from cStringIO import StringIO
import numpy as np
from collections import defaultdict
loop1 = 10000
loop2 = 30
idx1 = 10
idx2 = 10
@profile
def foo1():
position_link = defaultdict(list) # list中每个元素是(int,float)类型的tuple
for i in xrange(loop1):
for j in xrange(loop2):
position_link[i].append((100000, 0.123435465))
print '1', position_link[idx1][idx2]
@profile
def foo2():
position_link = {}
for i in xrange(loop1):
tmp = StringIO()
for j in xrange(loop2):
# 使用StringIO的write()方法做二进制拼接,效率高一些
tmp.write(struct.pack('if', 100000, 0.123435465))
tmp.seek(0)
position_link[i] = tmp.read()
li = list(np.fromstring(position_link[idx1], dtype='i4,f4'))
print '2', li[idx2]
if __name__ == '__main__':
'''foo2比foo1节省16.7%的内存,但是慢了61.7%
使用memory_profiler查看内存使用
使用line_profiler查看耗时
'''
foo1()
foo2()
优点:
- 高效地动态添加元素
- 高效地按下标查找元素
- 高效地按行切片和按列切片
缺点:
- 不支持删除元素
- 内存占用略大
选择稀疏矩阵存储格式的经验
- DIA和ELL格式在进行稀疏矩阵-矢量乘积(sparse matrix-vector products)时效率最高,所以它们是应用迭代法(如共轭梯度法)解稀疏线性系统最快的格式
- COO格式常用于从文件中进行稀疏矩阵的读写,如matrix market即采用COO格式,而CSR格式常用于读入数据后进行稀疏矩阵计算
本文来自博客园,作者:张朝阳讲go语言,转载请注明原文链接:https://www.cnblogs.com/zhangchaoyang/articles/5483453.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号