PersonalRank：一种基于图的推荐算法

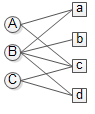
上面的二部图表示user A对item a和c感兴趣，B对a b c d都感兴趣，C对c和d感兴趣。本文假设每条边代表的感兴趣程度是一样的。

现在我们要为user A推荐item，实际上就是计算A对所有item的感兴趣程度。在personal rank算法中不区分user节点和item节点，这样一来问题就转化成：对节点A来说，节点A B C a b c d的重要度各是多少。重要度用PR来表示。

初始赋予 $PR(A)=1, PR(B)=PR(C)=PR(a)=PR(b)=PR(c)=PR(d)=0$，即对于A来说，他自身的重要度为满分，其他节点的重要度均为0。

然后开始在图上游走。每次都是从PR不为0的节点开始游走，往前走一步。继续游走的概率是$\alpha$，停留在当前节点的概率是$1-\alpha$。

第一次游走， 从A节点以各自50%的概率走到了a和c，这样a和c就分得了A的部分重要度，$PR(a)=PR(c)=\alpha*PR(A)*0.5$。最后$PR(A)$变为$1-\alpha$。第一次游走结束后PR不为0的节点有A a c。

第二次游走，分别从节点A a c开始，往前走一步。这样节点a分得A $\frac{1}{2}*\alpha$的重要度，节点c分得A $\frac{1}{2}*\alpha$的重要度，节点A分得a $\frac{1}{2}*\alpha$的重要度，节点A分得c $\frac{1}{3}*\alpha$的重要度，节点B分得a $\frac{1}{2}*\alpha$的重要度，节点B分得c $\frac{1}{3}*\alpha$的重要度，节点C分得c $\frac{1}{3}*\alpha$的重要度。最后$PR(A)$要加上$1-\alpha$

经过以上推演，可以概括成公式：

\begin{equation}PR(j)=\left\{\begin{matrix}\alpha*\sum_{i\in{in(j)}}\frac{PR(i)}{|out(i)|}\ \ \ \ if(j\ne{u})\\(1-\alpha)+\alpha*\sum_{i\in{in(j)}}\frac{PR(i)}{|out(i)|} \ \ \ \ if(j=u)\end{matrix}\right.\label{pr}\end{equation}

$u$是待推荐的用户节点。

personalrank.py

#coding=utf-8
__author__ = 'orisun'

import time


def PersonalRank(G, alpha, root, max_step):
    rank = dict()
    rank = {x:0 for x in G.keys()}
    rank[root] = 1
    #开始迭代
    begin=time.time()
    for k in range(max_step):
        tmp = {x:0 for x in G.keys()}
        #取节点i和它的出边尾节点集合ri
        for i, ri in G.items():
            #取节点i的出边的尾节点j以及边E(i,j)的权重wij, 边的权重都为1，归一化之后就上1/len(ri)
            for j, wij in ri.items():
                #i是j的其中一条入边的首节点，因此需要遍历图找到j的入边的首节点，
                #这个遍历过程就是此处的2层for循环，一次遍历就是一次游走
                tmp[j] += alpha * rank[i] / (1.0 * len(ri))
        #我们每次游走都是从root节点出发，因此root节点的权重需要加上(1 - alpha)
        tmp[root] += (1 - alpha)
        rank = tmp
    end=time.time()
    print 'use time', end - begin

    li = sorted(rank.items(), cmp=lambda x, y: cmp(x[1], y[1]), reverse=True)
    for ele in li:
        print "%s:%.3f, \t"%(ele[0], ele[1]),
    print
    
    return rank


if __name__ == '__main__' :
    alpha = 0.8
    G = {'A' : {'a' : 1, 'c' : 1},
         'B' : {'a' : 1, 'b' : 1, 'c':1, 'd':1},
         'C' : {'c' : 1, 'd' : 1},
         'a' : {'A' : 1, 'B' : 1},
         'b' : {'B' : 1},
         'c' : {'A' : 1, 'B' : 1, 'C':1},
         'd' : {'B' : 1, 'C' : 1}}

    PersonalRank(G, alpha, 'b', 50)     #从'b'节点开始游走

输出：

use time 0.00107598304749
B:0.312, b:0.262, c:0.115, a:0.089, d:0.089, A:0.066, C:0.066,

注意这里有一个现象，上述代码从节点b开始游走，最终算得的PR重要度最高的不是b，而是B。

personalrank经过多次的迭代游走，使得各节点的重要度趋于稳定，实际上我们根据状态转移矩阵，经过一次矩阵运算就可以直接得到系统的稳态。公式\eqref{pr}的矩阵表示形式为：

\begin{equation}r=(1-\alpha)r_0+\alpha{M^T}\label{mat}\end{equation}

其中$r$是个n维向量，每个元素代表一个节点的PR重要度，$r_0$也是个n维向量，第i个位置上是1，其余元素均为0，我们就是要为第i个节点进行推荐。$M$是n阶转移矩阵：

\begin{equation}M_{ij}=\left\{\begin{matrix}\frac{1}{|out(i)|}\ \ \ \ if(j\in{out(i)})\\0 \ \ \ \ else \end{matrix}\right.\end{equation}

按照矩阵乘法把\eqref{mat}展开就可以得到\eqref{pr}。

由\eqref{mat}可以得到两种变形：

\begin{equation}(I-\alpha{M^T})r=(1-\alpha)r_0\label{eq}\end{equation}

\begin{equation}r=(I-\alpha{M^T})^{-1}(1-\alpha)r_0\label{inv}\end{equation}

 利用\eqref{eq}，解一次线性方程组就查以得到$r$，对$r$中的各元素降序排列取出前K个就得到了节点i的推荐列表。实践中系数矩阵$(I-\alpha{M^T})$是一个高度稀疏的矩阵，解这种线性方程流行的方法是GMRES。另外在scipy中提供了多种稀疏矩阵的存储方法：coo,lil,dia,dok,csr,csc等，各有各的优缺点，dok可以快速的按下标访问元素，csr和csc适合做矩阵的加法、乘法运算，lil省内存且按下标访问元素也很快。更多内容参见scipy中的稀疏矩阵。

由于我们只关心$r$中各元素的相对大小，并不关心其真实值，所以\eqref{inv}可以写为

\begin{equation}r=(I-\alpha{M^T})^{-1}r_0\end{equation}

矩阵$(I-\alpha{M^T})^{-1}$乘以$r_0$相当于是取出矩阵的第i列，因此为节点i进行推荐时对矩阵$(I-\alpha{M^T})^{-1}$的第i列排序即可，所以求出矩阵$(I-\alpha{M^T})$的逆就得到了所有节点的推荐结果。

pr_matrix.py

# coding=utf-8
__author__ = 'orisun'

import numpy as np
from numpy.linalg import solve
import time
from scipy.sparse.linalg import gmres, lgmres
from scipy.sparse import csr_matrix

if __name__ == '__main__':
    alpha = 0.8
    vertex = ['A', 'B', 'C', 'a', 'b', 'c', 'd']
    M = np.matrix([[0,        0,        0,        0.5,    	0,        0.5,      0],
                   [0,        0,        0,        0.25,     0.25,     0.25,     0.25],
                   [0,        0,        0,        0,        0,        0.5,      0.5],
                   [0.5,	  0.5,    	0,        0,        0,        0,        0],
                   [0,        1.0,    	0,        0,        0,        0,        0],
                   [0.333,    0.333,    0.333,    0,        0,        0,        0],
                   [0,        0.5,    	0.5,      0,        0,        0,        0]])
    # print np.eye(n) - alpha * M.T
    r0 = np.matrix([[0], [0], [0], [0], [1], [0], [0]])  # 从'b'节点开始游走
    n = M.shape[0]

    # 直接解线性方程法
    A = np.eye(n) - alpha * M.T
    b = (1 - alpha) * r0
    begin = time.time()
    r = solve(A, b)
    end = time.time()
    print 'use time', end - begin
    rank = {}
    for j in xrange(n):
        rank[vertex[j]] = r[j]
    li = sorted(rank.items(), cmp=lambda x, y: cmp(x[1], y[1]), reverse=True)
    for ele in li:
        print "%s:%.3f, \t" % (ele[0], ele[1]),
    print

    # 采用CSR法对稀疏矩阵进行压缩存储，然后解线性方程
    A =np.eye(n) - alpha * M.T
    b = (1 - alpha) * r0
    data = list()
    row_ind = list()
    col_ind = list()
    for row in xrange(n):
        for col in xrange(n):
            if(A[row, col] != 0):
                data.append(A[row, col])
                row_ind.append(row)
                col_ind.append(col)
    AA = csr_matrix((data, (row_ind, col_ind)), shape=(n, n))
    begin = time.time()
    # 系数矩阵很稀疏时采用gmres方法求解。解方程的速度比上面快了许多
    r = gmres(AA, b, tol=1e-08, maxiter=1)[0]
    # r = lgmres(AA, (1 - alpha) * r0, tol=1e-08,maxiter=1)[0]  #lgmres用来克服gmres有时候不收敛的问题，会在更少的迭代次数内收敛
    end = time.time()
    print 'use time', end - begin
    rank = {}
    for j in xrange(n):
        rank[vertex[j]] = r[j]
    li = sorted(rank.items(), cmp=lambda x, y: cmp(x[1], y[1]), reverse=True)
    for ele in li:
        print "%s:%.3f, \t" % (ele[0], ele[1]),
    print

    # 求逆矩阵法。跟gmres解方程的速度相当
    A = np.eye(n) - alpha * M.T
    b = (1 - alpha) * r0
    begin = time.time()
    r = A.I * b
    end = time.time()
    print 'use time', end - begin
    rank = {}
    for j in xrange(n):
        rank[vertex[j]] = r[j, 0]
    li = sorted(rank.items(), cmp=lambda x, y: cmp(x[1], y[1]), reverse=True)
    for ele in li:
        print "%s:%.3f, \t" % (ele[0], ele[1]),
    print

    # 实际上可以一次性计算出从任意节点开始游走的PersonalRank结果。从总体上看，这种方法是最快的
    A = np.eye(n) - alpha * M.T
    begin = time.time()
    D = A.I
    end = time.time()
    print 'use time', end - begin
    for j in xrange(n):
        print vertex[j] + "\t",
        score = {}
        total = 0.0  # 用于归一化
        for i in xrange(n):
            score[vertex[i]] = D[i, j]
            total += D[i, j]
        li = sorted(score.items(), cmp=lambda x,
                    y: cmp(x[1], y[1]), reverse=True)
        for ele in li:
            print "%s:%.3f, \t" % (ele[0], ele[1] / total),
        print

输出：

use time 7.60555267334e-05
B:0.312, b:0.262, c:0.115, d:0.089, a:0.089, C:0.066, A:0.066,
use time 0.000385999679565
B:0.312, b:0.262, c:0.115, a:0.089, d:0.089, A:0.066, C:0.066,
use time 0.000133991241455
B:0.312, b:0.262, c:0.115, d:0.089, a:0.089, C:0.066, A:0.066,
use time 0.000274181365967
A A:0.314, c:0.189, B:0.166, a:0.159, C:0.076, d:0.063, b:0.033,
B B:0.390, c:0.144, d:0.111, a:0.111, C:0.083, A:0.083, b:0.078,
C C:0.314, c:0.189, B:0.166, d:0.159, A:0.076, a:0.063, b:0.033,
a a:0.308, B:0.222, A:0.159, c:0.133, d:0.070, C:0.063, b:0.044,
b B:0.312, b:0.262, c:0.115, d:0.089, a:0.089, C:0.066, A:0.066,
c c:0.340, B:0.192, C:0.126, A:0.126, d:0.089, a:0.089, b:0.038,
d d:0.308, B:0.222, C:0.159, c:0.133, a:0.070, A:0.063, b:0.044,