分治

分（divide）：递归解决较小的问题

治（conquer）：从子问题的解构建原问题的解

一般认为正文中至少含有两个递归调用才叫分治，只包含一个递归的不叫分治。一般认为子问题是不相交的。

方程 $T(N)=aT(N/b)+\Theta(N^k)$ 的解为：

整数相乘

求两个N位数X和Y的乘积，手算需要进行 $N^2$ 次乘法，即把两个个位数相乘看作基本操作的话，算法复杂度为 $O(N^2)$ 。X=12345678，Y=87654321，求XY。X_L=1234，X_R=5678，Y_L=8765，Y_R=4321。X=X_L10⁴+X_R，Y=Y_L10⁴+Y_R

所以：

$XY=X_LY_L10^8+(X_LY_R+X_RY_L)10^4+X_RY_R$

需要进行4次4位数的乘法 $4T(N/2)$ ，乘以10⁸只是一些补0操作，再加上几次加法构成了 $O(N)$ 。

$T(N)=4T(N/2)+O(N)$

由（1）式得 $T(N)=O(N^2)$ ，此时算法没有得到改进。

注意到 $X_LY_R+X_RY_L=(X_L-X_R)(Y_R-Y_L)+X_LY_L+X_RY_R$ ，所以在计算出 $X_LY_L\ X_RY_R$ 后，只需要再进行一次乘法就能计算出 $X_LY_R+X_RY_L$ 。

$T(N)=3T(N/2)+O(N)$

$T(N)=O(N^{log_2{3}})=O(N^{1.59})$

当两个数都是1位时可以通过查表进行乘法。

实际上上述方法在实际中很少用，对于小的N开销大，对于大的N还存在更好的一些算法，它们也广泛利用了分治算法。

矩阵乘法

$\parstyle\begin{eqnarray*}C_{11}=A_{11}B_{11}+A_{12}B_{21}\\C_{12}=A_{11}B_{12}+A_{12}B_{22}\\C_{21}=A_{21}B_{11}+A_{22}B_{21}\\C_{22}=A_{21}B_{12}+A_{22}B_{22}\end{eqnarray*}$

一个N×N的矩阵乘法变成了8个N/2×N/2的矩阵乘法和4个N/2×N/2的矩阵加法，加法的复杂度为 $O(N^2)$ 。

$T(N)=8T(N/2)+O(N^2)$

由（1）式得 $T(N)=O(N^3)$

看来矩阵分块后再进行乘积并没带来复杂度的降低。

Strassen使用了类似于整数乘法的分治策略。

　　计算7个N/2×N/2阶矩阵的乘法

$\mathbf{M}_{1} := (\mathbf{A}_{1,1} + \mathbf{A}_{2,2}) (\mathbf{B}_{1,1} + \mathbf{B}_{2,2})$

$\mathbf{M}_{2} := (\mathbf{A}_{2,1} + \mathbf{A}_{2,2}) \mathbf{B}_{1,1}$

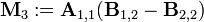
$\mathbf{M}_{3} := \mathbf{A}_{1,1} (\mathbf{B}_{1,2} - \mathbf{B}_{2,2})$

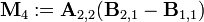
$\mathbf{M}_{4} := \mathbf{A}_{2,2} (\mathbf{B}_{2,1} - \mathbf{B}_{1,1})$

$\mathbf{M}_{5} := (\mathbf{A}_{1,1} + \mathbf{A}_{1,2}) \mathbf{B}_{2,2}$

$\mathbf{M}_{6} := (\mathbf{A}_{2,1} - \mathbf{A}_{1,1}) (\mathbf{B}_{1,1} + \mathbf{B}_{1,2})$

$\mathbf{M}_{7} := (\mathbf{A}_{1,2} - \mathbf{A}_{2,2}) (\mathbf{B}_{2,1} + \mathbf{B}_{2,2})$

然后

$\mathbf{C}_{1,1} = \mathbf{M}_{1} + \mathbf{M}_{4} - \mathbf{M}_{5} + \mathbf{M}_{7}$

$\mathbf{C}_{1,2} = \mathbf{M}_{3} + \mathbf{M}_{5}$

$\mathbf{C}_{2,1} = \mathbf{M}_{2} + \mathbf{M}_{4}$

$\mathbf{C}_{2,2} = \mathbf{M}_{1} - \mathbf{M}_{2} + \mathbf{M}_{3} + \mathbf{M}_{6}$

$T(N)=7T(N/2)+O(N^2)$

由（1）式得 $T(N)=O(N^{log_2{7}})=O(N^{2.81})$

当然要考虑N不是2的整次幂的情况。在N不是很大时Strassen算法不如矩阵直接相乘，它也不能推广到稀疏矩阵，而且不易并行化。当用浮点项运算时，在数值上不如经典算法稳定。算法稳定性是指：舍入误差在算法计算过程中是可控的。

posted @ 2012-09-07 19:12 张朝阳阅读(1519) 评论(2) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部