【机器学习】误差逆传播算法(反向传播算法)
误差逆传播算法(error BackPropagation,BP)是神经网络中常用的传播算法。BP算法不仅可以应用于多层前馈神经网络,还可以应用于其他类型的神经网络,如训练递归神经网络。通常所说的“BP网络”一般是指用BP算法训练的多层前馈神经网络。
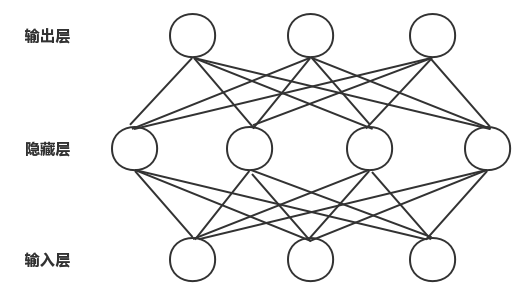
给定训练集 $ D=\left \{ (x_{1},y_{1}),(x_{2},y_{2}),..., (x_{m},y_{m})\right \},x_{i}\in \mathbb{R}^{d},y_{i}\in \mathbb{R}^{l} $ ,即输入由 $ d $ 个属性描述,输出 $ l $ 维实值向量。为便于讨论,给出有 $ d $ 个神经元、 $ l $ 个输出神经元、 $ q $ 个隐层神经元的多层前馈网络结构,其中输出层第 $ j $ 个神经元的阈值用 $ \theta _{j} $ 表示,隐层第 $ h $ 个神经元的阈值用 $ \gamma _{h} $ 表示。输入层第 $ i $ 个神经元与隐层第 $ h $ 个神经元之间的连接权重为 $ v_{ih} $ ,隐层第 $ h $ 个神经元与输出层第 $ j $ 个神经元之间的连接权重为 $ w_{ih} $ 。
记隐层第 $ h $ 个神经元接收到的输入为
$$
\begin{align}
\alpha _{h}=\sum_{i=1}^{d}v_{ih}x_{i}\nonumber
\end{align}
$$
输出层第 $ j $ 个神经元接收到的出入为
$$
\begin{align}
\beta _{j}=\sum_{h=1}^{q}w_{hj}b_{h}\nonumber
\end{align}
$$
其中 $ b_{h} $ 为隐层第 $ h $ 个神经元的输出。假设隐层和输出层的激活函数为Sigmoid函数。
对训练集 $ (x_{k}, y_{k}) $ ,假定神经网络的输出为
$$
\begin{align}
\hat y_{k}=\left (\hat y_{1}^{k}, \hat y_{2}^{k}, ..., \hat y_{l}^{k} \right )\nonumber
\end{align}
$$
即
$$
\begin{align}
\hat y_{l}^{k}=f\left ( \beta _{j}-\theta _{j} \right )
\end{align}
$$
则网络在 $ (x_{k}, y_{k}) $ 上的均方误差为
$$
\begin{align}
E_{k}=\frac{1}{2}\sum_{j=1}^{l}\left ( \hat y_{j}^{k}- y_{j}^{k} \right )^{2}
\end{align}
$$
网络中需要更新的参数个数为 $ \left ( d+l+1 \right )q+l $ 个:输入层到隐层的 $ d\times q $ 个权值、隐层到输出层的 $ q\times l $ 个权值、 $ q $ 个隐层神经元的阈值, $ l $ 个输出层神经元的阈值。BP是一个迭代学习算法,在迭代的每一轮中,采用广义的感知机学习规则对参数进行更新估计。对任意参数 $ v $ 的跟新估计为
$$
\begin{align}
v\leftarrow v+\Delta v\nonumber
\end{align}
$$
BP算法基于梯度下降策略,以目标的负梯度方向对参数进行调整,对式子(2)的 $ E_{k} $ ,给定学习率 $ \eta $ ,有
$$
\begin{align}
\Delta w_{hj}=-\eta \frac{\partial E_{k}}{\partial w_{hj}}
\end{align}
$$
注意到, $ w_{hj} $ 先影响到第 $ j $ 个输出层神经元的输入值 $ \beta _{j} $ ,再影响到其输出值 $ \hat y_{j}^{k} $ ,然后影响到 $ E_{k} $ ,有
$$
\begin{align}
\frac{\partial E_{k}}{\partial w_{hj}}=\frac{\partial E_{k}}{\partial \hat y_{j}^{k}}\cdot \frac{\partial \hat y_{j}^{k}}{\partial \beta _{j}}\cdot \frac{\partial \beta _{j}}{\partial w_{hj}}
\end{align}
$$
根据 $ \beta _{j} $ 定义,显然有:
$$
\begin{align}
b_{h}= \frac{\partial \beta _{j}}{\partial w_{hj}}{\partial w_{hj}}
\end{align}
$$
Sigmoid函数的导数为:
$$
\begin{align}
{f}'\left ( x \right )=f\left ( x \right )\left ( 1-f\left ( x \right ) \right )
\end{align}
$$
于是根据式子(1)和(2)有
$$
\begin{align}
g_{j} \nonumber
&=-\frac{\partial E_{k}}{\partial \hat y_{j}^{k}}\cdot \frac{\partial \hat y_{j}^{k}}{\partial \beta _{j}}\nonumber\\
&=-\left ( \hat y_{j}^{k}- y_{j}^{k}\right ){f}'\left ( \beta _{j}-\theta _{j} \right )\nonumber\\
&=\hat y_{j}^{k}\left ( 1- \hat y_{j}^{k}\right )\left ( y_{j}^{k} -\hat y_{j}^{k}\right )
\end{align}
$$
将式子 (5)、(7)带入式子(4),再带入式子(3)得到BP算法中关于 $ w_{hj} $ 的跟新公式:
$$
\begin{align}
\Delta w_{hj}=\eta g_{j}b_{h}
\end{align}
$$
类似地可以得到:
$$
\begin{align}
\theta _{j}=-\eta g_{j}
\end{align}
$$
$$
\begin{align}
v _{ih}=-\eta e_{h}x_{i}
\end{align}
$$
$$
\begin{align}
\gamma _{h}=-\eta e_{h}
\end{align}
$$
其中式子(10)、(11)中的 $ e_{h} $ 为,
$$
\begin{align}
e_{h}\nonumber
&=-\frac{\partial E_{k}}{\partial b_{h}}\cdot \frac{\partial b_{h}}{\partial \alpha _{h}}\nonumber\\
&=-\sum_{j=1}^{l}\frac{\partial E_{k}}{\partial \beta _{j}}\cdot \frac{\partial \beta _{j}}{\partial b_{h}}{f}'\left ( \alpha _{h}-\gamma _{h} \right )\nonumber\\
&=\sum_{j=1}^{l}w_{hj}g_{j}{f}'\left ( \alpha _{h}-\gamma _{h} \right )\nonumber\\
&=b_{h}\left ( 1- b_{h}\right )\sum_{j=1}^{l}w_{hj}g_{j}
\end{align}
$$
对于每一个训练样本,BP算法执行的步骤为:先将输入样本提供给输入层神经元,然后逐层将信号前传,指导产生输出层的结果;然后计算出输出层的误差,再将误差逆向传播到隐层神经元,最后根据隐层神经元的误差来对连接权重和阈值(偏量)进行调整。该过程为循环进行,直到满足某一过程为止。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号