多元线性回归-梯度下降法-吴恩达机器学习

0.工具

import copy, math, sys
import numpy as np

1.线性回归模型

def f_wb(x,w,b):
  return np.dot(w,x) + b

2.成本函数

def compute_cost(X, y, w, b):
  m,_ = X.shape
  J_wb = 0.0
  for i in range(m):
      J_wb += (f_wb(X[i],w,b) - y[i])**2
  J_wb /= 2*m

  return J_wb

3.梯度计算

def compute_gradient(X, y, w, b):
  m,n = X.shape
  dj_dw = np.zeros(n)
  dj_db = 0.0
  for i in range(m):
    err = f_wb(X[i],w,b) - y[i]
    for j in range(n):
      dj_dw[j] += err*X[i,j]
    dj_db += err
  for j in range(n):
    dj_dw[j] /= m
  dj_db /= m

  return dj_dw, dj_db

4.梯度下降法

def gradient_descend(X, y, w_init, b_init, alpha, num_iters):
  m,n = X.shape
  J_history = []
  p_history = []
  w = copy.deepcopy(w_init)
  b = b_init
  for t in range(num_iters):
    dj_dw, dj_db = compute_gradient(X, y, w, b)
    w_temp = w - alpha * dj_dw
    b_temp = b - alpha * dj_db
    w = w_temp
    b = b_temp
    
    J_history.append(compute_cost(X, y, w, b))
    
    if t% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {t:4d}: Cost {J_history[-1]:8.2f}   ")
  return w, b, J_history

5.测试算法正确性

X_train = np.array([[2104, 5, 1, 45], [1416, 3, 2, 40], [852, 2, 1, 35]])
y_train = np.array([460, 232, 178])
m,n = X_train.shape

w_initial = np.zeros(n)
b_initial = 0.0

iterations = 1000
alpha = 1e-7

w_final, b_final, J_hist = gradient_descend(X_train, y_train, w_initial, b_initial, alpha, iterations)

print(f"b,w found by gradient descent: {b_final:0.2f},{w_final} ")
for i in range(m):
    print(f"prediction: {np.dot(X_train[i], w_final) + b_final:0.2f}, target value: {y_train[i]}")

输出结果如下

Iteration    0: Cost 28989.11   
Iteration  100: Cost   696.86   
Iteration  200: Cost   696.65   
Iteration  300: Cost   696.43   
Iteration  400: Cost   696.21   
Iteration  500: Cost   696.00   
Iteration  600: Cost   695.78   
Iteration  700: Cost   695.57   
Iteration  800: Cost   695.36   
Iteration  900: Cost   695.14   
b,w found by gradient descent: -0.00,[ 0.20253263  0.00112386 -0.00213202 -0.00933401] 
prediction: 425.71, target value: 460
prediction: 286.41, target value: 232
prediction: 172.23, target value: 178

6.数据缩放

def zscore_normalize_features(X):
  mu = mean(X, axis = 0)
  sigma = std(X, axis = 0)
  X_norm = (X-mu)/sigma
  return X_norm, mu, sigma


X_norm, X_mu, X_sigma = zscore_normalize_features(X_train)
alpha = 0.1

w_final, b_final, J_hist = gradient_descend(X_norm, y_train, w_initial, b_initial, alpha, iterations)

输出如下，可以看到缩放处理数据后拟合结果好非常多

Iteration    0: Cost 37840.46   
Iteration  100: Cost     0.00   
Iteration  200: Cost     0.00   
Iteration  300: Cost     0.00   
Iteration  400: Cost     0.00   
Iteration  500: Cost     0.00   
Iteration  600: Cost     0.00   
Iteration  700: Cost     0.00   
Iteration  800: Cost     0.00   
Iteration  900: Cost     0.00   
b,w found by gradient descent: 290.00,[ 38.05161505  41.54327451 -30.98894656  36.34177447] 
prediction: 460.00, target value: 460
prediction: 232.00, target value: 232
prediction: 178.00, target value: 178

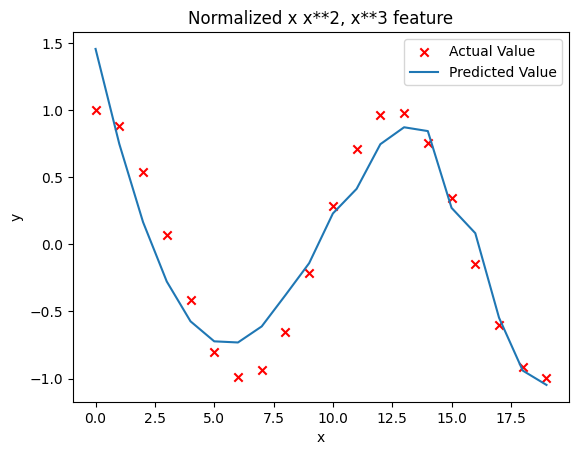
7.特征工程

x = np.arange(0,20,1)
y_train = np.cos(x/2)

X_train = np.c_[x, x**2, x**3,x**4, x**5, x**6, x**7, x**8, x**9, x**10]

w_final, b_final, J_hist = gradient_descend(X_norm, y_train, w_initial, b_initial, alpha, iterations)

使用十次多项式拟合余弦函数，结果如下