第01章 深度学习革命

概述: 利用机器从人类所创建的信息「语音、语言文字、图像」等载体中加速寻求出以前人类通过手工方式, 如经验、逻辑分析或实验才能获得的内在模式.

这好比显微镜或望远镜扩展了人类的视觉界限. 深度学习以逼近人脑的思维方式, 在拓展人脑的上限.

1. 影响

​ 图像信息: 医疗图像、蛋白质结构三维图像、用已有的图像寻找其内在模式来合成新的图像.

​ 语音信息: 在本章节中虽然并未举例, 语音合成技术「虚拟社交」如Soul

​ 文字信息: 大语言模型

​ 乍看三者似乎属于不同的领域, 但是它们如今都得以电子信息的方式储存, 每个领域都在人类的不懈努力下拆分出了它们的最小组成单元, 在线性空间里面即「基向量」, 给「基向量」添加不同的权重, 在同一领域下便可产生不同的效果.

​ 深度学习接近元学习. 我们人类现如今创造的信息只是对自然世界或人类世界的一种描述, 一个视角, 某个侧面. 放弃领域界限, 寻找领域之间的通用模式, 也是我们未来要走的路.

2. 拟合

一个简小的案例揭示机器学习的基本: 训练->获得模型->用模型应用于测试集->调参防过拟合优化->训练...

2.1 合成数据

​ 通过对sin(x) 添加随机噪声来合成数据.无论是训练集还是测试集都采用同样的模式合成.

%% 合成数据函数
% 输入参数 dt：采样率，默认值为1
% 输出参数 x, y：采样点和带噪声的正弦数据
% dt:默认1
% border: 默认10
function [x, y] = syntheticdata(dt, border)

    % 如果没有输入参数，设置默认采样率
    if nargin < 1
        dt = 1;
    end

    % 生成时间序列
    x = (0:dt:border)';     
    
    % 生成噪声，保证噪声幅度随采样率调整
    noise = randn(size(x)) * 0.1 * sqrt(dt); 
    
    % 生成带噪声的正弦信号
    y = sin(x) + noise;  

end

2.2 模型训练

​ 采样率为1, 合成11个数据, 得到训练集.

​ 借用Matlab自带的fit函数, 多项式拟合上述合成数据集.

%%  采用 Matlab默认的fit进行多项式拟合
% dt: 采样率
% border: 合成数据横轴边界
% M: [1:9] 模型阶数
function [wi, rms] = model(dt, border, M)
    %% 数据处理
    if nargin < 2
        dt = 1;  M = 9;
    end

    [x, y] = syntheticdata(dt, border); %合成训练集
    
    fs = cell(M, 1);      % 保存拟合多项式信息
    gof = cell(M, 1);     % 保存拟合优度信息
    for i = 1 : M
        [fs{i},gof{i}] = fit(x, y, ['poly' num2str(i)]);
    end
    


    % 多项式系数信息
    wi = zeros(M+1,M);    % 保存多项式系数
    for i = 1 : M
        for j = 1 : length(flip(coeffvalues(fs{i})))
            cof = flip(coeffvalues(fs{i}));
            wi(j, i) = cof(j);
        end
    end

    % 模型评估参数信息
    sse = zeros(M, 1);    % 残差平方和
    rms = zeros(M, 1);    % 均方根误差
    for i = 1 :  M
        sse(i) = gof{i}.sse;
        rms(i) = gof{i}.rmse;
    end

    %  寻找评估参数最小值对应的模型
    [minValueSSE, minIndexSSE] = min(sse);
    [minValueRMS, minIndexRMS] = min(rms);


    %% 绘图
    figure
    for i = 1 : M
        % 绘图
        subplot(3, 3, i);
        plot(fs{i}, x, y);
    
        ax = gca;
        ax.XAxisLocation = 'origin'; 
    
        ylim([-1.5, 1.5])
    
        title([' M = ' num2str(i) ', SSE = ' num2str(gof{i}.sse) ', RMS = ' num2str(gof{i}.rmse)], ...
            'FontSize', 10, 'FontWeight', 'bold', 'FontName', 'TimesRoman');
    
        legend off;
    end
    % 在整个figure底部添加文字
    annotation('textbox', [0 0 1 0.06], 'String', ...
        sprintf('最小残差平方和: M = %d, SSE = %.4f     最小均方根误差: M = %d, RMS = %.4f', ...
        minIndexSSE, minValueSSE, minIndexRMS, minValueRMS), ...
        'HorizontalAlignment', 'center', 'FontSize', 12, 'FontWeight', 'bold', ...
        'FontName', 'TimesRoman', 'EdgeColor', 'none');
    
    % 在整个figure顶部添加文字
    annotation('textbox', [0 0 1 0.99], 'String', ...
        sprintf('训练集: 多项式拟合'), ...
        'HorizontalAlignment', 'center', 'FontSize', 16, 'FontWeight', 'bold', ...
        'FontName', 'TimesRoman', 'EdgeColor', 'none');
    
    exportgraphics(gcf, './多项式拟合_训练.png', 'Resolution', 300);  % 高分辨率保存
end

​ 通过随机产生的噪声, 每次情况都不同, 截取单独一项作为分析.

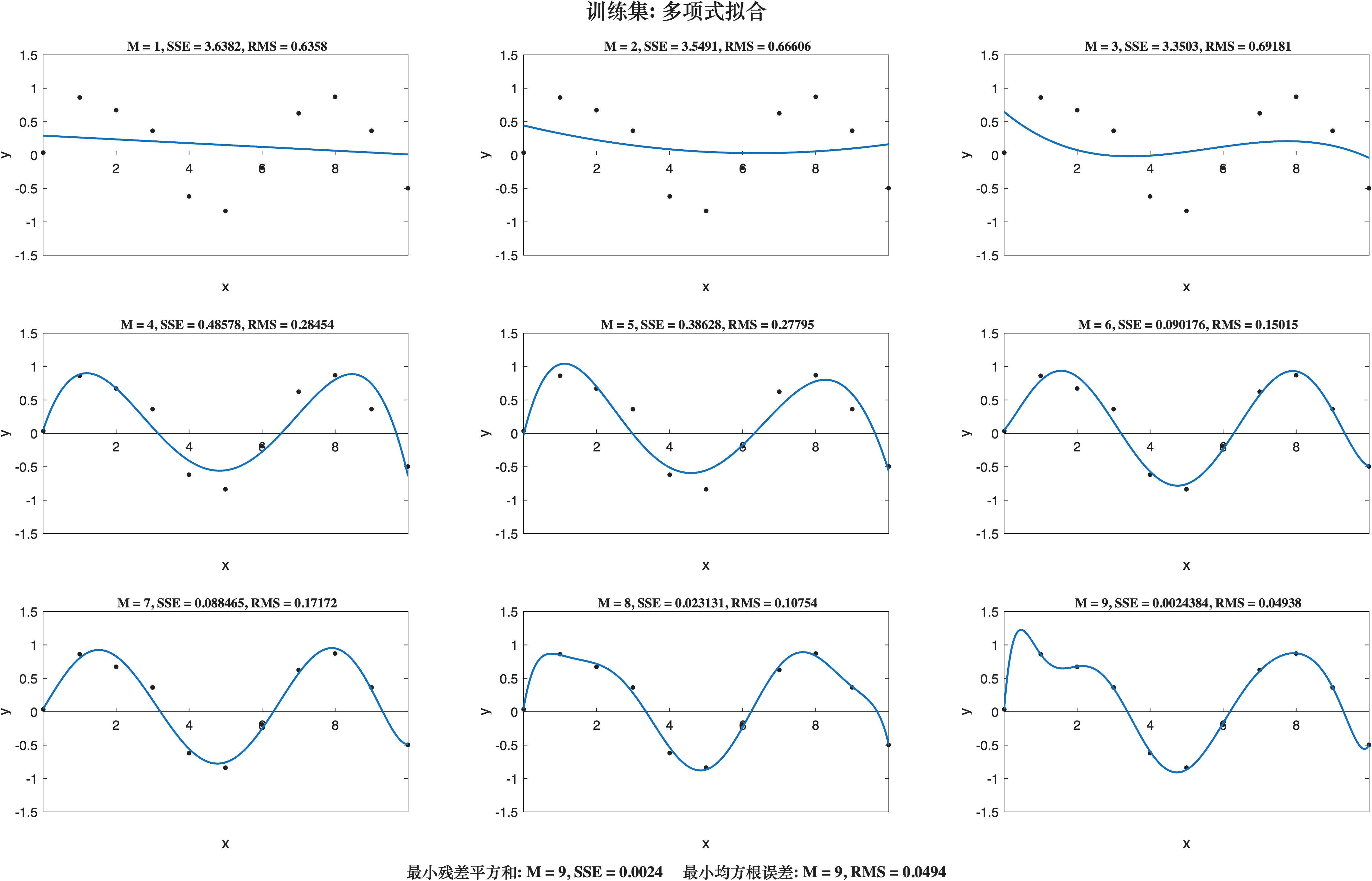
​ 上述的M 表示多项式阶数, 从成图上看, 当M=6时, 模型逼近sin(x) ; 当M=7时, 均方根误差增大; M=9虽然均方根很小, 将数据全部纳入了曲线中, 但是出现了过拟合 现象.

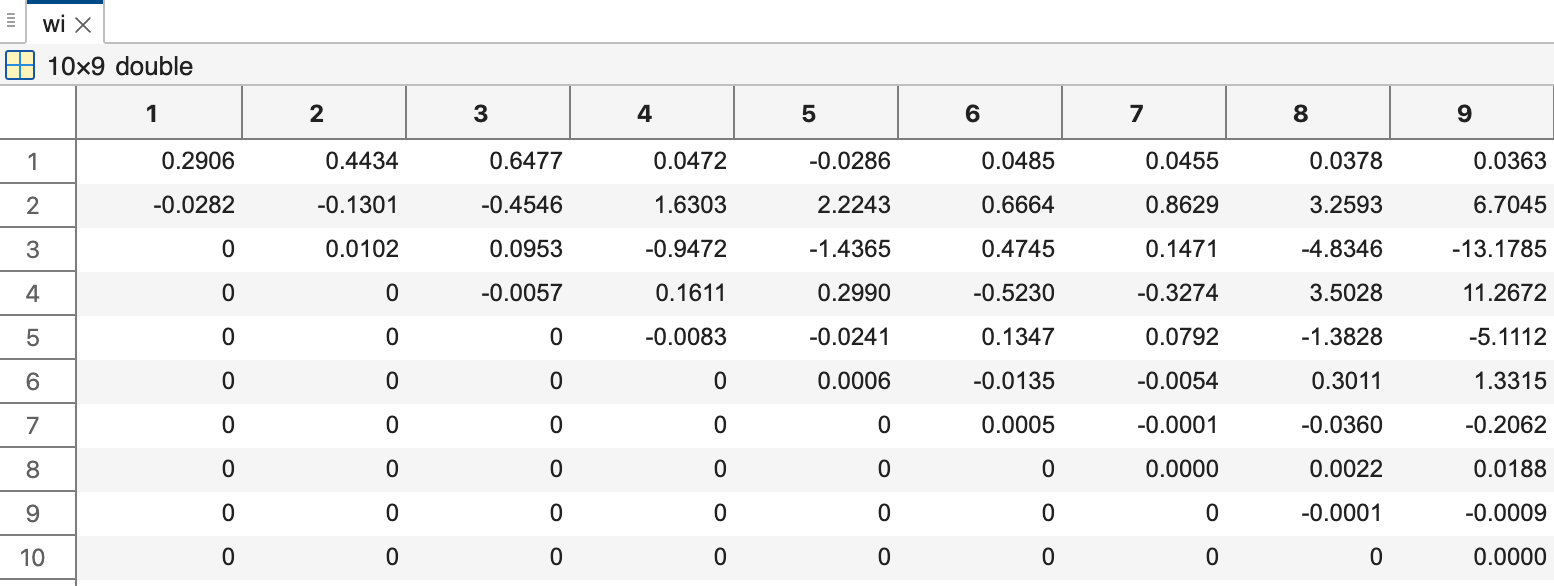
​ 我们从多项式系数可以观察到, 当M=8时, 系数值震荡的开始显著.当M=9时, 系数值震荡得更加厉害.
「奥卡姆剃刀原理」: 若有多个假设与观察一致, 则选最简单的那个.

2.3 预测数据

​ 采用率为0.1, 合成101个数据, 得到测试集.

​ 通过上述模型获得的系数应用于测试集.

% wi:  多项式模型权重系数
% rms: 模型均方根
% dt:  测试集采样率
% M:   多项式阶数「模型」
function test(border, wi, rms, dt, M)

    %% 数据处理
    [x, ytest] = syntheticdata(dt, border);%合成测试数据集
    
    % 利用模型预测
    n = length(x);
    V = zeros(n,M+1);     
    for k = 1:(M+1)
        V(:,k) = x.^(k-1);
    end
    ypre = V*wi; %利用训练模型预测数据结果

    % 评估参数SSE
    sse_errors = sum((ypre - ytest).^2, 1);  % 每列是一个模型的 SSE
    
    % 评估参数RMS
    rms_errors = zeros(9, 1);
    
    for i = 1 : M
        diff = ypre(:, i) - ytest;
        rms_errors(i) = sqrt(mean(diff .^ 2));     % RMS 计算
    end
    
    
    %% 绘制测试集预测图
    figure

    for i = 1 : M
    
        subplot(3, 3, i);
    
        % 测试数据用黑色实心圆点表示
        plot(x, ytest, 'ko', 'MarkerSize', 4, 'MarkerFaceColor', 'k', 'DisplayName', 'Test Data');
        hold on;
    
        % 模型预测用红色虚线
        plot(x, ypre(:, i), 'r--', 'LineWidth', 1.2, 'DisplayName', 'Model Prediction');
        hold off;
    
        ax = gca;
        ax.XAxisLocation = 'origin'; 
    
        ylim([-1.5, 1.5]);
    
        title([' M = ' num2str(i) ', SSE = ' num2str(sse_errors(i)) ', RMS = ' num2str(rms_errors(i))], ...
            'FontSize', 10, 'FontWeight', 'bold', 'FontName', 'TimesRoman');
        legend('Location', 'best');
    
    end
    
    
    % 在整个figure顶部添加文字
    annotation('textbox', [0 0 1 0.99], 'String', ...
        sprintf('测试集: 模型预测'), ...
        'HorizontalAlignment', 'center', 'FontSize', 16, 'FontWeight', 'bold', ...
        'FontName', 'TimesRoman', 'EdgeColor', 'none');
    exportgraphics(gcf, '多项式拟合_测试.png', 'Resolution', 300);  % 高分辨率保存


    %% 绘图
    figure
    x = [1:1:M];
    plot(x, rms_errors,'*-', 'DisplayName', '测试');
    hold on;
    plot(x, rms, '*-','DisplayName', '训练');
    legend('Location', 'best'); 

    title(['均方根误差图'],...
    'FontSize', 18, 'FontWeight', 'bold', 'FontName', 'TimesRoman');
    xlabel('M', 'Interpreter', 'latex', 'FontSize', 12, 'FontWeight', 'bold');
    ylabel('$E_{\mathrm{RMS}}$', 'Interpreter', 'latex', 'FontSize', 12, 'FontWeight', 'bold');
    exportgraphics(gcf, '均方根误差图.png', 'Resolution', 300);  % 高分辨率保存

end

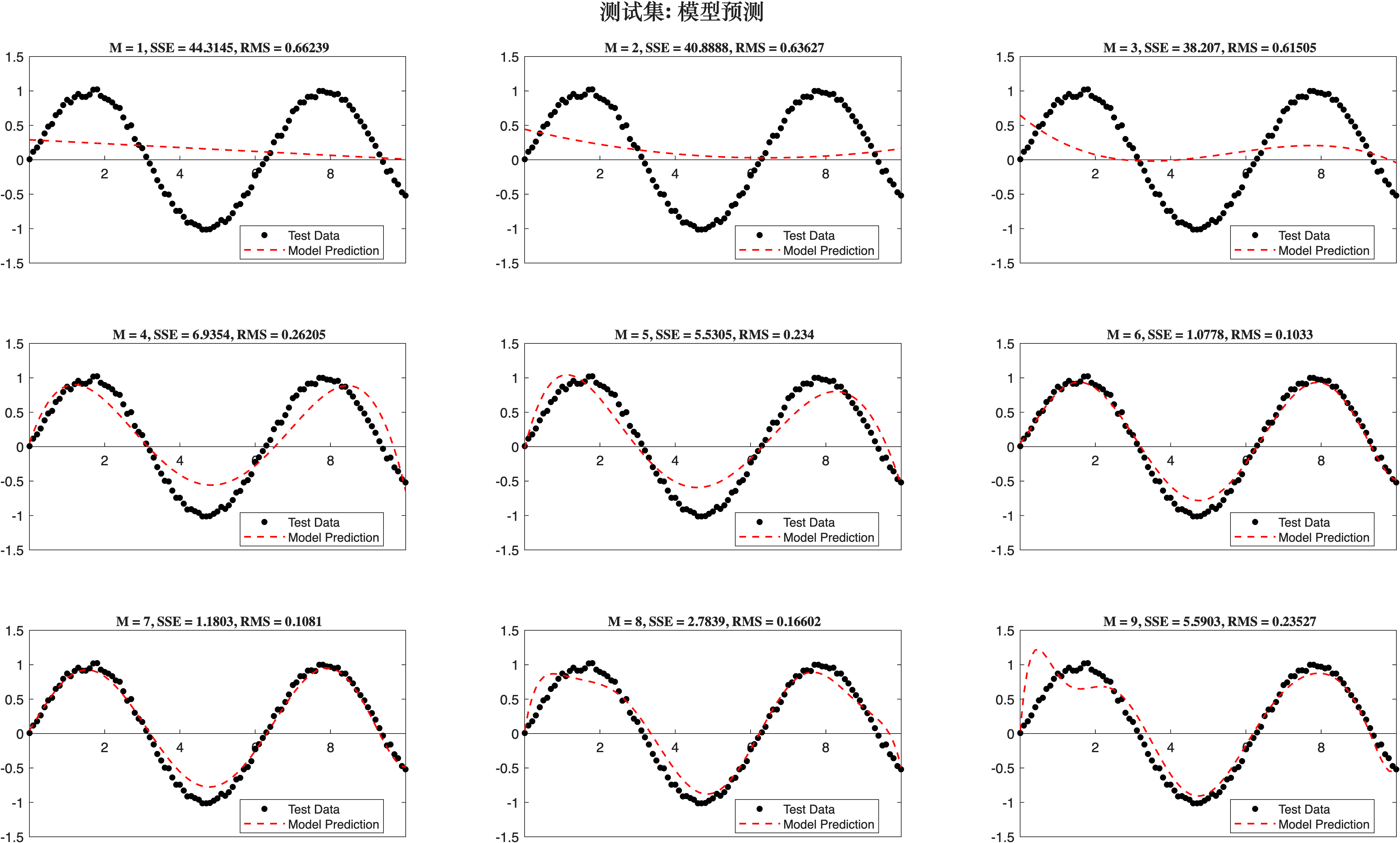
​ 尽管预测效果很粗糙, 却也显示出了sin(x) 的趋势.

​ 并且当M=6时与测试集数据的吻合度最好.在均方根误差图中我们也可以看到, M=6是对应参数处于最低点.

​ 当M>7之后,测试集所对应的RMS高于训练集.

2.4 正则化

利用最小二乘法拟合, 使用的岭回归进行正则化: Lambda越大, RMS越大.

%% 采用最小二乘法进行多项式拟合实验
% 
% dt:      采样率
% border:  横轴边界
% M:       最大阶数
% lambda:  正则化强度

function ridge_model(dt, x, y, M, lambda)

    if nargin < 4
        lambda = 0;  % 默认为无正则化（即普通最小二乘）
    end
    if nargin < 3
        M = 9;
    end

    % 构造Vandermonde矩阵（包括x^0常数项）
    N = length(x);
    V = zeros(N, M + 1);  % V(i,j) = x(i)^(j-1)
    for k = 1:(M + 1)
        V(:, k) = x.^(k - 1);
    end

    % 初始化输出
    W = zeros(M + 1, M);  % 每列是一个模型的权重
    rms = zeros(M, 1);    % 每个模型对应一个 RMS

    for i = 1:M
        Vi = V(:, 1:(i + 1));  % 使用阶数为 i 的模型

        % 岭回归闭式解：w = inv(VᵗV + λI) * Vᵗy
        I = eye(i + 1);
        w = (Vi' * Vi + lambda * I) \ (Vi' * y);

        % 保存系数（对齐在W前部）
        W(1:i + 1, i) = w;

        % 预测和误差计算
        yhat = Vi * w;
        rms(i) = sqrt(mean((yhat - y).^2));
    end

    % 绘图：训练集拟合曲线
    figure
    for i = 1:M
        subplot(3, 3, i);
        yhat = V(:, 1:(i+1)) * W(1:(i+1), i);
        plot(x, y, 'ko', 'MarkerSize', 4, 'MarkerFaceColor', 'k'); hold on;
        plot(x, yhat, 'LineWidth', 1.2); hold off;
        title(['M = ' num2str(i) ', RMS = ' num2str(rms(i))], ...
            'FontSize', 10, 'FontWeight', 'bold');
        ax = gca; ax.XAxisLocation = 'origin'; ylim([-1.5, 1.5]);
    end

    annotation('textbox', [0 0 1 0.99], 'String', ...
        sprintf('训练集: 多项式拟合 (λ = %.3f), dt = %.3f', lambda, dt), ...
        'HorizontalAlignment', 'center', 'FontSize', 16, ...
        'FontWeight', 'bold', 'EdgeColor', 'none',...
        'FontName', 'TimesRoman', 'EdgeColor', 'none');

    timestamp = datestr(now, 'HHMMSS');
    filename = ['figure_' timestamp '.png'];
    exportgraphics(gcf, filename, 'Resolution', 300);
    
end

% 正则化
[x, y] = syntheticdata(1, 10);
ridge_model(1, x, y, 9, 0.001);
ridge_model(1, x, y, 9, 0.01);
ridge_model(1, x, y, 9, 0.1);

[x, y] = syntheticdata(0.1, 10);
ridge_model(0.1, x, y, 9, 0.001);
ridge_model(0.1, x, y, 9, 0.01);
ridge_model(0.1, x, y, 9, 0.1);

采样率为1

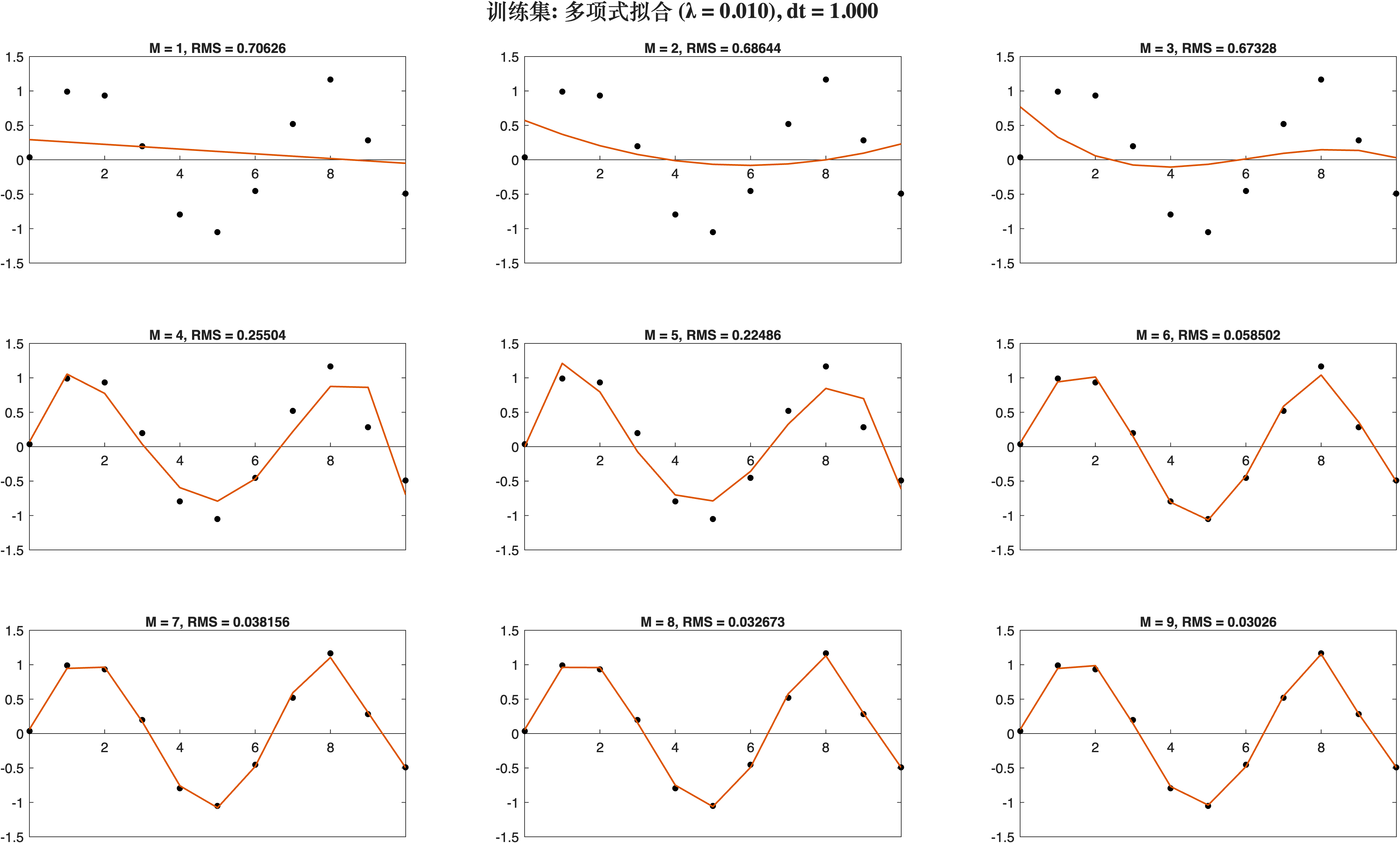
采样率为0.1

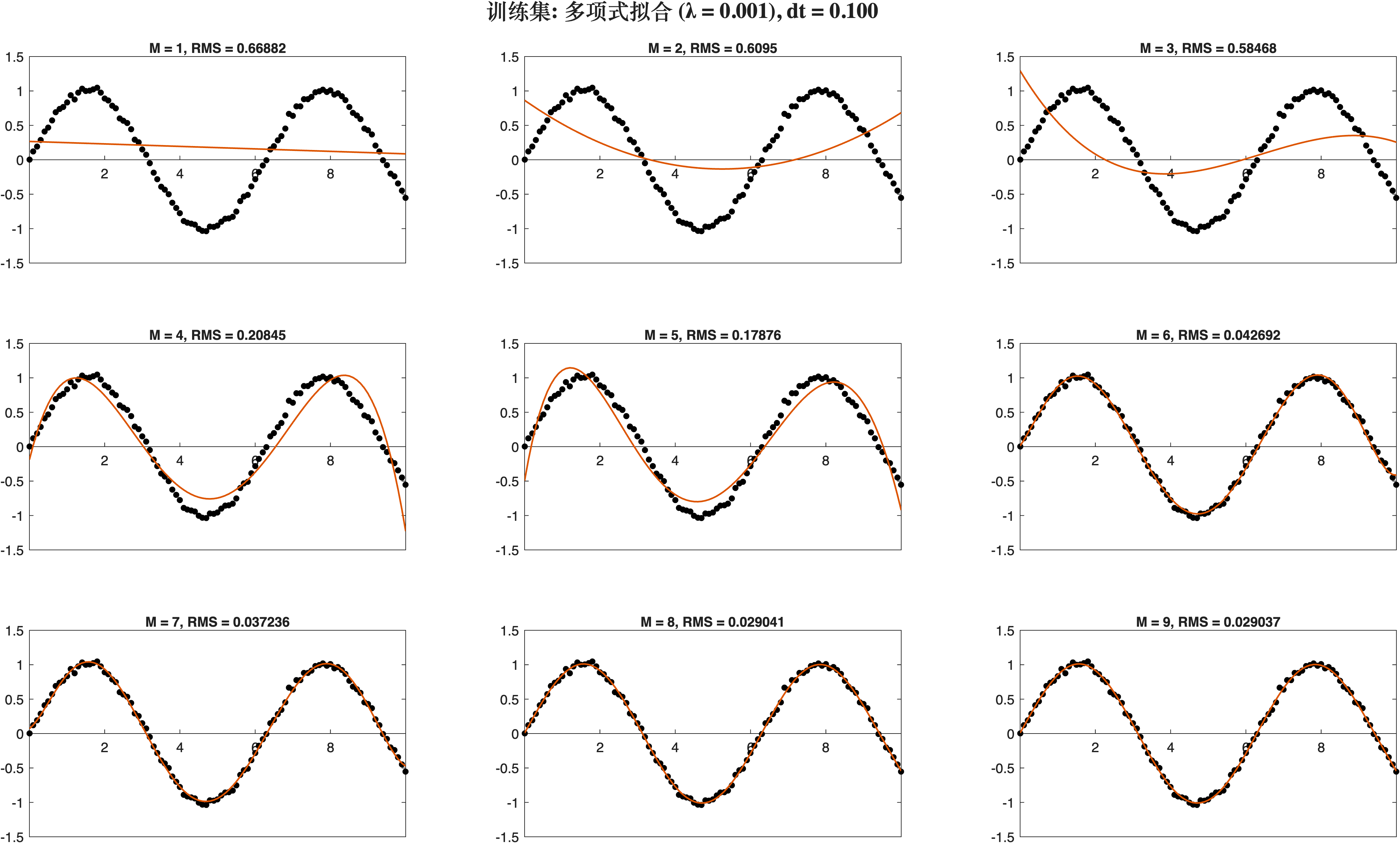
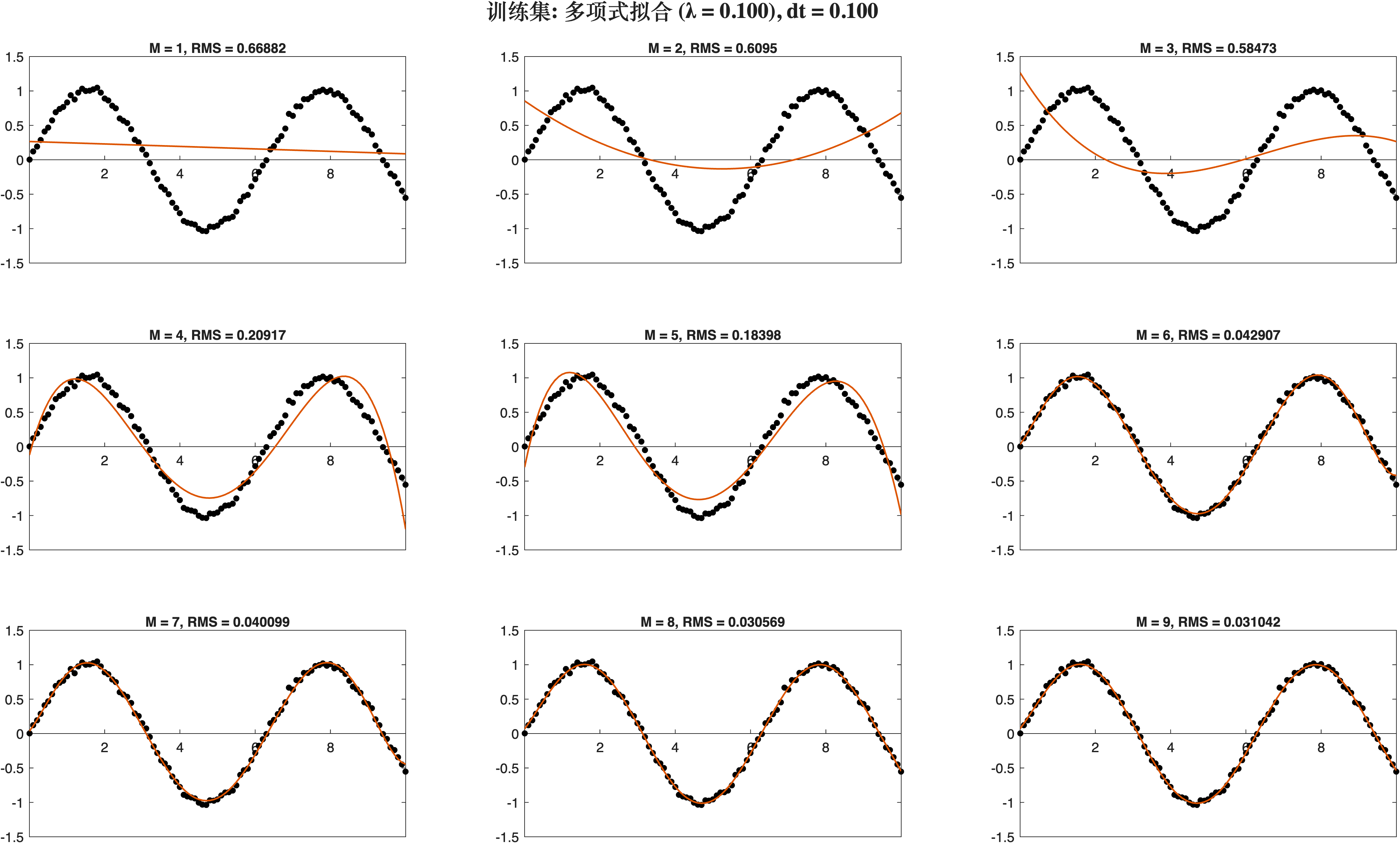
2.5 交叉验证

​ 将合成数据的border扩展成100, 增加10倍. 然后对合成数据进行切分标号.随机取一个作为测试集, 其他的每个都作为训练集找到最优的模型. 在此不做验证.

3. 历史

机器学习的发展符合涌现现象.它不仅是当下时代的产物.

​ 在大地测量学中, 有个误差传播理论. 当我们选取一个基准点进行测量, 因为测量精度关系, 每个测点都会存在一定的误差. 当下测点以前一个点为基准点, 就这样把内含的误差也携带过来.

​ 为了解决这个问题, 就需要进行校正的工作, 进行反推.

​ 当测点越多, 也就会变得愈加复杂.

​ 上述本质上是个线性问题. 但是从过程性质上来参考, 前向传播递推、反向传播矫正 、构建深层节点集. 可当「它山之石」, 辅助理解神经网络.