2024ICPC(杭州站)
A

首先判掉 \(|S_1|\ne |S_2|\) 和 \(|S_1|=|S_2|\ne |S_3|\) 的情况。
发现等价于给出了 \(\forall i,f(S_{1,i})=f(S_{2,i})\) 的限制。
判断是否 \(\exist i,f(S_{1,i})\ne f(S_{3,i})\)。
并查集。
K

我们肯定是将 \(k\) 次交换尽量用在同一行。
对每一行的数按涂色时间从小到大排序,必然将后 \(k\) 大移到前面,所以每一行答案就是 \(\max(m,第 k+1 大值涂色时间)\),若第 \(k+1\) 大值不存在就是 \(m\)。
最终答案对每行答案取 \(\min\) 即可。
E

首先考虑最小时间。
首先每个人需要的上升次数是固定的,为 \(\sum (r_i-l_i)\)。
其次我们必须要到达 \(r_{max}\),故还要加上 \(f\) 到 \(r_{max}\) 中没有区间覆盖的长度。
其次考虑构造。
首先到达 \(r_{max}\),每次找到一个满足 \(l\le f\) 且 \(r>f\) 的人,之后将这个人送过去一定不劣,如果找不到就只能走到 \(l>f\) 的最小的 \(l\) 所对应的人,答案加上 \(l-f\)。
其次从 \(r_{max}\) 按照终点先后顺序处理剩余的所有人,这样必定不会产生任何浪费。
指针+堆维护。
void solve() {
while(q.size()) q.pop();
cin>>n;int st=read();int mxr=0;
FOR(i,1,n) vis[i]=0,a[i]={read(),read(),i},cmax(mxr,a[i].y);
sort(a+1,a+n+1,cmp);
int j=0;LL ans=0;
vector<int>tmp;
while(1) {
if(st>=mxr) break;
while(j+1<=n&&a[j+1].x<=st) q.push({a[j+1].y,j+1}),++j;
if(q.size()&&q.top().fr>st) st=q.top().fr,vis[a[q.top().se].id]=1,tmp.eb(a[q.top().se].id),ans+=a[q.top().se].y-a[q.top().se].x,q.pop();
else {
if(j+1<=n) {
ans+=a[j+1].x-st;
st=a[j+1].x;
}
}
}
sort(a+1,a+n+1,cmp2);
ROF(i,n,1) {
if(vis[a[i].id]) continue;
tmp.eb(a[i].id);
ans+=a[i].y-a[i].x;
}
cout<<ans<<"\n";
for(int x:tmp) cout<<x<<" ";puts("");
}
H

清新构造。
首先如果只有一条链直接输出。
其次如果所有链长度相同或者最长链数量 \(\ge 2\) 且 最短链长度 \(=\) 最长链长度 \(-1\) 则无解。
对于最长链数量为 \(1\) 的情况,我们直接让其他所有链的父亲都设为最长链链顶即可,即最长链链顶为树根。
否则钦定一条最长链链顶为根,取出最短链,让它的链头父亲为最长链链头的儿子。
剩余的链头父亲设为根即可。
M

我们发现一个子数组的那个数必定是子数组的最小值。
建小根笛卡尔树,这样只需要对每个非根节点满足 \(a_{fa_x}+x|a_x+x\) 即可。
原式等价于
于是找到一个 \(a_x-a_{fa_x}\) 最小的位置将其所有约数枚举出并反解出 \(x\),之后对每个 \(x\) \(O(n)\) 判断就行了。
注意特判值全相等的情况。
复杂度 \(O(\sum\sqrt V+n d(V))\)。其中 \(d(i)\) 表示 \(1\sim i\) 中约数最多的数的约数个数。
F

首先对于每一个榜连边 \(p_i\to p_{i+1}\)。
跑 scc,发现一个榜上的 scc 一定是若干个区间。
而同一个 scc 中的任意两点都是好的。
查询一定是若干完整 scc 加上前后两个不完整 scc。二分与前缀和可做。
\(O(nk\log n)\)。
B

这个题值域 \(2^{63}\),想 \(n\log ^2 V\) 水过的可以洗洗睡了。
首先肯定是按位考虑,如果这一位在 \([l,r]\) 上只有 \(1\) 个 \(0\) 那么直接删。
考虑线段树,设 \(f_p\) 表示区间按位 \(\&\) 的结果,\(g_p\) 表示区间内只有 \(1\) 个 \(0\) 的位的位情况。
有 \(g_p=(g_{ls_p}\&f_{rs_p})|(g_{rs_p}\&f_{ls_p})\)。
单点修改有 \(g_p=\sim f_p\)。
区间 \(\&\) 要判断区间长度,如果是元区间要特判。
找到要删除的数字可以线段树上二分。
\(O((n+q)\log n)\)。
const int N=1e6+10,INF=LONG_LONG_MAX;
int n,q,f[N<<2],g[N<<2],tag[N<<2];
void Upt(int p,int l,int r,int v) {
f[p]&=v;tag[p]&=v;
if(l==r) g[p]=~f[p];
else g[p]&=v;
}
void push_down(int p,int l,int r) {
int mid=(l+r)>>1;
Upt(p<<1,l,mid,tag[p]);
Upt(p<<1|1,mid+1,r,tag[p]);
tag[p]=INF;
}
void change(int p,int l,int r,int x,int v) {
if(l==r) {
f[p]=v;g[p]=~v;
return ;
}
push_down(p,l,r);int mid=(l+r)>>1;
if(x<=mid) change(p<<1,l,mid,x,v);
else change(p<<1|1,mid+1,r,x,v);
f[p]=f[p<<1]&f[p<<1|1];
g[p]=(g[p<<1|1]&f[p<<1])|(f[p<<1|1]&g[p<<1]);
}
void And(int p,int l,int r,int ql,int qr,int v) {
if(ql<=l&&r<=qr) {
Upt(p,l,r,v);
return ;
}
int mid=(l+r)>>1;push_down(p,l,r);
if(ql<=mid) And(p<<1,l,mid,ql,qr,v);
if(qr>mid) And(p<<1|1,mid+1,r,ql,qr,v);
f[p]=f[p<<1]&f[p<<1|1];
g[p]=(g[p<<1|1]&f[p<<1])|(f[p<<1|1]&g[p<<1]);
}
pair<int,int> Merge(pair<int,int>l,pair<int,int>r) {
return {l.fr&r.fr,(l.fr&r.se)|(r.fr&l.se)};
}
pair<int,int> Askg(int p,int l,int r,int ql,int qr) {
if(ql>qr) return {INF,0};
if(ql<=l&&r<=qr) return {f[p],g[p]};
int mid=(l+r)>>1;push_down(p,l,r);
if(ql<=mid&&qr>mid) return Merge(Askg(p<<1,l,mid,ql,qr),Askg(p<<1|1,mid+1,r,ql,qr));
if(ql<=mid) return Askg(p<<1,l,mid,ql,qr);
return Askg(p<<1|1,mid+1,r,ql,qr);
}
int Ask(int p,int l,int r,int ql,int qr) {
if(ql>qr) return INF;
if(ql<=l&&r<=qr) return f[p];
int mid=(l+r)>>1,val=INF;push_down(p,l,r);
if(ql<=mid) val&=Ask(p<<1,l,mid,ql,qr);
if(qr>mid) val&=Ask(p<<1|1,mid+1,r,ql,qr);
return val;
}
int Find(int p,int l,int r,int ql,int qr,int bit) {
if(l==r) {
if(g[p]>>bit&1) return l;
return -1;
}
if(ql<=l&&r<=qr) {
int mid=(l+r)>>1;push_down(p,l,r);
if(g[p<<1]>>bit&1) return Find(p<<1,l,mid,ql,qr,bit);
if(g[p<<1|1]>>bit&1) return Find(p<<1|1,mid+1,r,ql,qr,bit);
return -1;
}
int mid=(l+r)>>1,pos=-1;push_down(p,l,r);
if(ql<=mid) pos=Find(p<<1,l,mid,ql,qr,bit);
if(~pos) return pos;
if(qr>mid) pos=Find(p<<1|1,mid+1,r,ql,qr,bit);
return pos;
}
main() {
cin>>n>>q;
fill(tag+1,tag+(n<<2)+1,INF);
FOR(i,1,n) {
int x=read();
change(1,1,n,i,x);
}
while(q--) {
int op=read(),l=read(),r=read(),x;
if(op==1) {
x=read();
And(1,1,n,l,r,x);
}
if(op==2) change(1,1,n,l,r);
if(op==3) {
auto pr=Askg(1,1,n,l,r);
if(!pr.se) {
printf("%lld\n",Ask(1,1,n,l,r));
continue;
}
int bt=__lg(pr.se);
int pos=Find(1,1,n,l,r,bt);
printf("%lld\n",Ask(1,1,n,l,pos-1)&Ask(1,1,n,pos+1,r));
}
}
return 0;
}
I

交互。
首先要通过询问距离在原环上尽量远的两个点使得这两个点的最短路 \(<n/2\),这个可以通过下述做法 \(O(1)\) 次查询做到。
-
令 \(u=n,v=(n+1)/2\)。
-
不断执行以下操作:
-
查询 \(u,v\) 距离,若 \(<n/2\) 直接退出。
-
如果 \(n\) 是偶数,令 \(u\gets u+1,v\gets v+1\)。
-
否则一开始令 \(u\gets u+1\),之后交替增加,这样可以保证不重不漏。
-
因为只有可能在 \(u,v\) 其中之一与弦的两端点距离分别为 \(x,y\) 且 \(|y-x|\le 1\) 时,才能使得最短路径不一定经过弦。而经过旋转 \(2\sim 3\) 次就可以破坏该条件。
我们找到距离 \(u\) 最近的弦的端点在 \(u\) 的哪一侧,这个直接查询 \(u+1,v\) 与 \(u-1,v\) 即可。
特别地如果两个条件都不满足说明 \(u\) 就是弦一端,啥都不干就行。
下面开始二分,这里以端点在 \(u+1\) 一侧为例。
上界为 \(0\),下界为 \(n/2\)。
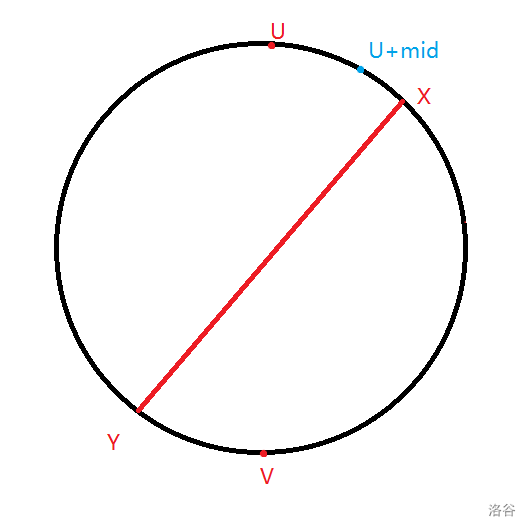
如果 \(dis(u+mid,v)=dis(u,v)-mid\),也即最短距离恰好能够缩 \(mid\),说明 \(x\) 在 \(u+mid\) 右边,故 \(l=mid+1\)。
由于 \(u,v\) 的最短路径必定是 \(u\to x\to y\to v\),故这是充要条件。
最终的 \(mid\) 表示弦的其中一个端点是 \(u+mid\)。
另一个端点也是好求的,必定有 \(v\) 与 \(y\) 的距离是 \(dis(x,v)-1\),直接判断即可。
使用 \(\log n+O(1)\) 次询问。
当然为了防止询问重复,可以用 map 存储询问过的点对。
void solve() { mp.clear();
cin>>n;
int st=n,ed=(n+1)/2,nw=1;
while(1) {
if(Ask(st,ed)<n/2) break;
if(n&1) nw?(st=nxt(st),nw^=1):(ed=nxt(ed),nw^=1);
else st=nxt(st),ed=nxt(ed);
}
int d=Ask(st,ed),pos=0,d1=Ask(pre(st),ed),d2=Ask(nxt(st),ed);
if(d1==d-1) {
int l=0,r=n/2;
while(l<=r) {
int mid=l+r>>1;
if(Ask(pr(st,mid),ed)==d-mid) {
pos=mid,l=mid+1;
} else r=mid-1;
}
st=pr(st,pos);
} else if(d2==d-1) {
int l=0,r=n/2;
while(l<=r) {
int mid=l+r>>1;
if(Ask(nt(st,mid),ed)==d-mid) {
pos=mid,l=mid+1;
} else r=mid-1;
}
st=nt(st,pos);
}
d=Ask(st,ed)-1;
int ps1=pr(ed,d),ps2=nt(ed,d);
if(Ask(ps1,st)==1) Puts(st,ps1);
else if(Ask(ps2,st)==1) Puts(st,ps2);
else Puts(st,ed);
return ;
}
J

设 \(S_1,S_2\) 表示第 \(1,2\) 个数组中出现的数字集合是什么。
知道这个后方案数为 \(C_{n_1-1}^{|S_1|-1}\times C_{n_2-1}^{|S_2|-1}\)。
显然以下三个条件与原题限制等价:
-
\(\forall i,a_i\in S_1\or b_i\in S_1\)
-
\(\forall i,a_i\in S_2\or b_i\in S_2\)
-
设 \(V=\bigcup \{a_i\}\cup \{b_i\}\),则 \(V\subseteq S_1\cup S_2\)
前两个条件独立,因此可以分别计算。
注意到第一个条件等价于 \(\nexists i,{a_i}\cup {b_i}\subseteq U\setminus S_1\)。
于是处理出 \(ok_S\) 表示 \(S\) 中是否存在这种 \(i\),这可以高维前缀或。
设 \(f_S\) 表示 \(S\) 的超集 \(T\) 中满足条件的 \(C_{n_1-1}^{|T|-1}\) 之和。
最终答案即:
\(f\) 可以高维后缀和。
复杂度 \(O(m2^m)\)。
void solve() {
cin>>n1>>n2>>m>>k;
int V=0;
FOR(i,1,k) {
int x=read()-1,y=read()-1;
V|=(1<<x)|(1<<y);
ok[(1<<x)|(1<<y)]=1;
}
FOR(i,0,m-1) FOR(S,0,(1<<m)-1)
if(S>>i&1) ok[S]|=ok[S^(1<<i)];
int Al=(1<<m)-1;
FOR(S,0,(1<<m)-1) if(!ok[Al^S]) f[S]=C(n1-1,(int)__builtin_popcount(S)-1);
FOR(i,0,m-1) FOR(S,0,(1<<m)-1)
if(!(S>>i&1)) (f[S]+=f[S|(1<<i)])%=Mo;
LL ans=0;
FOR(S,0,(1<<m)-1) if(!ok[Al^S]) (ans+=1LL*f[V^(S&V)]*C(n2-1,(int)__builtin_popcount(S)-1)%Mo)%=Mo;
cout<<ans<<"\n";
FOR(S,0,(1<<m)-1) f[S]=ok[S]=0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号