SAM&广义SAM

写的乱七八糟一塌糊涂我自己也看不懂千万千万不要尝试往下读坑还没有填迟早会填的希望我不要在填坑前退役

SAM

健忘症患者必备tmp。大佬博客

~~什么叫tmp，tmp就是垃圾记性不好一边看一边抄重点不然变成读议论文了。~~

对于一个字符串 S ，它对应的后缀自动机是一个最小的确定有限状态自动机（ DFA ），接受且只接受 S 的后缀。

定义

\(S=aabbabd\)

其中红色状态是终结状态。你可以发现对于S的后缀，我们都可以从S出发沿着字符标示的路径（蓝色实线）转移，最终到达终结状态。

特别的，对于S的子串，最终会到达一个合法状态。而对于其他不是S子串的字符串，最终会“无路可走”。

我们知道 SAM 本质上是一个 DFA ，DFA可以用一个五元组 <字符集、状态集、转移函数、起始状态、终结状态集> 来表示。至于那些绿色虚线虽然不是DFA的一部分，却是SAM的重要部分。

其中比较重要的是 状态集 和 转移函数 .

状态集

对于 S 的一个子串 s ，endpos(s)=s 在 S 中所有出现的结束位置集合。

性质

令 s1,s2 为 S 的两个子串，不妨设 |s1|≤|s2|

则 s1 是 s2 的后缀当且仅当 \(endpos(s1)⊇endpos(s2)\) ，

s1 不是 s2 的后缀当且仅当 \(endpos(s1)∩endpos(s2)=∅\)　。
SAM 中的一个状态包含的子串都具有相同的 endpos，它们都互为后缀。

其中一个状态指的是从起点开始到这个点的所有路径组成的子串的集合。

例如上图中状态 4 为 {bb,abb,aabb} 。
我们用 substrings(st) 表示状态 st 中包含的所有子串的集合，

longest(st)表示 st 包含的最长的子串，

shortest(st)表示st 包含的最短的子串。

那么有对于一个状态 st ，以及任意 s∈substrings(st) ，都有 s 是 longest(st) 的后缀。

证明比较容易，因为 \(endpos(s)=endpos(longest(st))\ |s|≤|st|\)，

所以 \(endpos(s)⊇endpos(longest(st))\) ，

根据我们刚才证明的结论有 s 是 longest(st) 的后缀。
对于一个状态 stst ，以及任意的 longest(st)的后缀 s ，

如果 s 的长度满足：|shortest(st)|≤|s|≤|longsest(st)| ，

那么 s∈substrings(st) 。

也就是说 substrings(st) 包含的是 longest(st) 的一系列连续后缀。

\(|shortest(st)| \le|s| \le |longsest(st)|\)，

所以 \(endpos(shortest(st)) ⊇ endpos(s) ⊇ endpos(longest(st))\) ，

又 \(endpos(shortest(st)) = endpos(longest(st))\) ，

所以 \(endpos(shortest(st)) = endpos(s) = endpos(longest(st))\) ，

所以 \(s\in substrings(st)\)

后缀链接

前面我们讲到 substrings(st) 包含的是 longest(st) 的一系列连续后缀。这连续的后缀在某个地方会“断掉”。

比如状态 7 ，

包含的子串依次是 aabbab,abbab,bbab,bab,aabbab,abbab,bbab,bab 。

按照连续的规律下一个子串应该是 ab ，但是 ab 没在状态 7 里。

原因：

aabbab,abbab,bbab,bab的 endposendpos 都是 {6} ，

下一个 ab 当然也在结束位置 66 出现过，但是 ab 还在结束位置 3 出现过，

所以 ab 比 aabbab,abbab,bbab,bab 出现次数更多，于是就被分配到一个新的状态中了。

当 longest(st) 的某个后缀 s 在新的位置出现时，就会“断掉”，s 会属于新的状态。

我们用后缀链接 SuffixLink 这一串状态链接起来，这条 link 就是上图中的绿色虚线。

转移函数

对于一个状态st，我们首先找到从它开始下一个遇到的字符可能是哪些。

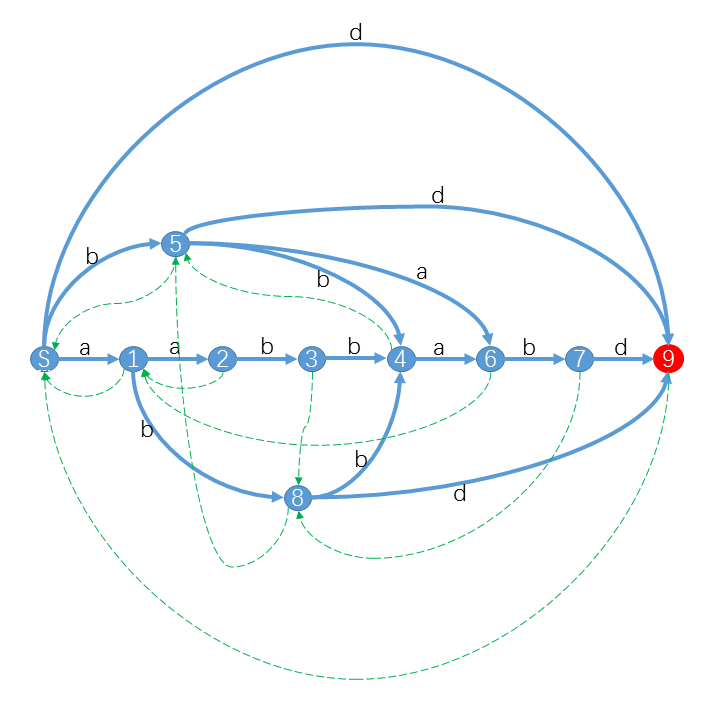
我们将 st 遇到的下一个字符集合记作 next(st) ，有\(next(st) = \{S[i+1] | i \in endpos(st)\}\) 。

例如 \(next(S)={S[1], S[2], S[3], S[4], S[5], S[6], S[7]}={a, b, d}\) ，\(next(8)={S[4], S[7]}={b, d}\) 。

算法构造

SAM 有 \(O(|S|)\) 构造方法。

对于状态 \(st\) 记录以下数据。

变量	含义
`maxlen[st]`	\(\|longest(st)\|\)
`minlen[st]`	\(\|shortest(st)\|\)
`trans[st][1..c]`	转移函数。\(c\) 为字符集大小
`link[st]`	\(st\) 的后缀链接

采用增量法构造SAM。

从初始状态开始，每次考虑添加一个字符 s[1],s[2],...s[N] ，依次构造可以识别 s[1..i] 的SAM。

假设已经构造好了 s[1..i] 的SAM，这时要添加字符 s[i+1] ，新增了 \(i+1\) 个后缀要识别。

这些状态分别是从 s[1..i],s[2..i]...s[i],空串 通过 s[i+1] 转移过来的。对它们对应状态添加相应转移。

假设 s[1..i] 对应状态为 \(u\) 等价于 s[1..i]\(\in sbstrings(u)\)

s[1..i],s[2..i]...s[i],空串 的状态是通过 \(u\) 到初始状态 \(S\) 之间的后缀链接连接起来的。

不妨称这条路径为 \(suffix-path(u\to S)\)

这个也就是说，对于 \(S[1..i]=longest(u)∈substrings(u)\)

对于其他 \(s′\) 为 \(longest(u)\) 的后缀要么存在于 \(u\) 这个状态中，要么存在于前面的 \(SuffixLink\) 连接的状态中。

显然至少 S[1..i+1] 这个子串不能被以前的 SAM 识别，所以我们至少需要添加一个状态 \(z\) ，\(z\) 至少包含 S[1..i+1] 这个子串。

情况1：

对于 suffix−path(u→S) 的任意状态 v ，都有 trans[v][S[i+1]]=NULL

这时我们只要令 trans[v][S[i+1]]=z ，并且令 link[st]=S 即可。
情况2：

suffix−path(u→S) 上有一个节点 v ，使得 trans[v][S[i+1]]≠NULL

suffix−path(u→S) 是橘色路径 4-5-S 。

对于状态 4 和状态 5 ，由于它们都没有对应字符 a 的转移，所以我们只要添加红色转移 trans[4][a]=trans[5][a]=z=6 即可。

但此时trans[S][a]=1 已经存在了。

不失一般性，我们可以认为在 suffix−path(u→S) 遇到的第一个状态 v 满足 trans[v][S[i+1]]=x 。

这时我们需要讨论 x 包含的子串的情况。
1. 如果 x 中包含的最长子串就是 v 中包含的最长子串接上字符 S[i+1] ，等价于maxlen(v)+1=maxlen(x)。
  
  这种情况比较简单，我们只要增加 link[z]=x 即可。与上图一样。
2. 如果 x 中包含的最长子串不是 v 中包含的最长子串接上字符 S[i+1] ，等价于 maxlen(v)+1<maxlen(x)，这种情况最为复杂。
  
  不失一般性，我们用下图表示这种情况，这时增加的字符是 c ，状态是 z 。
  
  在 suffix−path(u→S) 这条路径上，从 u 开始有一部分连续的状态满足 trans[u..][c]=NULL ，对于这部分状态我们只需增加 trans[u..][c]=z。
  
  紧接着有一部分连续的状态 v..w 满足trans[v..w][c]=x，并且 longest(v)+c 不等于 longest(x) 。
  
  这时我们需要从 x 拆分出新的状态 y ，并且把原来 x 中长度 \(\le\) longest(v)+c 的子串分给 y ，其余子串留给 x
  
  同时令 trans[v..w][c]=y ，link[y]=link[x] , link[x]=link[z]=y 。
  
  也就是 y 先继承 x 的 link ，并且 x,z 前面断开的 substrings 就存在于 y 中了。
  
  举个例子
  
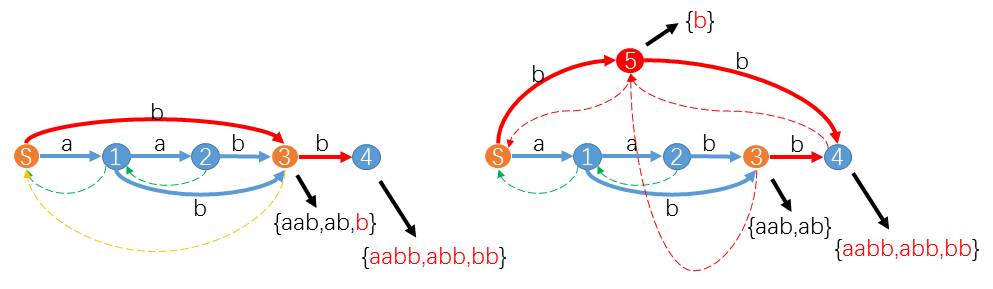
  当我们处理在 suffix−path(u→S) 上的状态 S 时，遇到 trans[S][b]=3 。并且 longest(3)=aab ，longest(S)+b ，两者不相等。
  
  其实不相等意味增加了新字符后 \(endpos(aab) \neq endpos(b)\) ，势必这两个子串不能同属一个状态 3 。
  
  这时我们就要从 3 中新拆分出一个状态 5 ，把 b 及其后缀分给 5 ，其余的子串留给 3 。
  
  同时令 trans[S][b]=5,link[5]=link[3]=S,link[3]=link[4]=5

~~累死我了~~

时间复杂度证明

状态个数：

结论：由长度为 n 的字符串 s 建立的后缀自动机的状态个数不超过 2n−1（对于 n≥3 ）。

证明：

上面描述的算法证明了这一性质（最初自动机包含一个初始节点，第一步和第二步都会添加一个状态，余下的 n−2 步每步由于需要分割，至多增加两个状态）。

所以就是 1+2+(n−2)×2=2n−1 了。

有趣的是，这一上限无法被改善，即存在达到这一上限的例子： abbb... 。每次添加都需要分割。

转移个数：

结论：由长度为 n 的字符串 s 建立的后缀自动机中，转移的数量不超过 \(3n−4\) （对于 n≥3 ）。

证明：

连续的转移个数

考虑以 S 为初始节点的自动机的最长路径树。这棵树将包含所有连续的转移，树的边数比结点个数小 1 ，这意味着连续的转移个数不超过 2n−2 。

不连续的转移个数

考虑每个不连续转移；假设该转移为转移 (p,q) ，标记为 c 。

对自动机运行一个合适的字符串 u+c+w ，其中字符串 u 表示从初始状态到 p 经过的最长路径，w 表示从 q 到任意终止节点经过的最长路径。

一方面，对所有不连续转移，字符串 u+c+w 都是不同的（因为字符串 u 和 w 仅包含连续转移）。

另一方面，每个这样的字符串 u+c+w ，由于在终止状态结束，它必然是完整串 s 的一个后缀。

由于 s 的非空后缀仅有 n 个，并且完整串 s 不能是某个 u+c+w （因为完整串 s 匹配一条包含 n 个连续转移的路径），那么不连续转移的总共个数不超过 n−1 。

有趣的是，仍然存在达到转移个数上限的数据：abbb...bbbc。

其实没太看懂。

代码实现

我们令 id 为这次插入字符的编号，trans,maxlen,linktrans,maxlen,link 意义同上。

Last 为上次最后插入的状态的编号，Size 为当前的状态总数，clone 为复制节点即上文的 y 。

具体来说如下代码所示：

minlen 可以最后计算，因为我们是从 link 处断开的，所以显然有 minlen[i]=maxlen[link[i]]+1 。

struct SAMSAM{
    int sz,lst;
    int maxlen[maxn<<1],trans[maxn<<1][26],link[maxn<<1];
    SAMSAM(){ sz=lst=1; }
    void extend(int c){
        int cur=(++sz),p;
        maxlen[cur]=maxlen[lst]+1;
        for(p=lst;p&&!trans[p][c];p=link[p]) trans[p][c]=cur;//最简单的情况
        if(!p) link[cur]=1;
        else {
            int q=trans[p][c];//有接c
            if(maxlen[q]==maxlen[p]+1) link[cur]=q;//=的可以直接link[cur]=q
            else {//最复杂的情况
                int cln=++sz;
                maxlen[cln]=maxlen[p]+1;
                for(int i=0;i<26;i++) trans[cln][i]=trans[q][i];
                link[cln]=link[q];
                for(;p&&trans[p][c]==q;p=link[p]) trans[p][c]=cln;//到q的trans
				//新建节点并继承信息

                link[cur]=link[q]=cln;
				//cur和q的link
            }
        }
        lst=cur;
    }
}SAM;

广义SAM

往往在两种题型以内。

令 \(G(T)\) 为 Trie 中所有叶节点深度之和，\(|T|\) 为trie大小。

多模式串问题：例如例题第三道，给出多个串，将串插入trie，再依靠这颗trie构造广义SAM。

\(G(T)=O(\sum len)=O(|T|)\)
直接给出trie：不常见。

\(G(T)=O(|T|^2)\)

离线构造

用所有模式串建出一个trie，对其 dfs/bfs 构建SAM 。

insert时使last为它在trie上的父亲，其余和普通SAM一样。

多模式串统计本质不同的子串个数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4e5+10,M=1e6+10;
int n,pos[M];
struct trietrie{
    int ch[M][27],cnt;
    trietrie(){ cnt=1; memset(ch,0,sizeof(ch)); }
    void ins(char* s){
        int len=strlen(s+1);
        int p=1;
        for(int i=1;i<=len;i++){
            int c=s[i]-'a';
            if(!ch[p][c]) ch[p][c]=++cnt;
            p=ch[p][c];
        }
        return;
    }
}trie;
struct SAMSAM{
    int sz;
    int trans[M<<1][27],link[M<<1],maxlen[M<<1];
    SAMSAM(){ sz=1; }
    int extend(int c,int lst){
        int cur=(++sz),p;
        maxlen[cur]=maxlen[lst]+1;
        for(p=lst;p&&!trans[p][c];p=link[p]) trans[p][c]=cur;
        if(!p) link[cur]=1;
        else {
            int q=trans[p][c];
            if(maxlen[q]==maxlen[p]+1) link[cur]=q;
            else {
                int cln=(++sz);
                maxlen[cln]=maxlen[p]+1;
                for(int i=0;i<26;i++) trans[cln][i]=trans[q][i];
                for(;p&&trans[p][c]==q;p=link[p]) trans[p][c]=cln;
                link[cln]=link[q]; link[cur]=link[q]=cln;
            }
        }
        return cur;
    }
    void dfs(int u){
        for(int i=0;i<26;i++){
            int v=trie.ch[u][i];
            if(v) pos[v]=extend(i,pos[u]),dfs(v);
        }
        return;
    }
    void build(){
        pos[1]=1; dfs(1); return;
    }
    void query(){
        ll res=0;
        for(int i=2;i<=sz;i++)
            res+=maxlen[i]-maxlen[link[i]];
        printf("%lld\n",res);
        return;
    }
}SAM;
int main(){
    char s[M];
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%s",s+1),trie.ins(s);
    SAM.build(); SAM.query();
    return 0;
}

在线构造

即不用提前构造出trie的做法。

在insert处做改动。

struct SAMSAM{
    int sz;
    int trans[M<<1][27],link[M<<1],maxlen[M<<1];
    SAMSAM(){ sz=1; }
    int extend(int c,int lst){
        int p,cln;
        if(trans[lst][c]){
            p=lst; int q=trans[p][c];
            if(maxlen[lst]+1==maxlen[q]) return q;//特判1
            else {
                cln=(++sz);
                maxlen[cln]=maxlen[p]+1;
                for(int i=0;i<26;i++) trans[cln][i]=trans[q][i];
                for(;p&&trans[p][c]==q;p=link[p]) trans[p][c]=cln;
                link[cln]=link[q]; link[q]=cln;
                return cln;//特判2
            }
        }
        int cur=(++sz);
        maxlen[cur]=maxlen[lst]+1;
        for(p=lst;p&&!trans[p][c];p=link[p]) trans[p][c]=cur;
        if(!p) link[cur]=1;
        else {
            int q=trans[p][c];
            if(maxlen[q]==maxlen[p]+1) link[cur]=q;
            else {
                cln=(++sz);
                maxlen[cln]=maxlen[p]+1;
                for(int i=0;i<26;i++) trans[cln][i]=trans[q][i];
                for(;p&&trans[p][c]==q;p=link[p]) trans[p][c]=cln;
                link[cln]=link[q]; link[cur]=link[q]=cln;
            }
        }
        return cur;
    }
    void ins(char* s){
        int nw=1,len=strlen(s+1);
        for(int i=1;i<=len;i++)
            nw=extend(s[i]-'a',nw);
        return;
    }
    void query(){
        ll res=0;
        for(int i=2;i<=sz;i++)
            res+=maxlen[i]-maxlen[link[i]];
        printf("%lld\n",res);
        return;
    }
}SAM;

例题

本质不同子串个数

统计所有状态包含的子串总数，也就是 \(\displaystyle \sum_{i=1}^{size} maxlen[i]-minlen[i]+1\) ，建完直接算就行了。

注意前面讲过的 minlen[i]=maxlen[link[i]]+1。

ll query(){
    ll ans=0;
    for(int i=1;i<=sz;i++){
        int minlen=maxlen[link[i]]+1;
        ans+=maxlen[i]-minlen+1;
    }
    return ans;
}

任意子串出现次数

求所有长度为 \(K\) 的子串中出现次数最多的子串的出现次数。\(k=1,2,3,...n\)

求任意子串出现次数：

显然一个子串出现次数是其 \(endpos\) 集合的大小。

但是暴力跳 \(suffix-path(u\to S)\) 总时间复杂度最高会达到 \(O(n^2)\)

发现所有的后缀链接建图后是一个DAG，拓扑\(dp\) 即可。注意 \(clone\) 不配拥有贡献。

回到本题，求所有长度为 \(K\) 的子串中出现次数最多的子串的出现次数。

\(K\in[minlen,maxlen]\)

对于每个节点，线段树一波即可。

但是这样太麻烦，显然对于长度更大时的ans一定 \(\ge\) 长度更小时的ans

所以直接把标记打在 \(maxlen\) 处然后倒回来就行。

\(O(n)\) 绝了。

艹，图建反了，调了一年。

void topo(){
    queue<int>q;
    for(int i=1;i<=sz;i++){
        if(!in[i]) q.push(i);
        if(vis[i]) f[i]=1;
    }
    while(!q.empty()){
        int u=q.front(); q.pop();
        ans[maxlen[u]]=max(ans[maxlen[u]],f[u]);
        for(int i=hd[u];i;i=nxt[i]){
            int v=to[i]; in[v]--;
            f[v]+=f[u];
            if(in[v]==0) q.push(v);
        }
    }
    for(int i=n-1;i>=1;i--) ans[i]=max(ans[i],ans[i+1]);
    return;
}
void query(){
    for(int i=1;i<=sz;i++)
        if(link[i]) add(i,link[i]);
    topo();
    for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
}

统计所有本质不同子串的权值和

\(n\) 个数串，统计所有字符串中的子串合在一起，求 \(sum=\) 本质不同字符串\(\times\)权值。 \(s\) 的权值 \(=\) \(s\) 直接作为数字

答案有可能很大，我们需要对 \(10^9 + 7\) 取摸。

艹，把空串算进去了，又调了一年。

广义SAM之后，直接拓扑DP即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10,M=1e6+10,mod=1e9+7;
int n,pos[M];
struct trietrie{
    int ch[M][27],cnt;
    trietrie(){ cnt=1; memset(ch,0,sizeof(ch)); }
    void ins(char* s){
        int len=strlen(s+1);
        int p=1;
        for(int i=1;i<=len;i++){
            int c=s[i]-'0';
            if(!ch[p][c]) ch[p][c]=++cnt;
            p=ch[p][c];
        }
        return;
    }
}trie;
struct SAMSAM{
    int sz;
    int trans[M<<1][11],link[M<<1],maxlen[M<<1];
    int in[M<<1],f[M<<1],dp[M<<1];
    bool vis[M<<1];
    SAMSAM(){ sz=1; }
    int extend(int c,int lst){
        int cur=(++sz),p; vis[cur]=1;
        maxlen[cur]=maxlen[lst]+1;
        for(p=lst;p&&!trans[p][c];p=link[p]) trans[p][c]=cur;
        if(!p) link[cur]=1;
        else {
            int q=trans[p][c];
            if(maxlen[q]==maxlen[p]+1) link[cur]=q;
            else {
                int cln=(++sz);
                maxlen[cln]=maxlen[p]+1;
                for(int i=0;i<10;i++) trans[cln][i]=trans[q][i];
                for(;p&&trans[p][c]==q;p=link[p]) trans[p][c]=cln;
                link[cln]=link[q]; link[cur]=link[q]=cln;
            }
        }
        return cur;
    }
    void dfs(int u){
        for(int i=0;i<10;i++){
            int v=trie.ch[u][i];
            if(v) pos[v]=extend(i,pos[u]),dfs(v);
        }
        return;
    }
    void build(){ pos[1]=1; dfs(1); return; }
    void add(int a,int b){ in[b]++; }
    void topo(){
        queue<int>q; int res=0;
        for(int i=1;i<=sz;i++)
            for(int j=0;j<10;j++)
                if(trans[i][j]) add(i,trans[i][j]);
        for(int i=1;i<=sz;i++){
        //    if(vis[i]) f[i]=1;
            if(!in[i]) q.push(i);
        }
        f[1]=1;
        while(!q.empty()){
            int u=q.front(); q.pop();
            res=(res+dp[u])%mod; //cout<<u<<" "<<f[u]<<" "<<dp[u]<<endl;
            for(int i=0;i<10;i++){
                int v=trans[u][i];
                if(v){
                    in[v]--; 
                    f[v]=(f[v]+f[u])%mod;
                    dp[v]=(dp[v]+(1ll*dp[u]*10%mod+1ll*i*f[u]%mod)%mod)%mod;
                    if(!in[v]) q.push(v);
                }
            }
        }
        printf("%d\n",(res+mod)%mod);
        return;
    }
    void query(){
        topo();
        return;
    }
}SAM;

也有不用广义SAM的做法。在两个串中间加上: 然后就像一个串一样加入，在拓扑dp的时候，是: 出边的点不能计算答案也不加入拓扑。

求循环串在原串中的出现次数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10,M=1e6+10;
int n,m;
int sz,lst;
int siz[M<<1]; int vis[M<<1];
int trans[M<<1][27],maxlen[M<<1],link[M<<1];
int buc[M<<1],ord[M<<1];
int extend(int c){
    int cur=(++sz),p;
    maxlen[cur]=maxlen[lst]+1; siz[cur]=1;
    for(p=lst;p&&!trans[p][c];p=link[p]) trans[p][c]=cur;
    if(!p) link[cur]=1;
    else {
        int q=trans[p][c];
        if(maxlen[q]==maxlen[p]+1) link[cur]=q;
        else {
            int cln=(++sz);
            link[cln]=link[q]; maxlen[cln]=maxlen[p]+1;
            memcpy(trans[cln],trans[q],sizeof(trans[q]));

            for(;p&&trans[p][c]==q;p=link[p]) trans[p][c]=cln;
            link[cur]=link[q]=cln;
        } 
    }
    return lst=cur;
}
void topo(){
  //  for(int i=1;i<=sz;i++) cout<<siz[i]<<endl;
   // cout<<"****"<<endl;
    for(int i=1;i<=sz;i++) buc[maxlen[i]]++;
    for(int i=1;i<=sz;i++) buc[i]+=buc[i-1];
    for(int i=1;i<=sz;i++) ord[buc[maxlen[i]]--]=i;
    for(int i=sz,p;i>=1;i--) p=ord[i],siz[link[p]]+=siz[p];
    siz[1]=0;
    return;
}
ll query(char* s,int id){
    ll ans=0; m=strlen(s+1);
    for(int i=1;i<m;i++) s[m+i]=s[i];
    int tm=m; m=2*m-1;

    int p=1,l=0;
    for(int i=1;i<=m;i++){
        int c=s[i]-'a';
        if(trans[p][c]) p=trans[p][c],l++;
        else {
            while(p&&!trans[p][c]) p=link[p],l=maxlen[p];
            if(trans[p][c]) l=maxlen[p]+1,p=trans[p][c]; else p=1,l=0;
        }
        if(l>tm) while(maxlen[link[p]]>=tm) p=link[p],l=maxlen[p]; 
     //   cout<<i<<" "<<l<<" "<<p<<"*"<<siz[p]<<endl;
        if(l>=tm&&vis[p]!=id) ans+=siz[p],vis[p]=id;
    }
    return ans;
}
int main(){
    char s[M<<1]; scanf("%s",s+1);
    n=strlen(s+1); sz=lst=1;
    memset(vis,-1,sizeof(vis));
    for(int i=1;i<=n;i++) extend(s[i]-'a');

    topo();
    int t; scanf("%d",&t);
    while(t--){
        scanf("%s",s+1);
        printf("%lld\n",query(s,t));
    }
    return 0;
}

posted @ 2021-01-09 07:41 ACwisher 阅读(76) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

下笔春蚕食叶声。

ACwisher

A little Vegetable Chicken