威佐夫博弈学习笔记。

早上起来 脑壳痛
太阳好白 头好重
脑子没带 身子先动
边出门 边做梦

威佐夫博弈。

有两堆石子和两个人，轮流操作：从两堆石子同时取走至少一颗，或者从某堆石子里取走至少一颗，先没法操作的人输，给出某个状态问是否先手必胜。

从知乎偷个图，建出坐标系之后发现必败点满足这个条件。

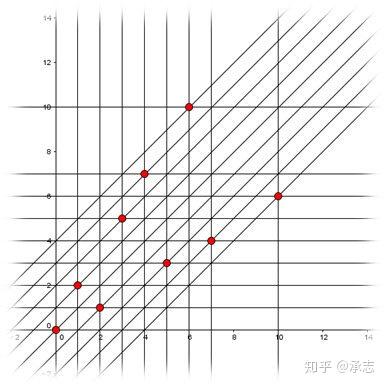
显然它关于 \(x=y\) 对称，所以我们只考虑 \(x\le y\) 的点。

列出来前几个点：\((0,0),(1,2),(3,5),(4,7),(6,10),(8,13),(9,15),(11,18),(12,20),(14,23),(16,26),(17,28),(19,31),(21,34),(22,36),(24,39)\)

注意到第 \(n\) 项满足 \(y-x=n\)。

然后我们还有若干性质：

• 一个必败点的决策不可能到达必败点。因为对于这个必败点如果可以走向必败点，直接走过去会使得对方必败，也就是必胜点。所以每对必败必胜点的两个坐标一定不同，两个坐标的差值一定不同。
• 如果一个点的决策里没有必败点，那它是必败点。因为只有走向必败点才能让对方必败而自己必胜。
• 每个 \(x_i=\operatorname{mex}_{j=0}^{i-1}(x_j,y_j),y_i=x_i+i\)。考虑归纳证明法，假如升序排序前 \(i-1\) 项都满足 \(x_i+i=y_i\)，那么接下来满足 \(x\) 最小的值肯定为前面所有数的 \(\operatorname{mex}\)，而满足两位差没有出现过的最小值为 \(i\)，并且因为 \(x,y\) 都单调递增，所以这个 \(y=x+i\) 肯定没出现过。

然后我们考虑通项公式，有一个定理如下。

Betty 定理

如果两个无理数 \(a,b\) 满足 \(\frac{1}{a}+\frac{1}{b}=1\)，那么对于集合 \(A=\big\{\lfloor n\times a\rfloor\big\},B=\big\{\lfloor m\times b\rfloor\big\}(n,m\in \mathbb{N}^+)\)，有 \(A\cup B=\mathbb{N}^+,A\cap B=\emptyset\)。

证明

以下所有仅关于 \(a\) 的定理与 \(b\) 是对称的。

• 引理一：\(\lfloor n\times a\rfloor+1\le \lfloor (n+1)\times a\rfloor(n\in \mathbb{N})\)。
  证明：因为 \(a,b>0,\frac{1}{a}<1,\frac{1}{b}<1\)，所以 \(a,b>1\)，给非负数增加一个 \(>1\) 的数肯定会导致整数部分至少 \(+1\)。
  • 推论：\(\lfloor n\times a\rfloor\) 互不相同。
  • 推论：\(\lfloor (n+1)\times a\rfloor\ge 1\)。
    • 推论：\(A\cup B\subseteq\mathbb{N}^{+}\)
• 引理二：不存在 \(x\in A,x\in B\)。
  证明：因为 \(A\cup B\subseteq\mathbb{N}^+\)，所以 \(x\in\mathbb{N}^+\)，设 \(x=\lfloor n\times a\rfloor=\lfloor m\times b\rfloor(n,m\in \mathbb{N}^{+})\)，因为 \(a,b\) 是无理数所以取不到等号，\(x<n\times a<x+1\)。
  \[x<n\times a<x+1\\[0.2cm] \frac{x}{n}<a<\frac{x+1}{n}\\[0.2cm] \frac{n}{x+1}<\frac{1}{a}<\frac{n}{x}\]
  同理我们有 \(\frac{m}{x+1}<\frac{1}{b}<\frac{m}{x}\)。两式相加得：
  \[\frac{n+m}{x+1}<\frac{1}{a}+\frac{1}{b}<\frac{n+m}{x}\\[0.2cm] \frac{n+m}{x+1}<1<\frac{n+m}{x}\\[0.2cm] \frac{x}{n+m}<1<\frac{x+1}{n+m}\\[0.2cm] x<n+m<x+1\]
  显然这与 \(n,m,x\in\mathbb{N}^+\) 冲突。
  • 推论：\(A\cap B=\emptyset\)。
• 引理三：不存在 \(x\notin A,x\notin B,x\in\mathbb{N}^+\)。
  证明：设 \(\lfloor n\times a\rfloor<x<\lfloor (n+1)\times a\rfloor\)，然后我们把式子拆开分析：
  \[\lfloor n\times a\rfloor<x\\[0.2cm] n\times a<x\\[0.2cm] a<\frac{x}{n}\\[0.2cm] \frac{n}{x}<\frac{1}{a}\\[0.2cm]\]
  手动间隔。
  \[x<\lfloor (n+1)\times a\rfloor\\[0.2cm] x\le\lfloor (n+1)\times a-1\rfloor\\[0.2cm] x+1<(n+1)\times a\\[0.2cm] \frac{x+1}{n+1}<a\\[0.2cm] \frac{x+1}{n+1}<a\\[0.2cm] \frac{1}{a}<\frac{n+1}{x+1} \]
  合并两式得 \(\frac{n}{x}<\frac{1}{a}<\frac{n+1}{x+1}\)，同理有 \(\frac{m}{x}<\frac{1}{b}<\frac{m+1}{x+1}\)，两式相加得 \(\frac{n+m}{x}<1<\frac{n+m+2}{x+1}\)，把式子拆开分析：
  \[\frac{n+m}{x}<1\\[0.2cm] n+m<x\\[0.2cm] 1<\frac{n+m+2}{x+1}\\[0.2cm] x+1<n+m+2 \]
  合并两式得 \(n+m<x<x+1<n+m+2\)，显然这与 \(n,m,x\in\mathbb{N}\) 冲突。
  • 推论：\(A\cup B\supseteq\mathbb{N}^{+}\)

---

我们假设有 \(a,b\) 满足前文我们发现的对于任一项 \(i\) 都有用的公式：\(\lfloor a\times n\rfloor+n=\lfloor b\times n\rfloor\)

来解方程：

\[\begin{cases} \lfloor a\times n\rfloor+n=\lfloor b\times n\rfloor\\ \frac{1}{a}+\frac{1}{b}=1\\ a>0\\ b>0 \end{cases} \]

• 一式：
  \[\lfloor a\times n\rfloor+n=\lfloor b\times n\rfloor\\[0.2cm] \lfloor a\times n+n\rfloor=\lfloor b\times n\rfloor\\[0.2cm] \lfloor (a+1)\times n\rfloor=\lfloor b\times n\rfloor \]
  如果 \(a+1\not=b\)，那么一定存在一个 \(n\) 使得 \(\lfloor (a+1)\times n\rfloor=\lfloor b\times n\rfloor\)，差不多就是考虑 \(n=O(|a+1-b|)\) 的时候。所以 \(b=a+1\)。
  合并两式得

\[\begin{cases} b=a+1\\ \frac{1}{a}+\frac{1}{b}=1\\ a>0\\ b>0 \end{cases} \]

\[\frac{1}{a}+\frac{1}{a+1}=1\\[0.2cm] \frac{a+1}{a^2+a}+\frac{a}{a^2+a}=1\\[0.2cm] \frac{2\times a+1}{a^2+a}=1\\[0.2cm] 2\times a+1=a^2+a\\[0.2cm] -a^2+a+1=0\\ a=-\frac{-1\plusmn\sqrt{5}}{2} \]

取正根 \(\frac{1+\sqrt{5}}{2}=\varphi\)，则我们的通项公式为 \(a_i=\lfloor\varphi\times i\rfloor,b_i=a_i+i\)。

这篇博客写了两个小时。