bzoj1010 [HNOI2008]玩具装箱toy
1010: [HNOI2008]玩具装箱toy
Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 12173 Solved: 5227
[Submit][Status][Discuss]
Description
P教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压
缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。P教授有编号为1...N的N件玩具,第i件玩具经过
压缩后变成一维长度为Ci.为了方便整理,P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容
器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物,形式地说如果将第i件玩具到第j个玩具放到一
个容器中,那么容器的长度将为 x=j-i+Sigma(Ck) i<=K<=j 制作容器的费用与容器的长度有关,根据教授研究,
如果容器长度为x,其制作费用为(X-L)^2.其中L是一个常量。P教授不关心容器的数目,他可以制作出任意长度的容
器,甚至超过L。但他希望费用最小.
Input
第一行输入两个整数N,L.接下来N行输入Ci.1<=N<=50000,1<=L,Ci<=10^7
Output
输出最小费用
Sample Input
5 4
3
4
2
1
4
3
4
2
1
4
Sample Output
1
分析:这道题利用决策单调性和斜率优化都能做.说一下决策单调性.
很容易写出状态转移方程:![]() ,仔细瞅瞅,这不是一个经典模型吗?
,仔细瞅瞅,这不是一个经典模型吗?![]() ,只是i变成了i+1.
,只是i变成了i+1.
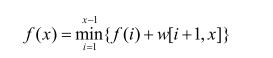 ,仔细瞅瞅,这不是一个经典模型吗?
,仔细瞅瞅,这不是一个经典模型吗?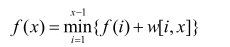 ,只是i变成了i+1.
,只是i变成了i+1. 这个模型有什么特殊的地方呢?如果它满足![]() ,那么就可以利用决策单调性优化成O(nlogn)的复杂度了. 怎么证明本题是否满足呢?作差法强行化简,这个式子是成立的.
,那么就可以利用决策单调性优化成O(nlogn)的复杂度了. 怎么证明本题是否满足呢?作差法强行化简,这个式子是成立的.
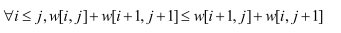 ,那么就可以利用决策单调性优化成O(nlogn)的复杂度了. 怎么证明本题是否满足呢?作差法强行化简,这个式子是成立的.
,那么就可以利用决策单调性优化成O(nlogn)的复杂度了. 怎么证明本题是否满足呢?作差法强行化简,这个式子是成立的. 如果是这样的,对于每一个位置标一个数字,表示它是从哪一个地方转移而来的,可能长这样:![]() ,或者这样:
,或者这样:![]() ,但绝对不会这样:
,但绝对不会这样:![]() 也就是说它是一段段连续的区间,并且数字是递增的.
也就是说它是一段段连续的区间,并且数字是递增的.
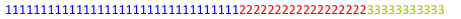 ,或者这样:
,或者这样: ,但绝对不会这样:
,但绝对不会这样: 也就是说它是一段段连续的区间,并且数字是递增的.
也就是说它是一段段连续的区间,并且数字是递增的. 那么我们的做法就很明显了:维护一个栈,每次加进来一个点时,更新它后面的点决策的位置.
怎么更新?假设我们新加进来的点是3,对应第一个图,如果在老决策2的起点处决策没有3优,那么就把2的区间给并到3的区间上,如图2.否则就二分这个分界点,变成图1的样子.
每个点只会出栈一次,均摊时间O(1),有二分查找,复杂度O(logn),总体复杂度O(nlogn).
代码写起来还是有点麻烦的.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const int maxn = 60010; struct node { int l,r,p; } e[maxn]; ll n,L,c[maxn],sum[maxn],f[maxn],tot; ll cal(ll x,ll y) { ll temp = y - x - 1 + sum[y] - sum[x] - L; return temp * temp; } ll get(ll x,ll y) { return f[x] + cal(x,y); } ll find(node temp,ll pos) { ll l = temp.l,r = temp.r,ans = temp.r + 1; while (l <= r) { ll mid = (l + r) >> 1; if (get(pos,mid) < get(temp.p,mid)) { ans = mid; r = mid - 1; } else l = mid + 1; } return ans; } void solve() { f[1] = (c[1] - L) * (c[1] - L); node temp; temp.l = 1; temp.r = n; temp.p = 0; e[++tot] = temp; int cur = 1; for (int i = 1; i <= n; i++) { if (e[cur].r < i) cur++; f[i] = get(e[cur].p,i); while (1) { node temp = e[tot]; if (get(i,temp.r) < get(temp.p,temp.r)) { if (get(i,temp.l) < get(temp.p,temp.l)) { tot--; continue; } else { int x = find(temp,i); e[tot].r = x - 1; break; } } else break; } if(e[tot].r < n) { node temp; temp.l = e[tot].r + 1; temp.r = n; temp.p = i; e[++tot] = temp; } } } int main() { scanf("%lld%lld",&n,&L); for (int i = 1; i <= n; i++) scanf("%lld",&c[i]); for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + c[i]; solve(); printf("%lld\n",f[n]); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号