bzoj3994 [SDOI2015]约数个数和
3994: [SDOI2015]约数个数和
Time Limit: 20 Sec Memory Limit: 128 MBSubmit: 1125 Solved: 780
[Submit][Status][Discuss]
Description
设d(x)为x的约数个数,给定N、M,求 ![]()

Input
输入文件包含多组测试数据。
第一行,一个整数T,表示测试数据的组数。
接下来的T行,每行两个整数N、M。
Output
T行,每行一个整数,表示你所求的答案。
Sample Input
2
7 4
5 6
7 4
5 6
Sample Output
110
121
121
HINT
1<=N, M<=50000
1<=T<=50000
Source
分析:详见:传送门
提一点: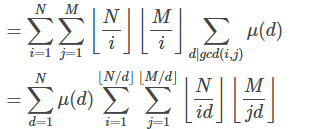 为什么从上面那个式子变到下面i 就变成了 id,j就变成了jd呢?
为什么从上面那个式子变到下面i 就变成了 id,j就变成了jd呢?
因为第一个式子枚举的d是gcd(i,j)的因数,那么i和j必然是d的倍数.为了保证答案的合法性,必须要变成这样.
记住一点: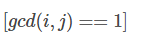 等价于
等价于 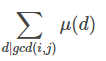 .
.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; ll prime[50010], vis[50010], tot, sum[50010], mo[50010], f[50010], T, n, m; void init() { mo[1] = 1; for (ll i = 2; i <= 50000; i++) { if (!vis[i]) { prime[++tot] = i; mo[i] = -1; } for (ll j = 1; j <= tot; j++) { ll t = prime[j] * i; if (t > 50000) break; vis[t] = 1; if (i % prime[j] == 0) { mo[t] = 0; break; } mo[t] = -mo[i]; } } for (ll i = 1; i <= 50000; i++) sum[i] = sum[i - 1] + mo[i]; } void gen(ll x) { ll res = 0, last = 0; for (ll i = 1; i <= x; i = last + 1) { last = x / (x / i); res += (last - i + 1) * (x / i); } f[x] = res; } ll solve() { ll res = 0, last = 0; for (ll i = 1; i <= min(n, m); i = last + 1) { last = min(n / (n / i), m / (m / i)); res += (sum[last] - sum[i - 1]) * f[n / i] * f[m / i]; } return res; } int main() { init(); for (ll i = 1; i <= 50000; i++) gen(i); scanf("%lld", &T); while (T--) { scanf("%lld%lld", &n, &m); printf("%lld\n", solve()); } return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号