Python基础篇---装饰器补充，递归函数和初始算法

本章内容 

      • 装饰器补充

      • 递归函数

      • 算法之二分法

装饰器补充

---

多层装饰器

上一章我们学习了装饰器和装饰器语法糖，当我们有多个装饰器的时候，我们可以在一个函数上叠加多个装饰器。

def outter1(func1):
    print('加载了outter1')
    def wrapper1(*args, **kwargs):
        print('执行了wrapper1')
        res1 = func1(*args, **kwargs)
        return res1
    return wrapper1

def outter2(func2):
    print('加载了outter2')
    def wrapper2(*args, **kwargs):
        print('执行了wrapper2')
        res2 = func2(*args, **kwargs)
        return res2
    return wrapper2

def outter3(func3):
    print('加载了outter3')
    def wrapper3(*args, **kwargs):
        print('执行了wrapper3')
        res3 = func3(*args, **kwargs)
        return res3
    return wrapper3

使用方法和原理

@outter1  # index = outter1(wrapper2)
@outter2  # wrapper2 = outter2（wrapper3）
@outter3  # wrapper3 = outter3(index)
def index():
    print('from index')
# @outter3紧贴index()，所以此时outter3调用的是index()，而返回的实际上是wrapper3，所以wrapper3 = outter3（index）
# @outter3的调用完之后，这时@outter2看到的是wrapper3，所以这时outter2调用的就是wrapper3,而返回的是wrapper2，所以有 wrapper2 = outter2(wrapper3)
# 同理，当@outter2调用完之后，@outter1看到的就是wrapper2，所以outter1这时调用的就是wrapper2，因为outter1的上层没有语法糖继续调用，所以这里就给它起名和被装饰函数同名，也就是index，所以有index = outter1(wrapper2)

有参装饰器

有参装饰器是为装饰器提供多样功能选择的实现提供的，实现原理是三层闭包。

有参装饰器的模板

def outter(x):  # 再利用一层函数对装饰器进行闭 传入形参
    def  login_auth(func):
        def wrapper(*args,*kwargs):
            res = func(*args,**kwargs)
            print(x)   # 利用包的原理去调用最外层传入的实参
            return res 
        return wrapper
      return login_auth

通过第三层进行传值，使得有参装饰器可以使用其他参数，实现其他功能。

有参装饰器的语法糖

@outer('3')
def index():
    print('from index')

# @outer('3')
# 1.左侧是语法糖结构 右侧是函数名加括号结构   
# 2.先执行函数调用  outer('3')  返回值是login_auth
# 3.在执行语法糖结构  @login_auth

'''
函数名加括号 执行优先级最高
'''

 

递归函数

---

在编程语言中，如果一个函数在运行过程中直接或间接的调用了自身，我们称这个函数为递归函数。

递归函数的特性：

           1.必须要有明确的结束条件，不是无限循环的过程。

           2. 每次递归 复杂度必须降低(下一次递归要比上一次递归解答)，越往下递归应该离解决问题的答案越近

例子：

"""
需求:我想知道我们班坐在第一排的某个学生年龄
过程:
    我问他多大了 他调皮不告诉我 说比后面那个同学大两岁
    后面的说比他后面的大两岁
    ...
    问到最后你一排 终于开口说 18岁
    ...
    知道最后一排的年级回推就可以知道第一排的年级
名词:
    递推:一层层往下问
    回溯:根据结果推结论
"""
# 如何编写代码完成
    # 目标人物的年龄 = 后一排年龄 + 2
    # 后一排年龄 = 后后一排年龄 + 2
    # 后后一排年龄 = 后后后一排年龄 + 2
    # 后后后后一排年龄 = 18
# 将求问年龄变成函数
    # age(5) = age(4) + 2
    # age(4) = age(3) + 2
    # age(3) = age(2) + 2
    # age(2) = age(1) + 2
    # age(1) = 18

# 封装函数
def get_age(n):
    if n == 1:
        return 18  # 有明确的结束条件
    return get_age(n-1) + 2
print(get_age(4))

如果递归函数没有结束的条件，则会报错，提示这个项目超出最大递归深度。

# import sys
# print(sys.getrecursionlimit())  # 获取默认的最大递归深度  # 1000
# sys.setrecursionlimit(2000)  # 还可以修改最大递归深度

递归的练习

l1 = [1,[2,[3,[4,[5,[6,[7,[8,[9,]]]]]]]]]
'''需求:循环打印出列表中每一个数字'''
# 写代码之前一定要先理清思路
"""
完整步骤 
    1.for循环大列表
    2.判断元素是否是数字 如果是则打印
    3.如果不是则for循环
    4.判断元素是否是数字 如果是则打印
    5.如果不是则for循环
    6.判断元素是否是数字 如果是则打印
    7.如果不是则for循环
ps:重复做一些事情 但是每次都比上一次简单一些 >>>:  递归函数
"""
def get_num(l):
    for i in l:  # 自带结束条件 并且每次传入的数据都比上一次简单
        if isinstance(i,int):  # 判断某个数据是否属于某个类型
            print(i)
        else:
            get_num(i)
get_num(l1)

算法之二分法

---

算法是什么？算法就是解决问题的有效方法，而二分算法就是入门的算法。

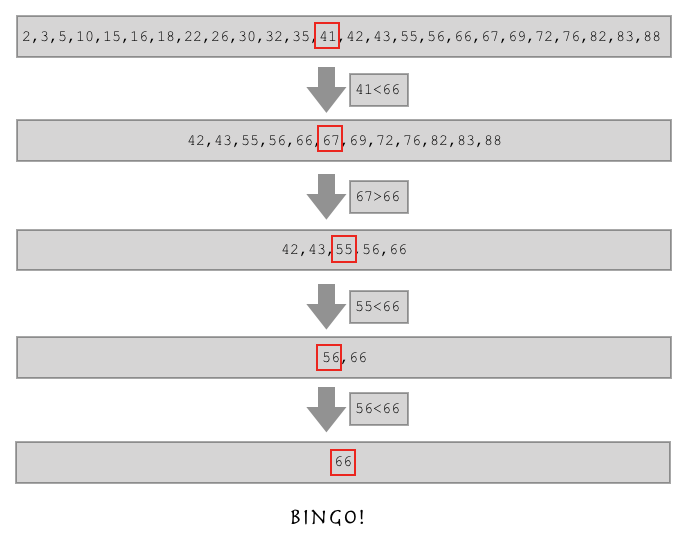
如果有这样一个列表，让你从这个列表中找到66的位置，你要怎么做？

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

# 方法1
l.index(66)

# 方法2
i = 0
for num in l:
    if num == 66:
        print(i)
    i+=1

上面的方法确实可以帮助我们找到66所在的位置，但我们不用index或者说列表的长度是几十万个，一个一个对比的话是不是很慢，效率太低了，所以我们像了个办法。

二分法

我们使用二分法的前提：数据集必须是有顺序的(升序或者降序)。

当前我们需要找的列表是不是就是一个升序的列表，我们可以用二分法去找66的位置。

如果这样，假如我要找的数比列表中间的数还大，是不是我直接在列表的后半边找就行了？按照这个思路去找。

代码的实现

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

def func(l,aim):
    mid = (len(l)-1)//2
    if l:
        # 2.判断中间索引对应的数据与目标数据的大小
        if aim > l[mid]: # 保留右侧的数据集
            func(l[mid+1:],aim)  # 对右侧继续二分 重复执行相同代码 并且复杂度降低
        elif aim < l[mid]:   # 保留左侧的数据集
            func(l[:mid],aim)  # 对左侧继续二分 重复执行相同代码 并且复杂度降低
        elif aim == l[mid]:  # 刚好是中间的值
            print("bingo",aim)  # 输出值
    else:
        print('找不到',aim)
func(l,66)
func(l,6)

二分法的缺陷：

       1.如果要找的元素就在数据集的开头，二分更加复杂了。

       2.数据集必须有顺序限制。