学习札礼——搜索与图论

树与图的存储
树是一种特殊的图，与图的存储方式相同。 树是无环连通图

对于无向图中的边ab，存储两条有向边a->b, b->a。

因此我们可以只考虑有向图的存储。

(1) 邻接矩阵：g[a][b] 存储边a->b

(2) 邻接表：

// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;

// 添加一条边a->b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);

　　

深度优先搜索：DFS（Depth-First-Search）

宽度优先搜索：BFS（Breadth-First-Search）

DFS和BFS的对比

DFS使用栈（stack）来实现，BFS使用队列（queue）来实现

DFS所需要的空间是树的高度h，而BFS需要的空间是2^h 

BFS具有最短路的特性，DFS不具有最短路的特性

时间复杂度 O(n+m)O(n+m), nn 表示点数，mm 表示边数

(1) 深度优先遍历

DFS中的2个重要概念：

回溯：回溯的时候，一定要记得恢复现场
剪枝：提前判断某个分支一定不合法，直接剪掉该分支

 

 

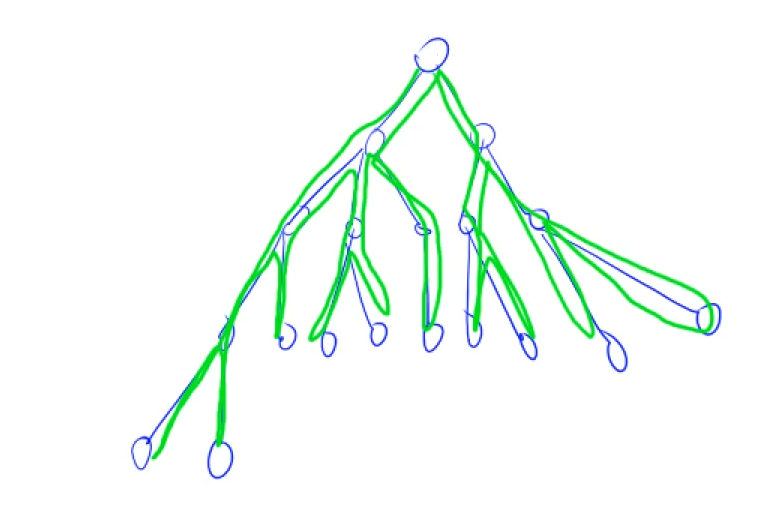
int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

　　

(2) 宽度优先遍历

 

 

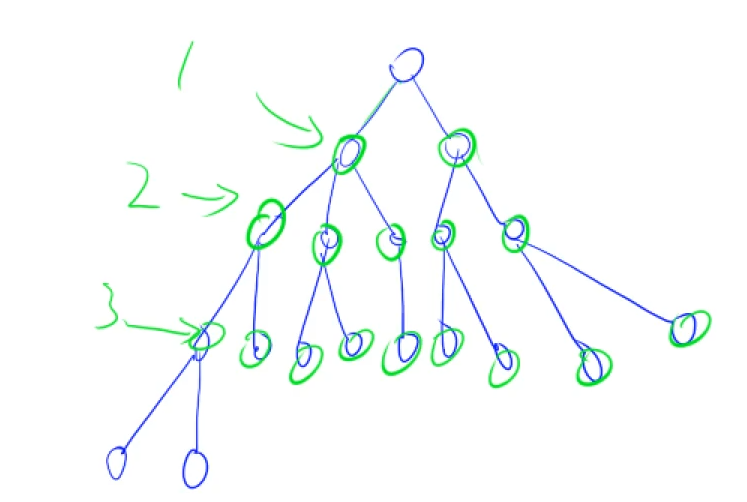
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}