数列的极限（三）

重要定理

 

 

 

 

数列极限的四则运算

若lim（an，n,inf)=a,lim（bn，n,inf)=b（意思是都有极限）

则有lim（an+bn，n,inf)=lim（an，n,inf)+lim（bn，n,inf) =a+b(减法和乘法也适应）

特别地，若C为常数lim（an+C，n,inf)=lim（an，n,inf)+lim（C，n,inf) =C*lim（an，n,inf) （因为常数极限等于常数本身）

对于除法：lim（an/bn，n,inf)=lim（an，n,inf)/lim（bn，n,inf) =a/b (要求B！=0）

但极限的四则运算不能推广到无限项：

比如lim（1/n+1/n+...+1/n(有n项），n，inf）=lim（1，n，inf)=1

小技巧：若证明两个数列存在极限，可以先不证明两个数列的极限存在，而是直接证明四则运算的数列存在极限，也就证明了原数列都存在极限（不一定能成功，因为可能其中之一没有极限）

 

重要公式：

 

 

 

lim(n^k/(n^m),n,inf)为原式

 

 

 

 示例：

例一

lim（(n^2-100n+4*n^0)/(3n^2-90*n +5*n^0),n,inf)

因为分子是形如n^k的指数函数，最高次幂为2，分母是形如n^m的指数函数,也为2.

所以只需要比较分子分母有最高次幂项的斜率，n^2的斜率为1，3n^2的斜率为2，又依据公式最高次幂相同时，函数极限为分子分母有最高次幂项的斜率的比值，所以，本题极限为：

1/3;

例二

lim（(3n^(4/3)-n-1)/(4n^4-3*n^3 +n+1),n,inf)的极限为0.因为4>4/3 (也就是m>k的情况下，极限为0）

例三

 

 

例四

 

 

例五

 

两个重要定理

夹逼定理

若存在N0，当n>N0时有

an<cn<bn

且

lim（an,n,inf)=a

lim（bn,n,inf)=a ;

则数列{cn}收敛且

lim（cn,n,inf)=a

 

 

 注：若一个数列有很多项相加或相乘，但是不能化简，不能用极限的四则运算时，可以尝试用夹逼定理。

例题

例一

 lim（（a^n+b^n+c^n)(1/n),n,inf) (a>=b>=c>0,常数）

 

 例二

 

 

 

 

 

单调有界定理

若数列{an}单调递增有上界（a1<=a2<=a3....<=an<=...递增，存在常数M，对所有的n>N，都有an<=M,，称之为有上界；依据递增数列定义下界是a1）

则

{an}收敛。

反之若单调递减数列有下界，也是收敛的。

即{an}单调且有界，则{an}收敛。

注：定理条件可以减弱为：{an}，当n>N0时，单调有界，则{an}收敛。

注二：若{an}是由递推关系式给出，或证明{an}收敛，并求极限，或者证明{an}收敛，或者不能用夹逼定理，尝试用单调有界定理。

 

特殊数列{（1+（1/n)^n) }的收敛性

 

 

 

 

 因为算术平均数大于几何平均数，所以上图最下面一项成立

 

 

 

 所以原数列有上界，则原数列有极限

 

 

 

 

 极限为e，要求记下来，非常重要

 

 

 重要不等式

 

 

例题 

 

 

 

 

 

 

 

 

 

 

 

 

 一元二次方程求根公式

 

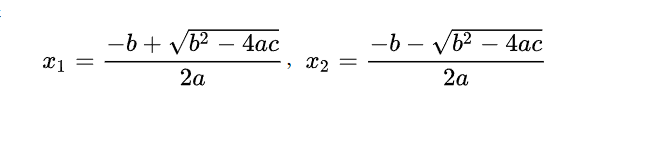
 因为函数开口向上，所以当xn小于0点时，原函数小于0

 

 

 

 

 

 

 

单调有界定理及应用

例一

 

 

 

 

 例二

 

 

子数列与子数列推论

某数列有极限当且仅当其全部子数列有极限且极限相等

 因为nk是原数列的下标，k是子列中对应的项的下标。原数列的第2项，可能是子列的第1项，即nk=2时，k可能等于1. 但原数列的第1项不可能是子列的第2项，即nk=1时, k不可能等于2. 以此类推，所以nk>=k.

 

 

 

 

子数列推论