A 第二课栈_队列_堆

内容概览及预备知识：

预备知识：栈与队列：

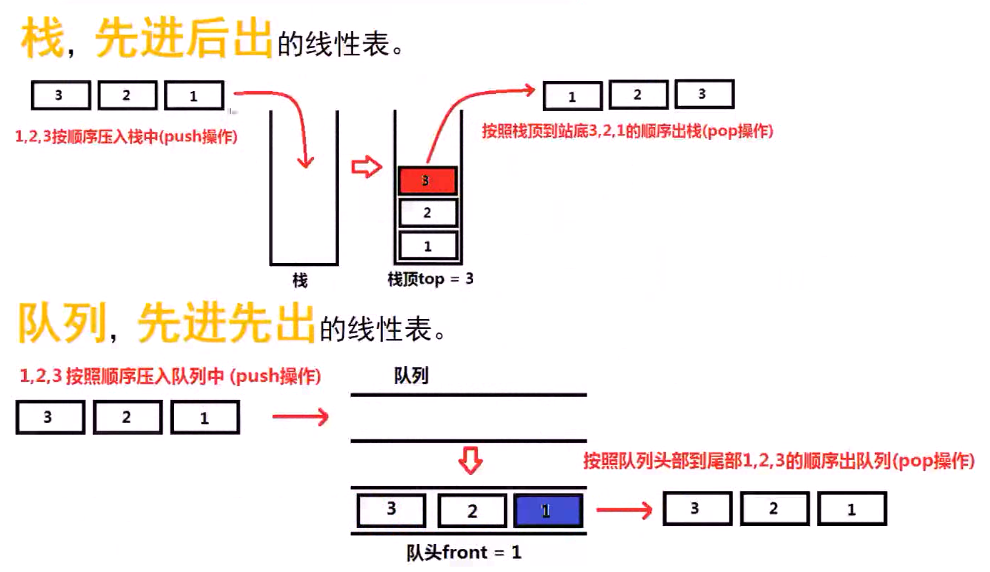
STL基本的栈操作(stack)：

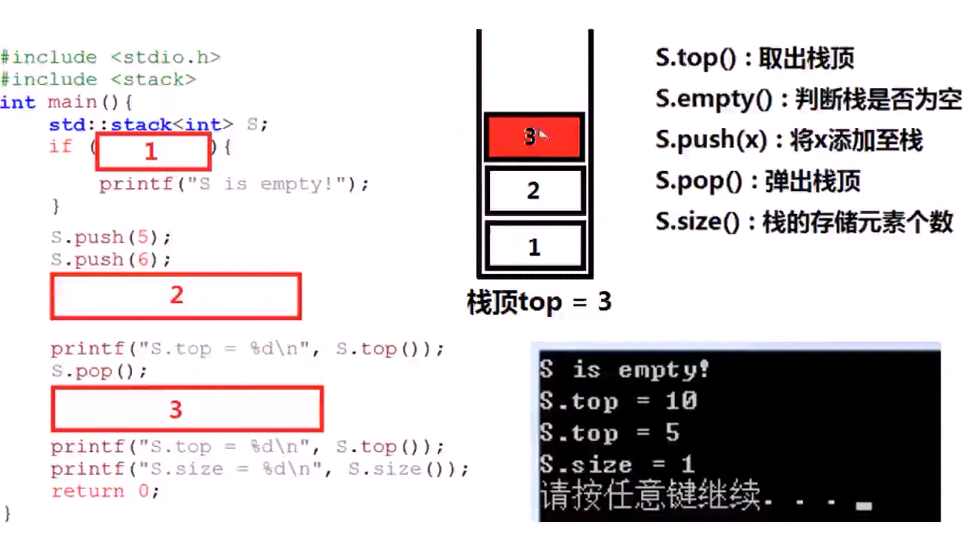
 1 #include <iostream>
 2 using namespace std;
 3 
 4 #include <stack>
 5 int main(){
 6     stack <int> stk;
 7     if(stk.empty()){ //判断是否为空 isempty()
 8         cout <<"The Stack is empty!!!"<<endl;
 9     }
10     stk.push(5); //压栈
11     stk.push(6);
12     stk.push(10);
13 
14     cout <<"The Stack' top is " <<stk.top()<<endl;
15     stk.pop(); //弹出栈顶
16     stk.pop();
17     cout <<"The Stack' top is "<<stk.top()<<endl;
18     cout <<"The Stack' size is "<<stk.size()<<endl; //栈中的size
19 
20     return 0;
21 }

View Code

STL基本的队列操作（queue）：

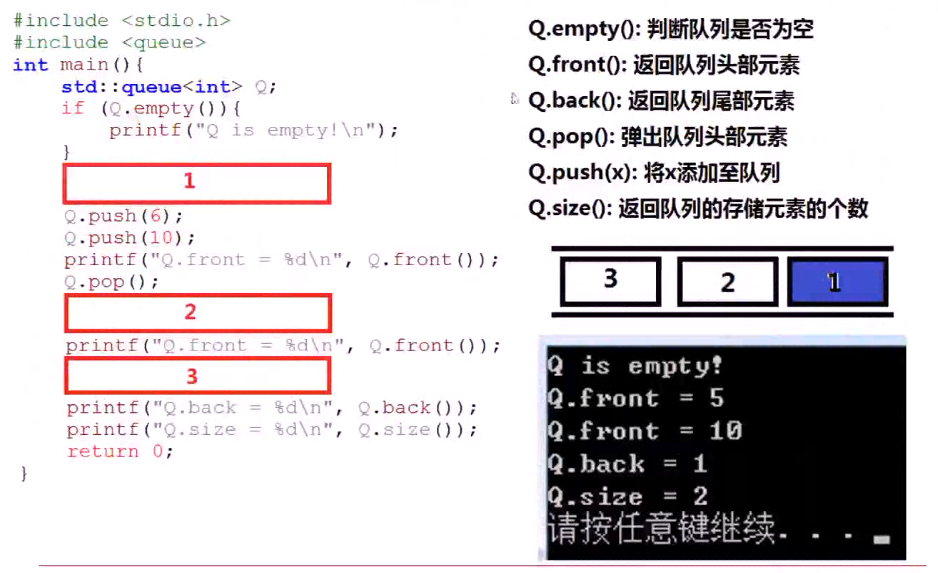
 1 #include <iostream>
 2 using namespace std;
 3 
 4 #include <queue>
 5 int main(){
 6     queue <int> quu;
 7     if(quu.empty()){
 8         cout << "The Queue is empty!"<<endl;
 9     }
10     quu.push(5); //加入队列
11     quu.push(6);
12     quu.push(10);
13 
14     cout<<"The Queue' front is "<<quu.front()<<endl;
15     quu.pop(); //从队列头拿出
16     quu.pop();
17     cout<<"The Queue' front is "<<quu.front()<<endl;//队头
18     quu.push(1);  //队列后加入 1
19     cout<<"The Queue' back is "<<quu.back()<<endl; //队尾
20 
21 
22     cout<<"The Queue' size is "<<quu.size()<<endl; //队列的大小
23 
24     return 0;
25 }

View Code

例1：使用队列实现栈（No.225）：

思路及代码：

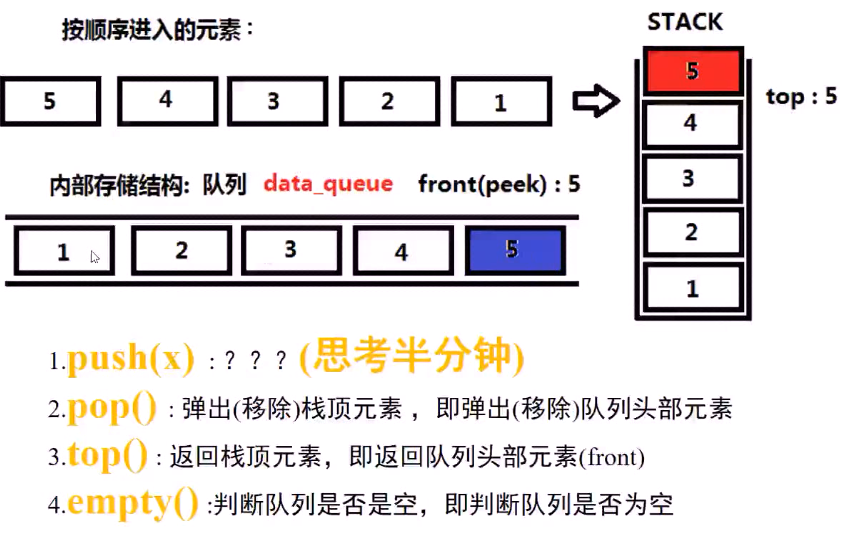
假设前4个已经调整好了，下面是如何调整第五个！！！

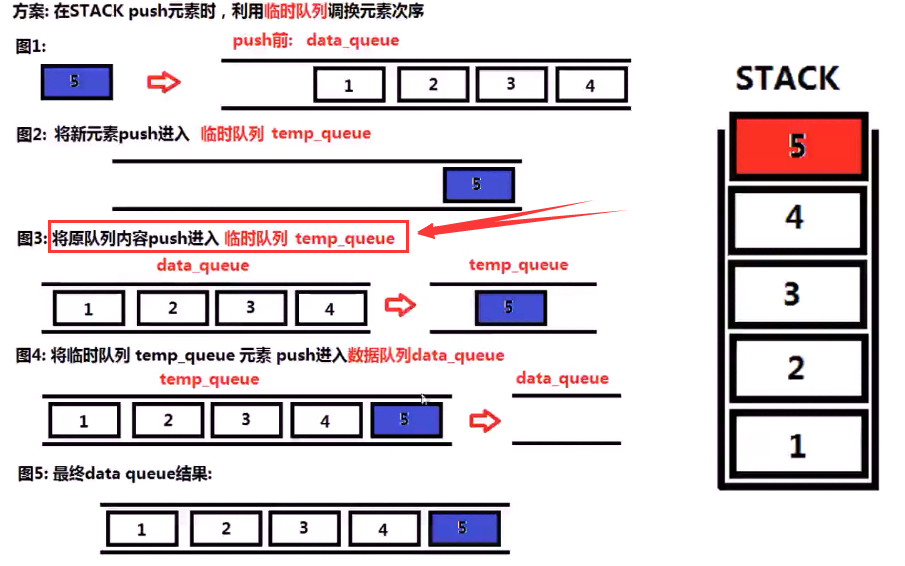
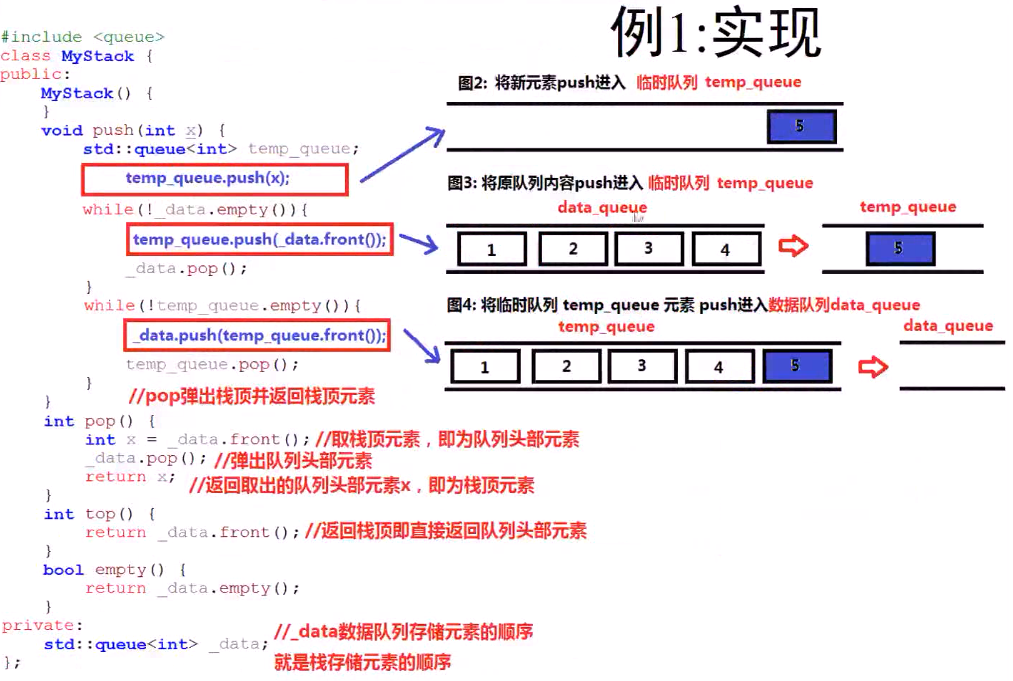
代码：

 1 class MyStack{
 2 public:
 3     MyStack(){}
 4     void push(int x){
 5         queue <int> temp_queue; //临时队列
 6         temp_queue.push(x);
 7         while(!_data.empty()){ //将_data中的数据push 到临时队列
 8             temp_queue.push(_data.front());
 9             _data.pop();
10         }
11         while(!temp_queue.empty()){ //将 temp_queue中重新放入到_data中
12              _data.push(temp_queue.front());
13              temp_queue.pop();
14         }
15     }
16 
17     int pop(){
18         int x = _data.front();
19         _data.pop();
20         return x;
21     }
22 
23     int top(){
24         return _data.front();
25     }
26 
27     bool empty(){
28         return _data.empty();
29     }
30 private:
31     queue <int> _data; // _data中存储的是 栈存储的顺序
32 };

View Code

 1 #include <iostream>
 2 using namespace std;
 3 
 4 #include <queue>
 5 
 6 class MyStack{
 7 public:
 8     MyStack(){}
 9     void push(int x){
10         queue <int> temp_queue; //临时队列
11         temp_queue.push(x);
12         while(!_data.empty()){ //将_data中的数据push 到临时队列
13             temp_queue.push(_data.front());
14             _data.pop();
15         }
16         while(!temp_queue.empty()){ //将 temp_queue中重新放入到_data中
17              _data.push(temp_queue.front());
18              temp_queue.pop();
19         }
20     }
21 
22     int pop(){
23         int x = _data.front();
24         _data.pop();
25         return x;
26     }
27 
28     int top(){
29         return _data.front();
30     }
31 
32     bool empty(){
33         return _data.empty();
34     }
35 private:
36     queue <int> _data; // _data中存储的是 栈存储的顺序
37 };
38 
39 
40 
41 int main(){
42     MyStack * stk = new MyStack();
43     stk->push(2);
44     stk->push(4);
45     stk->push(8);
46     int a = stk->pop();
47     int b = stk->top();
48     bool c = stk->empty();
49     cout <<a <<b<<c<<endl;
50 
51     return 0;
52 }

view code

例2：使用栈实现队列（No.232）：

思路及代码：

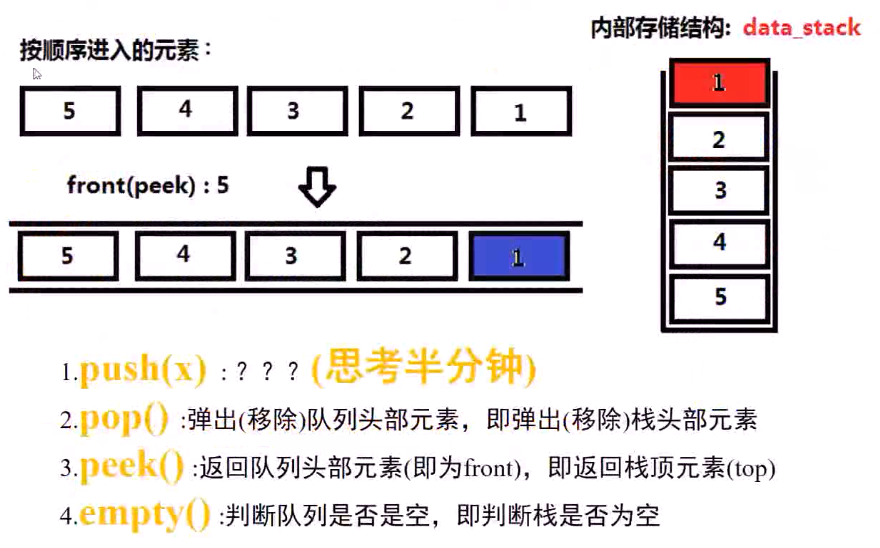
和例1一样，先假设已经有了四个元素，现在准备插入第五个元素，就是如何将5 放到栈的最下面！！！

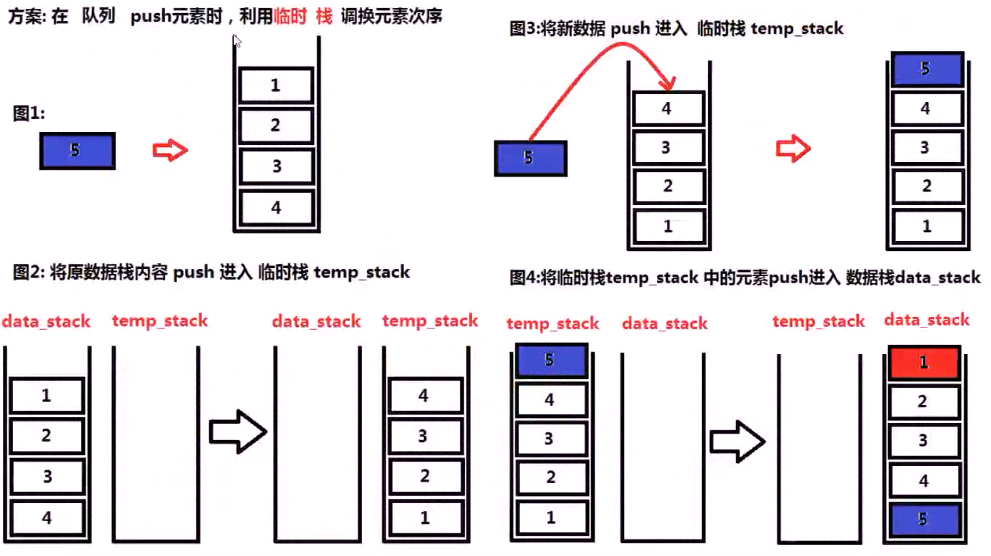
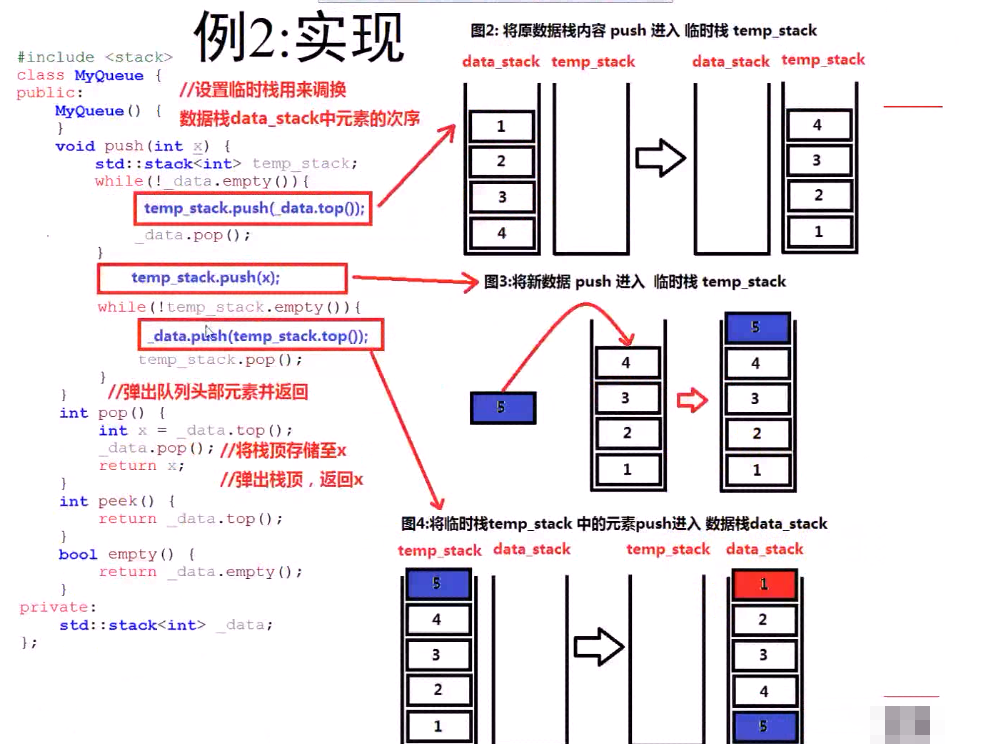
 1 class MyQueue{
 2 public:
 3     MyQueue(){}
 4     void push(int x) {
 5         //先将原有的栈中元素都出栈  进入临时栈中 temp_stk 
 6         stack <int> temp_stk;
 7         while(!_data_stk.empty()){
 8             temp_stk.push(_data_stk.top());
 9             _data_stk.pop();  
10         }
11         _data_stk.push(x);  //将要加入的放到临时栈中
12         while(!temp_stk.empty()){  //最后再将临时中的元素全部转回到data_stack中
13             _data_stk.push(temp_stk.top());
14             temp_stk.pop();  
15         }
16     }
17     
18     int pop(){
19         int x = _data_stk.top();
20         _data_stk.pop(); //返回类型是void 
21         return x;
22     }
23     int peek(){ //front
24         return _data_stk.top();
25     }
26     bool empty(){
27         return _data_stk.empty();
28     }
29 
30 private:
31     stack <int> _data_stk;
32 };

LeetCode 代码

 1 #include <iostream>
 2 using namespace std;
 3 
 4 #include <stack>
 5 
 6 class MyQueue{
 7 public:
 8     MyQueue(){}
 9     void push(int x) {
10         //先将原有的栈中元素都出栈  进入临时栈中 temp_stk
11         stack <int> temp_stk;
12         while(!_data_stk.empty()){
13             temp_stk.push(_data_stk.top());
14             _data_stk.pop();
15         }
16         _data_stk.push(x);  //将要加入的放到临时栈中
17         while(!temp_stk.empty()){  //最后再将临时中的元素全部转回到data_stack中
18             _data_stk.push(temp_stk.top());
19             temp_stk.pop();
20         }
21     }
22 
23     int pop(){
24         int x = _data_stk.top();
25         _data_stk.pop(); //返回类型是void
26         return x;
27     }
28     int front(){ //peek()  
29         return _data_stk.top();
30     }
31     bool empty(){
32         return _data_stk.empty();
33     }
34 
35 private:
36     stack <int> _data_stk;
37 };
38 
39 
40 int main(){
41 
42     return 0;
43 }

本地

注：例1 和例2 的时间复杂度都是O(n) 的。

例3：包含min函数的栈（No.155）：

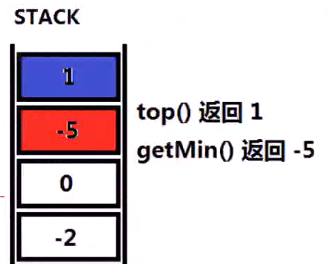
注：这里要求时间复杂度为 O(1)

思路及代码：

因为时间复杂度是O(1),所以肯定不能通过遍历等完成，

思考：要用1个变量记录最小值？

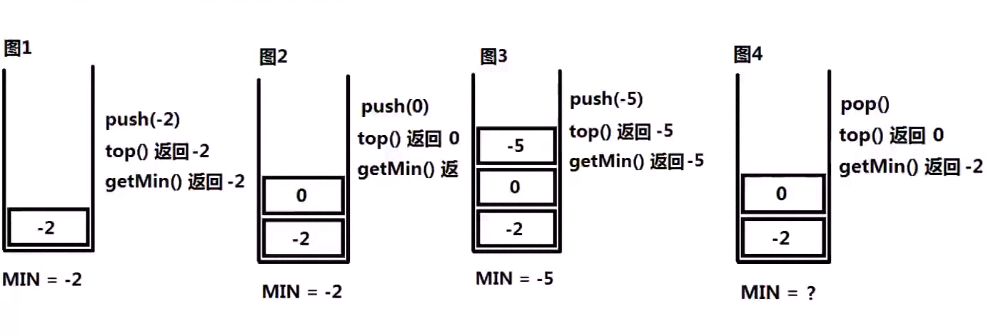
所下：

最终的思路如下：

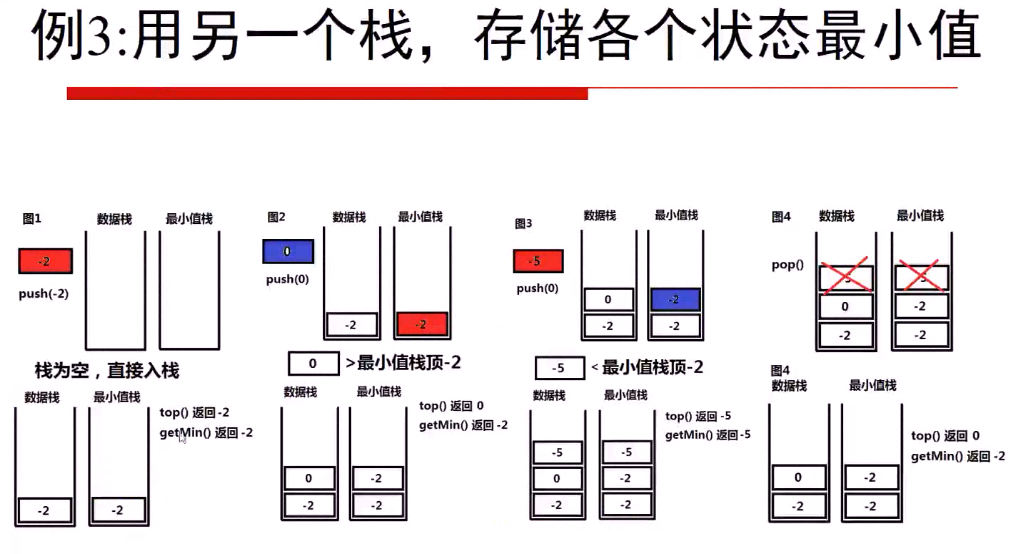
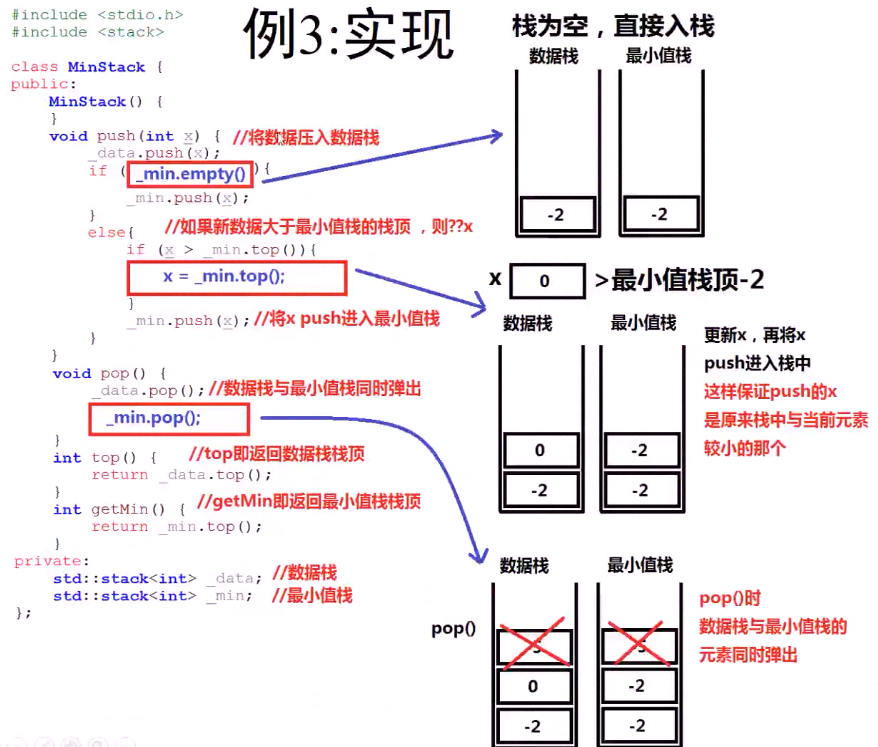
 1 class MinStack{
 2 public:
 3     //构造函数
 4     MinStack(){}
 5     //将元素x压入栈中
 6     void push(int x){
 7         stk_data.push(x);
 8         if(stk_min.size()==0){
 9             stk_min.push(x);
10         }else if(x >= stk_min.top()){
11             stk_min.push(stk_min.top());
12         }else{
13             stk_min.push(x);
14         }
15     }
16     //将栈顶元素弹出
17     void pop(){
18         stk_data.pop();
19         stk_min.pop();
20     }
21     //返回栈顶元素
22     int top(){
23         return stk_data.top();
24     }
25     //返回栈内的最小元素
26     int getMin(){
27         return stk_min.top();
28     }
29 private:
30     stack <int> stk_data;
31     stack <int> stk_min;
32 };

LeetCode 代码

例4：合法的出栈序列（poj.1363）：

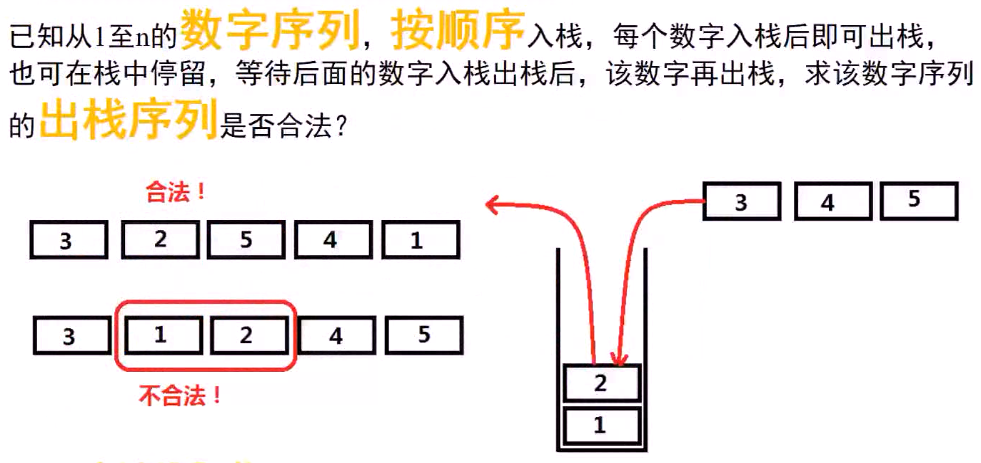
原题介绍和 POJ介绍：

思路及代码：

思考：模拟入栈过程：

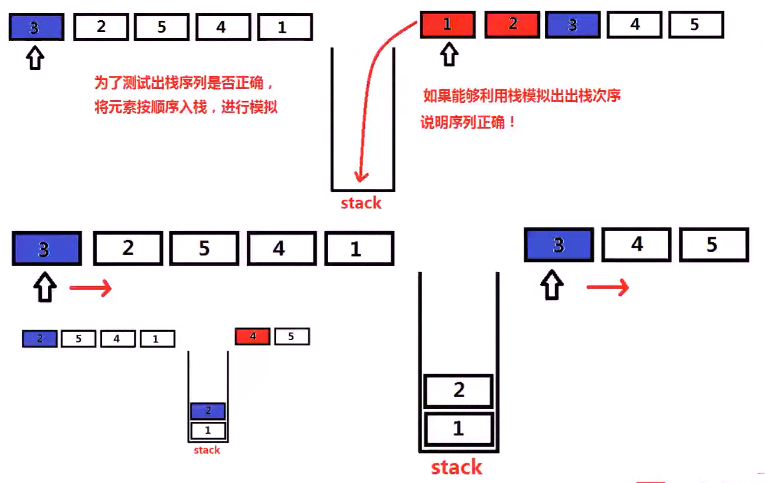
现在要检测 3 2 5 4 1 是否合法？

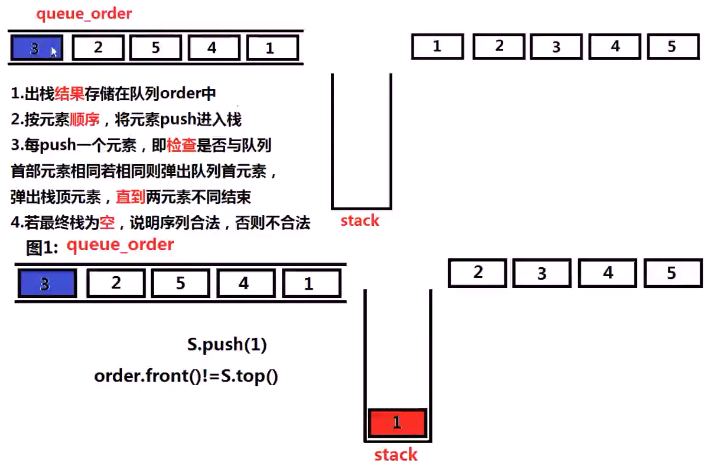
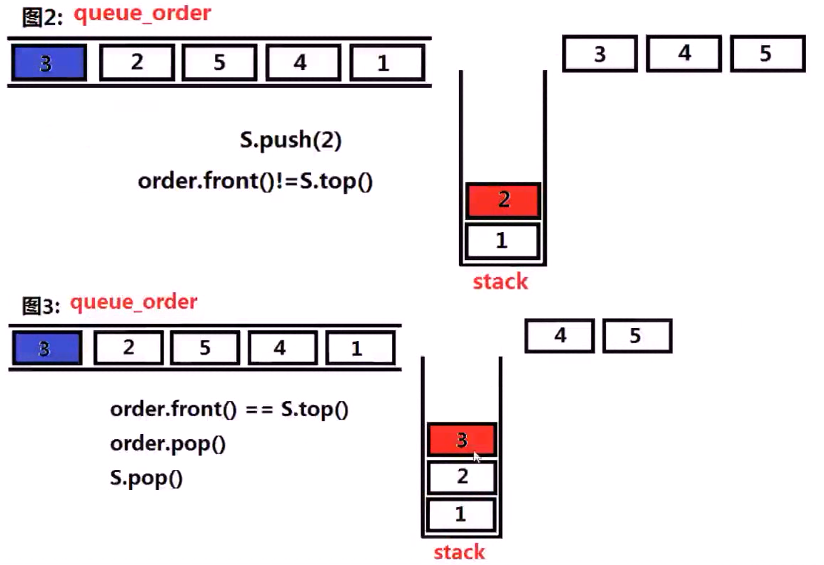
这时3 就和队列中的第一个相等了，此时栈和队列同时进行弹出操作！

继续对比！

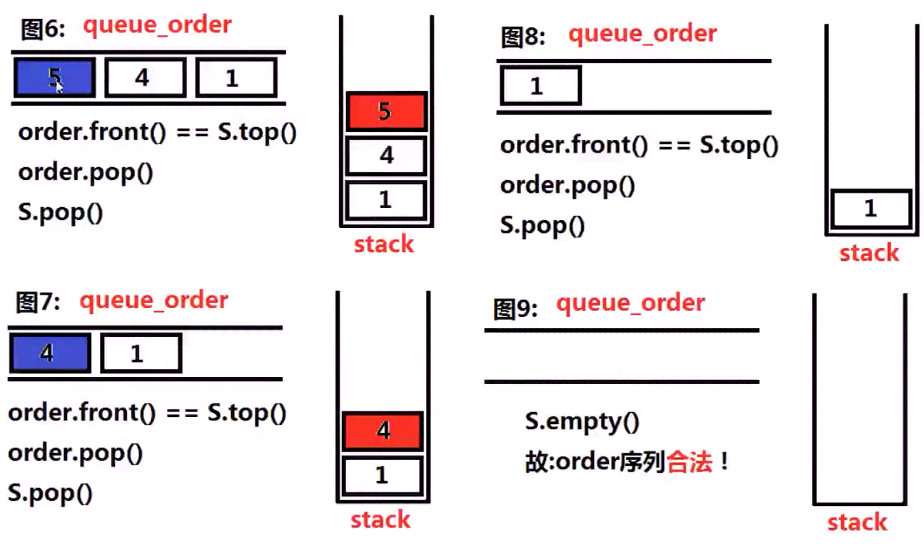
最后栈中的元素为空，所以说明合法，否则是不合法的！

下面是个不合法序列的举例：

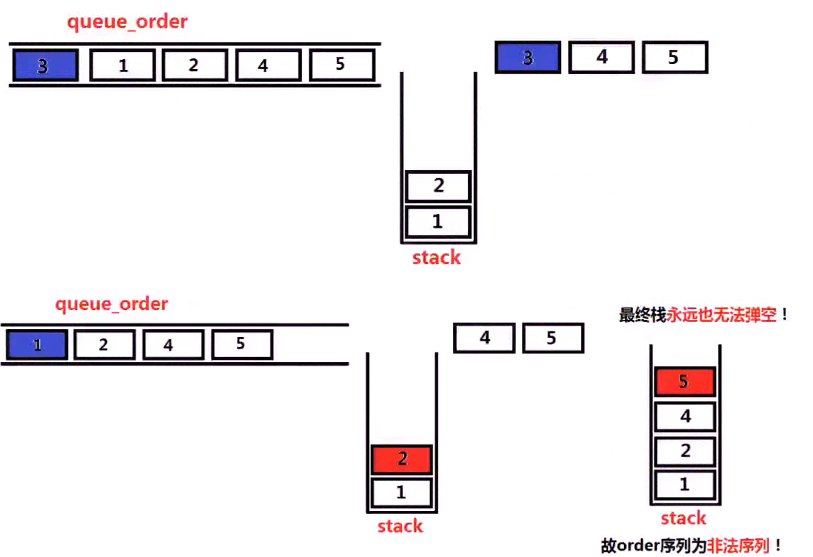
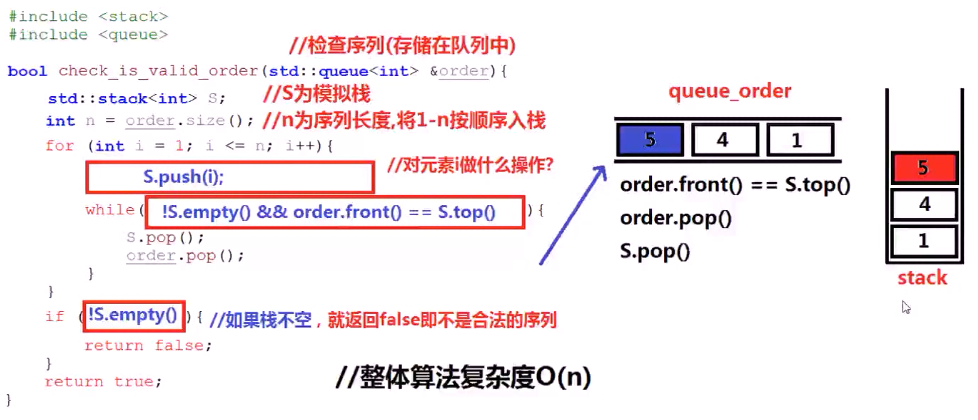
虽然它是有两个循环，但是它整体的时间复杂度还是O(n) ,因为每个元素都是入栈一次和出栈一次！

 1 bool check_is_valid_order(queue<int> &que_order){
 2     stack <int> stk;  //模拟栈
 3     int n = que_order.size();
 4     for (int i = 0; i < n; ++i) {
 5         stk.push(i+1);
 6         while (!stk.empty() &&stk.top() == que_order.front()){
 7             stk.pop();
 8             que_order.pop();
 9         }
10     }
11     if(!stk.empty()){  //当stk 模拟战不是空的时候，说明不合法
12         return false;
13     }
14     return true;
15 }

View Code

POJ的提交：

 1 #include <iostream>
 2 using namespace std;
 3 
 4 #include <stack>
 5 #include <queue>
 6 bool check_is_valid_order(queue<int> &que_order){
 7     stack <int> stk;  //模拟栈
 8     int n = que_order.size();
 9     for (int i = 0; i < n; ++i) {
10         stk.push(i+1);
11         while (!stk.empty() &&stk.top() == que_order.front()){
12             stk.pop();
13             que_order.pop();
14         }
15     }
16     if(!stk.empty()){  //当stk 模拟战不是空的时候，说明不合法
17         return false;
18     }
19     return true;
20 }
21 
22 
23 int main(){
24     int n;
25     int train;
26     scanf("%d",&n);
27     while(n){
28         scanf("%d",&train);
29         while(train){
30             queue <int> order;
31             order.push(train);
32             for (int i = 1; i < n; ++i) {
33                 scanf("%d",&train);
34                 order.push(train);
35             }
36             if(check_is_valid_order(order)){
37                 cout<<"Yes"<<endl;
38             }else{
39                 cout<<"No"<<endl;
40             }
41             scanf("%d",&train);
42         }
43         cout<<endl;
44         scanf("%d",&n);
45     }
46     return 0;
47 }

POJ提交代码！！！

例5：简单的计算器(No.224 leetcode )：

思路及代码：

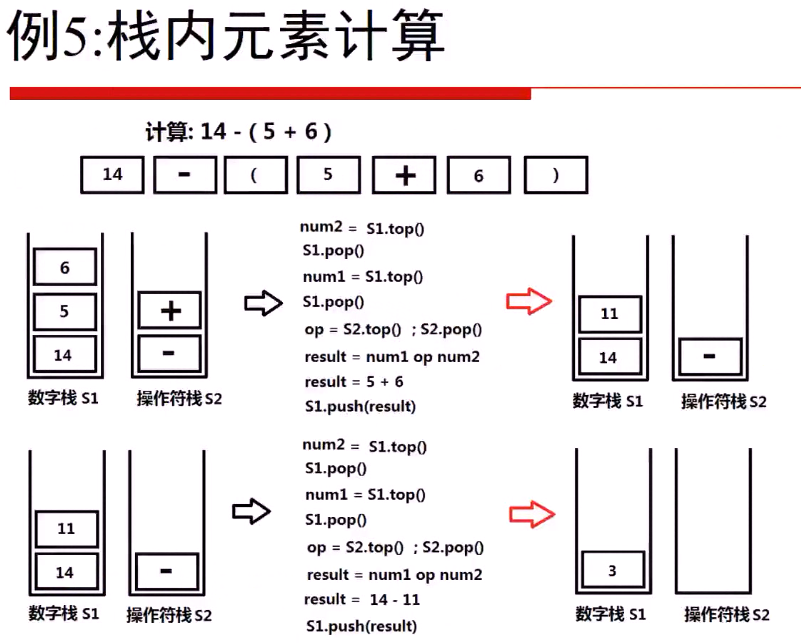
下面是没有优先级（无括号）和有优先级（有括号）的对比

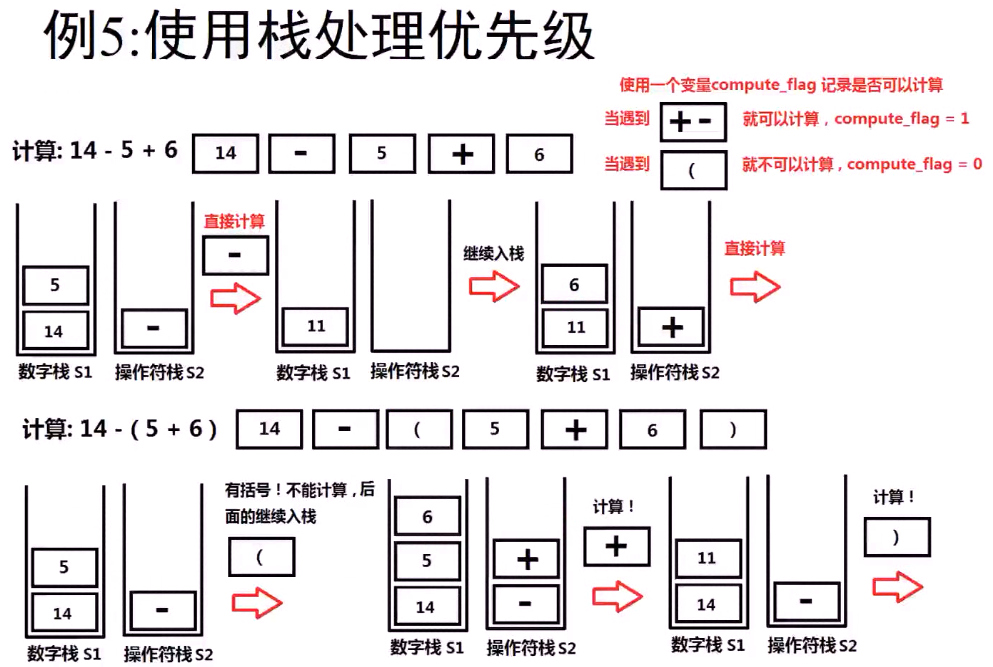
下面是一个例子来说明思路！！！

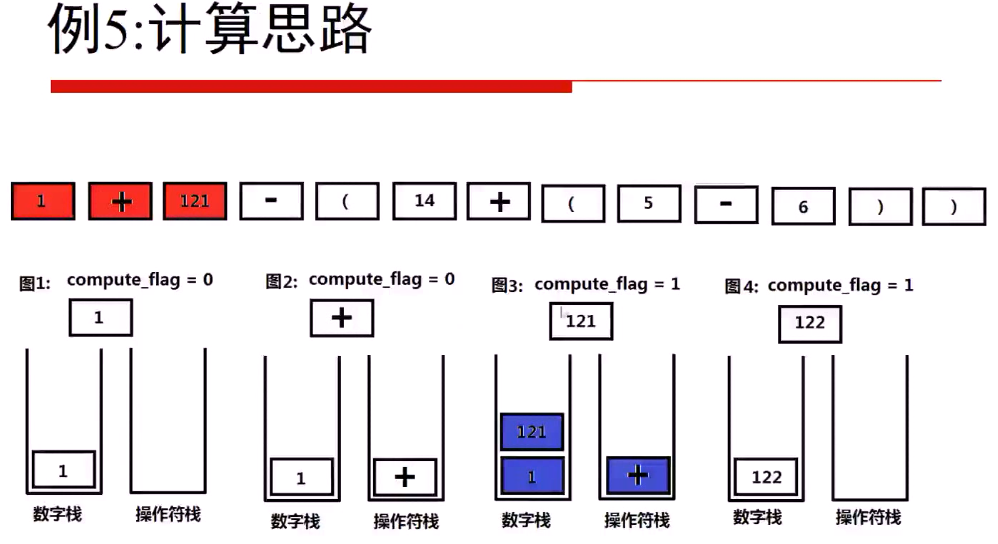
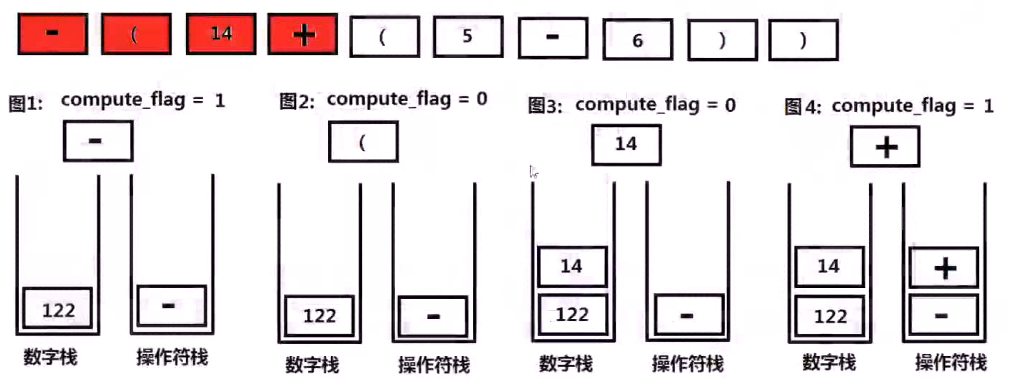
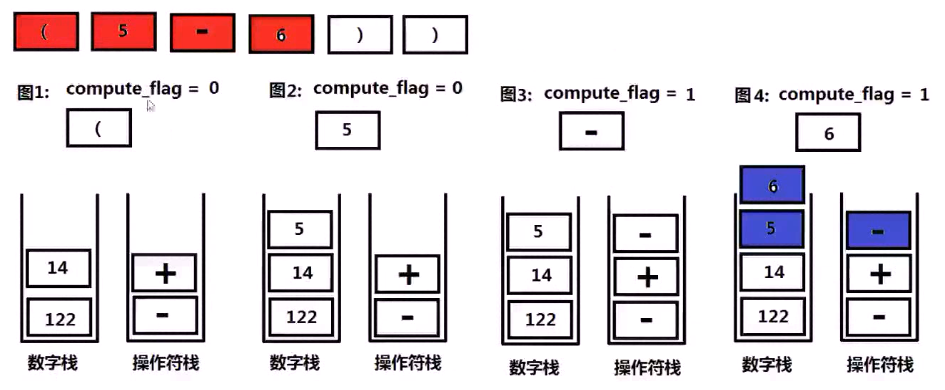
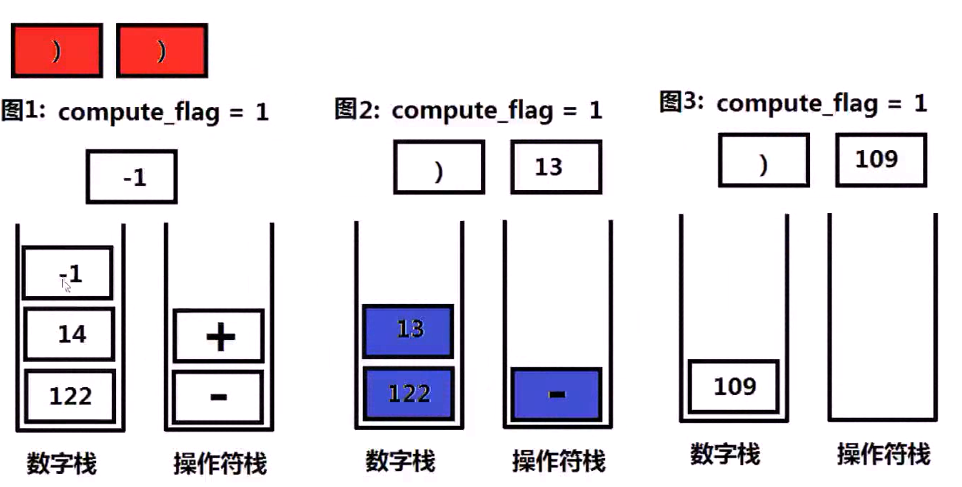
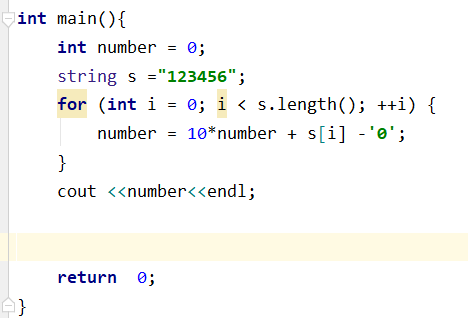
下面的问题是字符串如何转换成数字？

计算函数：

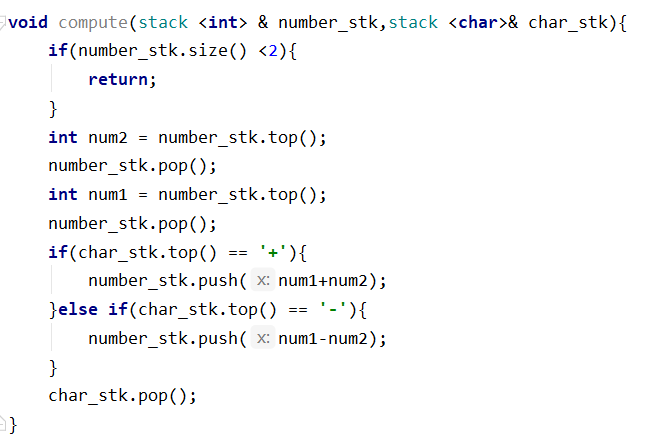
 1 void compute(stack <int> & number_stk,stack <char>& char_stk){
 2     if(number_stk.size() <2){
 3         return;
 4     }
 5     int num2 = number_stk.top();
 6     number_stk.pop();
 7     int num1 = number_stk.top();
 8     number_stk.pop();
 9     if(char_stk.top() == '+'){
10         number_stk.push(num1+num2);
11     }else if(char_stk.top() == '-'){
12         number_stk.push(num1-num2);
13     }
14     char_stk.pop();
15 }

每次的计算函数

下面是最重要的字符串处理的思路：

状态机！！！

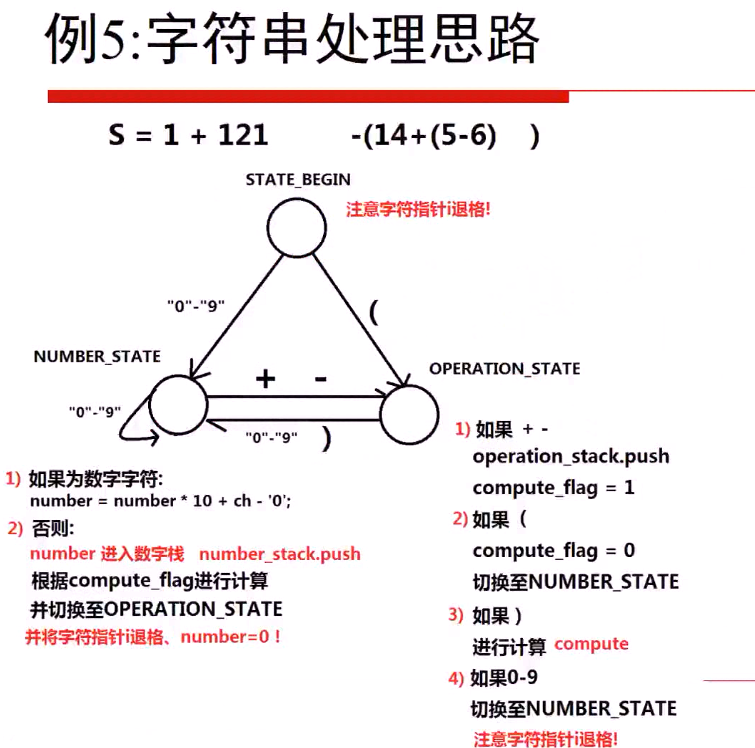
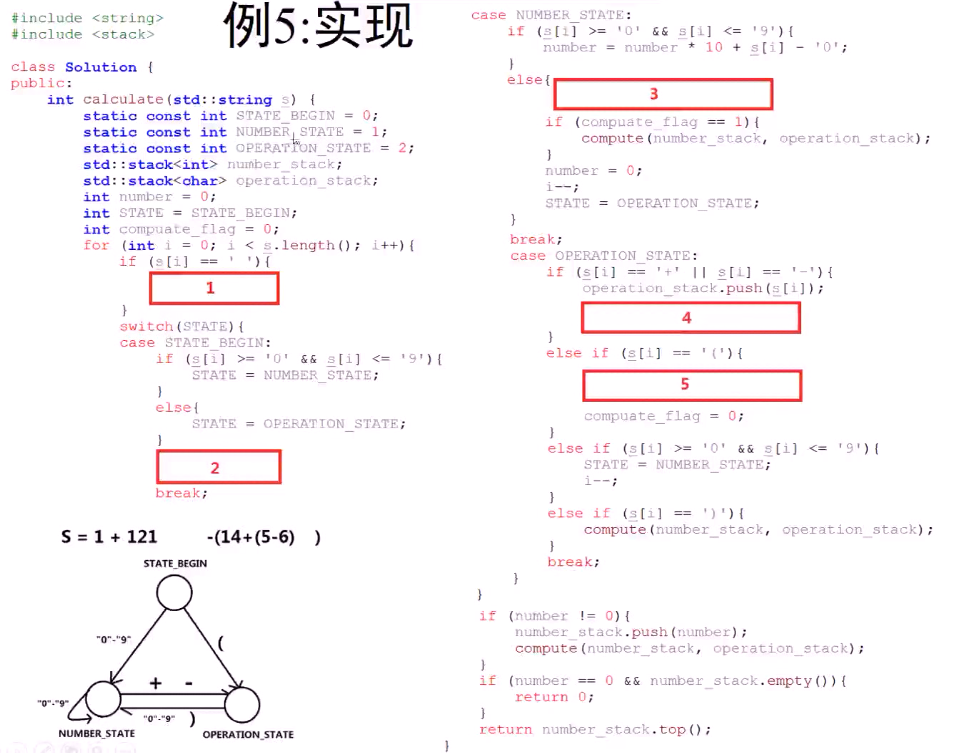
 1 void compute(stack <long> & number_stk,stack <char>& operation_stk){
 2     if(number_stk.size() <2){
 3         return;
 4     }
 5     long num2 = number_stk.top();
 6     number_stk.pop();
 7     long num1 = number_stk.top();
 8     number_stk.pop();
 9     if(operation_stk.top() == '+'){
10         number_stk.push(num1+num2);
11     }else if(operation_stk.top() == '-'){
12         number_stk.push(num1-num2);
13     }
14     operation_stk.pop();
15 }
16 
17 class Solution{
18 public:
19     long calculate(string s){
20         static const int STATE_BEGIN =0;
21         static const int NUMBER_STATE =1;
22         static const int OPERATION_STATE =2;
23 
24         stack <long> number_stk;
25         stack <char> operation_stk;
26 
27         long number =0;
28         int STATE = STATE_BEGIN;
29         int compuate_flag = 0;
30         for (int i = 0; i < s.length(); ++i) {
31             if(s[i] == ' '){ //如果第一个字符是空格
32                 continue;
33             }
34             switch(STATE){
35                 case STATE_BEGIN:
36                     if(s[i] >='0' && s[i] <='9'){
37                         STATE = NUMBER_STATE;
38                     }else{
39                         STATE = OPERATION_STATE;
40                     }
41                     //i 指针回退操作
42                     i -- ;
43                     break;
44                 case NUMBER_STATE:
45                     if(s[i] >='0' && s[i] <='9') {
46                         number = 10*number + s[i] -'0';
47                     }else{
48                         number_stk.push(number);  //将算好的number push到栈中
49                         if(compuate_flag == 1){
50                             compute(number_stk,operation_stk);
51                         }
52                         number = 0;
53                         i--;
54                         STATE = OPERATION_STATE;
55                     }
56                     break;
57                 case OPERATION_STATE:
58                         if(s[i] == '+' || s[i] == '-'){
59                             operation_stk.push(s[i]);
60                             compuate_flag = 1;  //当遇到 + / - 时候 为1
61                         }else if(s[i] == '('){
62                             // 遇到 （ 
63                             STATE = NUMBER_STATE;
64                             compuate_flag = 0;
65                         }else if(s[i]>='0' && s[i] <='9'){
66                             i--;  //当仍然遇到的是数字时候。  回退
67                             STATE = NUMBER_STATE;
68                         }else if(s[i] == ')'){
69                             compute(number_stk,operation_stk); //计算最后一步
70                         }
71                     break;
72             }
73 
74         } //for
75         if(number != 0){  //1+2+3  就会剩一个number = 3
76             number_stk.push(number);
77             compute(number_stk,operation_stk);
78         }
79         if(number==0 && number_stk.empty()){
80             return 0;   //例如给定字符串 “”
81         }
82         return number_stk.top();
83      }
84 };

LeetCode 代码

 1 #include <iostream>
 2 using namespace std;
 3 
 4 #include <stack>
 5 #include <queue>
 6 
 7 void compute(stack <int> & number_stk,stack <char>& operation_stk){
 8     if(number_stk.size() <2){
 9         return;
10     }
11     int num2 = number_stk.top();
12     number_stk.pop();
13     int num1 = number_stk.top();
14     number_stk.pop();
15     if(operation_stk.top() == '+'){
16         number_stk.push(num1+num2);
17     }else if(operation_stk.top() == '-'){
18         number_stk.push(num1-num2);
19     }
20     operation_stk.pop();
21 }
22 
23 class Solution{
24 public:
25     long calculate(string s){
26         static const int STATE_BEGIN =0;
27         static const int NUMBER_STATE =1;
28         static const int OPERATION_STATE =2;
29 
30         stack <int> number_stk;
31         stack <char> operation_stk;
32 
33         int number =0;
34         int STATE = STATE_BEGIN;
35         int compuate_flag = 0;
36         for (int i = 0; i < s.length(); ++i) {
37             if(s[i] == ' '){ //如果第一个字符是空格
38                 continue;
39             }
40             switch(STATE){
41                 case STATE_BEGIN:
42                     if(s[i] >='0' && s[i] <='9'){
43                         STATE = NUMBER_STATE;
44                     }else{
45                         STATE = OPERATION_STATE;
46                     }
47                     //i 指针回退操作
48                     i -- ;
49                     break;
50                 case NUMBER_STATE:
51                     if(s[i] >='0' && s[i] <='9') {
52                         number = 10*number + s[i] -'0';
53                     }else{
54                         number_stk.push(number);  //将算好的number push到栈中
55                         if(compuate_flag == 1){
56                             compute(number_stk,operation_stk);
57                         }
58                         number = 0;
59                         i--;
60                         STATE = OPERATION_STATE;
61                     }
62                     break;
63                 case OPERATION_STATE:
64                         if(s[i] == '+' || s[i] == '-'){
65                             operation_stk.push(s[i]);
66                             compuate_flag = 1;  //当遇到 + / - 时候 为1
67                         }else if(s[i] == '('){
68                             // 遇到 （  STATE_BEGIN
69 //                            STATE = STATE_BEGIN;
70                             STATE = NUMBER_STATE;  //它不能解决两个  (( 在一起 的情况，上面的可以解决。  
71                             compuate_flag = 0;
72                         }else if(s[i]>='0' && s[i] <='9'){
73                             i--;  //当仍然遇到的是数字时候。  回退
74                             STATE = NUMBER_STATE;
75                         }else if(s[i] == ')'){
76                             compute(number_stk,operation_stk); //计算最后一步
77                         }
78                     break;
79             }
80 
81         } //for
82         if(number != 0){  //1+2+3  就会剩一个number = 3
83             number_stk.push(number);
84             compute(number_stk,operation_stk);
85         }
86         if(number==0 && number_stk.empty()){
87             return 0;   //例如给定字符串 “”
88         }
89         return number_stk.top();
90      }
91 };
92 
93 
94 int main(){
95     string s = "1 -((1+10))";
96     Solution * solve = new Solution();
97     cout << solve->calculate(s);
98     return  0;
99 }

本地

堆方面：

预备知识：二叉堆属性

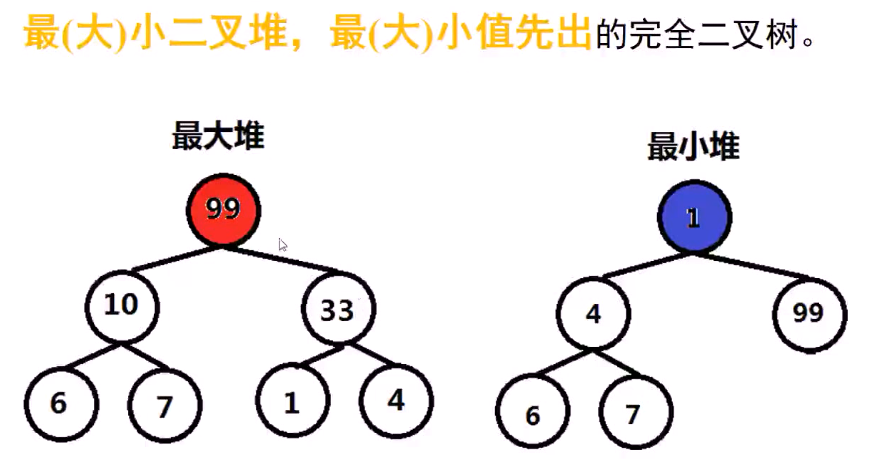
#include <iostream>
#include <queue> // for

using namespace std;

/*
// 打印堆里面的存的 数据
// 层级N = (int)log2(size) + 1
// 最后一层的个数 :num = size - 2^(N-1)
void printDataInHeap(priority_queue<int>& queue){


}
*/

void print(priority_queue<int>& heap){
    cout << "item: ";
    while(!heap.empty()){
        int item = heap.top();
        cout <<" " <<  item;
        heap.pop();
    }
    cout << endl;
}


int main(){
    priority_queue<int> maxHeap; // 优先队列底层实现是堆  // 默认是最大堆
    priority_queue<int> minHeap; // 最小堆 乘-1 即可

    int arrs[] = {6,10,1,7,99,4,33};
    for(int item:arrs){
        maxHeap.push(item);
        minHeap.push(-1*item); // 取出的时候 也要乘-1
    }

    print(maxHeap);
    print(minHeap);


    return 0;
}

stl 中的优先队列（底层是堆实现）

打印堆：

https://www.cnblogs.com/noKing/p/7966272.html

View Code

例6：(No.215 )数组中的第K个最大元素：

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

思路及代码：

方法一：简单粗暴，使用c++ STL 的priority_queue,（底层是堆）

#include <iostream>
#include <vector>
#include <queue> // for priority_queue

using namespace std;

int findKthLargest(vector<int>& nums, int k) {

    priority_queue<int> maxHeap;
    for(auto it=nums.cbegin();it!=nums.cend();it++){
        maxHeap.push(*it);
    }
    for(int i=0;i<k-1;i++){
        maxHeap.pop();
    }

    return maxHeap.top();
}


int main(){
    
    vector<int> vec={3,2,1,5,6,4};
    cout <<  findKthLargest(vec,2) << endl;

    vector<int> vec2={3,2,3,1,2,4,5,5,6};
    cout <<  findKthLargest(vec2,4) << endl;


    return 0;
}

View Code

时间复杂度为：O(n)

方法二：简单粗暴，维护一个K大小的最小堆，

    priority_queue<int> minHeap; // 要 乘 -1  
    for(int i =0;i<(int)nums.size();i++){
        if(i<k){
            minHeap.push(-1*nums[i]);
        }else{
            // 其他只有当 新元素比 栈顶元素小 才能进来  
            int top = minHeap.top();
            if(top > -1*nums[i]){
                minHeap.pop();
                minHeap.push(-1*nums[i]);
            }
        }

    }

    return -1*minHeap.top();

View Code

例7：(No.295 )数据流的中位数：

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例：

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
进阶:

如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？
如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

思路及代码：

1，简单粗暴：使用c++ STL 的priority_queue,并结合vector 来恢复堆，

LeetCode 提交不通过，（超时）

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

class MedianFinder {
    private:
        priority_queue<int> pri_que;
        vector<int> popItems;
    
    public:
            /** initialize your data structure here. */
        MedianFinder() {
        }
            
        void addNum(int num) {
            pri_que.push(num);
        }
        void recover(){
            // 恢复 pri_que 
            for(auto it = popItems.cbegin();it!= popItems.cend();it++){
                pri_que.push(*it);
            }
            popItems.clear();
        }
            
        double findMedian() {

            int size = pri_que.size();
            if(size %2 ==0 ){
                int cnt = size/2 - 1;
                for(int i=0;i<cnt;i++){
                    popItems.push_back(pri_que.top());
                    pri_que.pop();
                }
                int a = pri_que.top();
                popItems.push_back(a);
                pri_que.pop();
                int b = pri_que.top();


                recover();
                return (a+b)/2.0 ;
            }else{
                for(int i=0;i<size/2;i++){
                    popItems.push_back(pri_que.top());
                    pri_que.pop();
                }

                int ret = pri_que.top();
                recover();
                return ret;
            }
        }
        
};

int main(){

    MedianFinder* obj = new MedianFinder();
    obj->addNum(1);
    obj->addNum(2);
    double res = obj->findMedian();
    cout << res<< endl;

    obj->addNum(5);
    res = obj->findMedian();
    cout << res<< endl;



    return 0;
}

View Code

2，搞两个堆，一个最大堆，一个最小堆，各存一半数据（最多差一）而且要满足最大堆的堆顶比最小堆的堆顶小，

/*
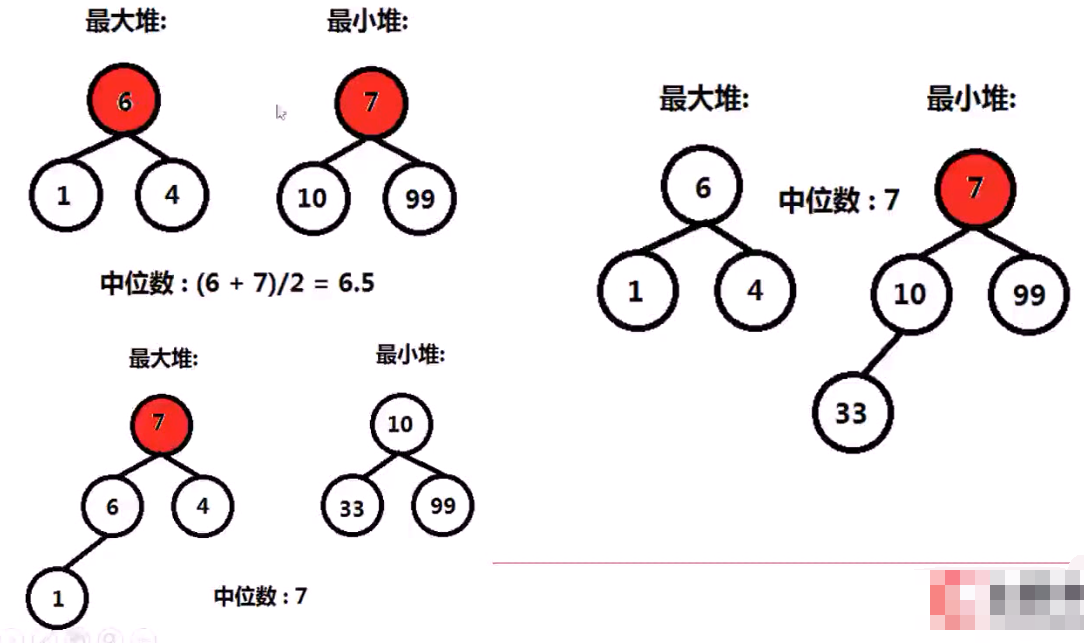
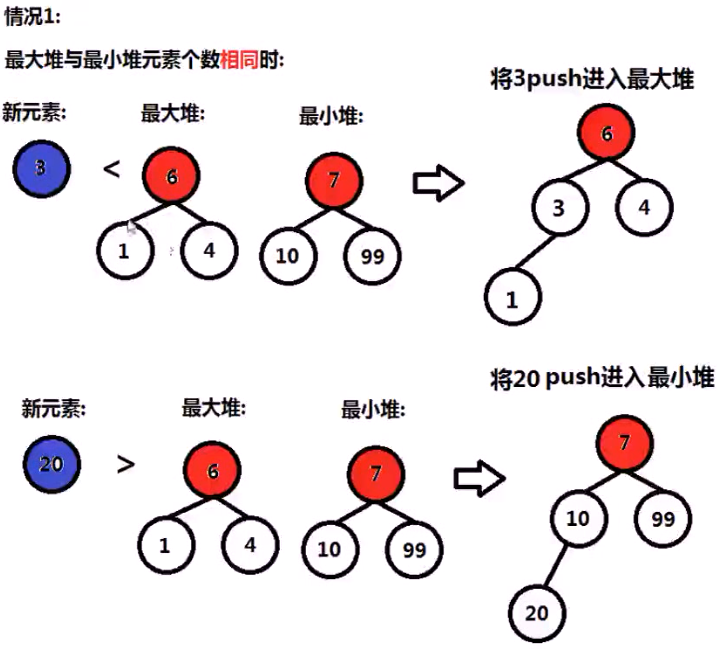
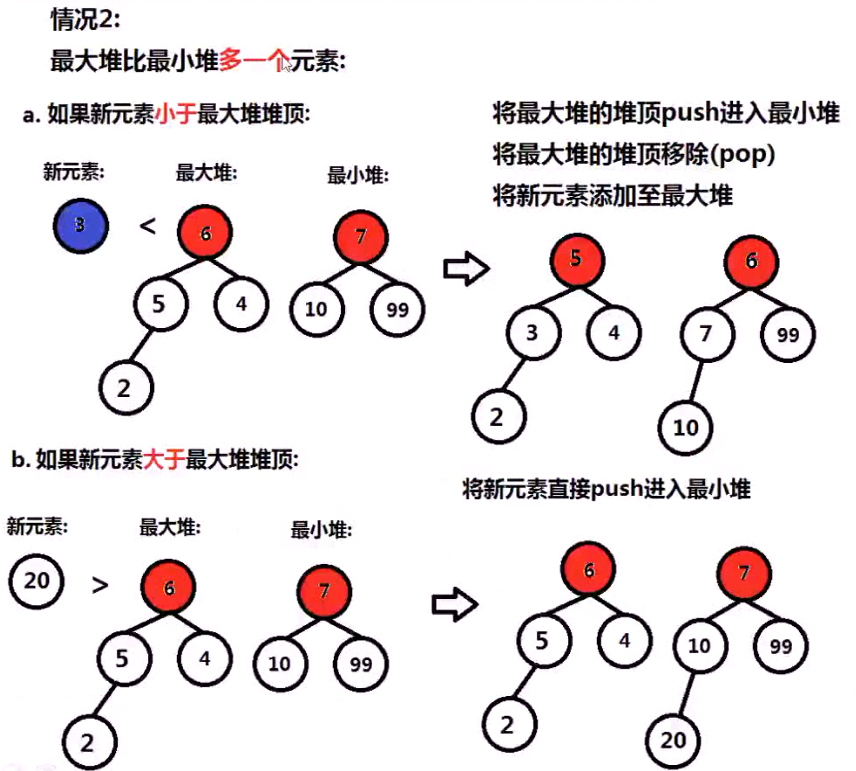
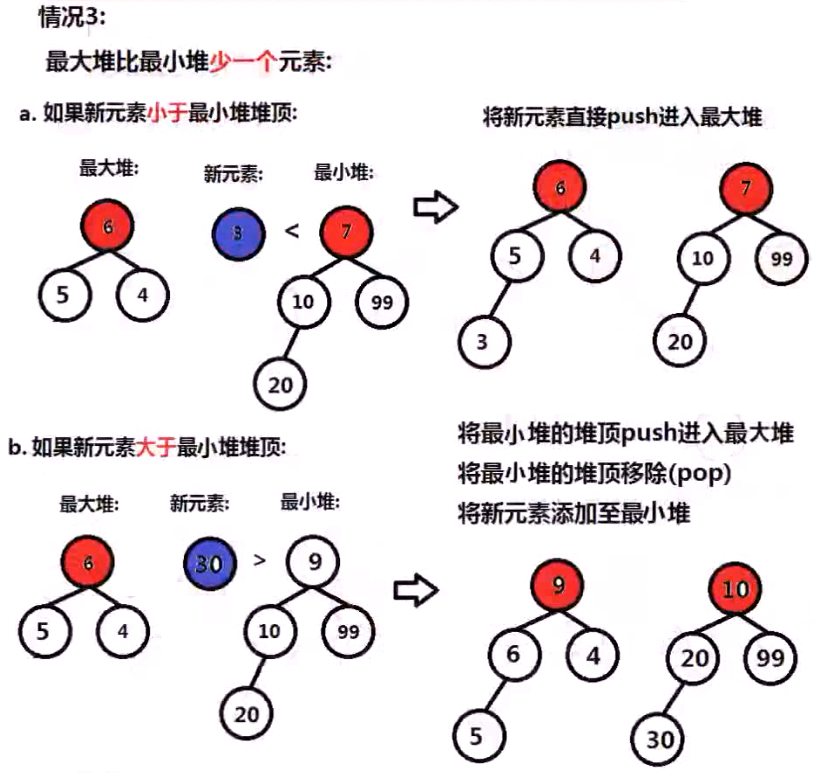
 * 1,最大堆的堆顶 比 最小堆的堆顶小  
 * 2,两个堆数目差距不能大于1  
 * */

class MedianFinder {
    private:
        priority_queue<int> maxHeap;
        priority_queue<int,vector<int>,greater<int>> minHeap;
    
    public:
            /** initialize your data structure here. */
        MedianFinder() {
        }
        void addNum(int num) {
            int maxSize = maxHeap.size();
            int minSize = minHeap.size();

            if(maxSize == 0){
                maxHeap.push(num);
                return;
            }

            // 三种情况  
            if(maxSize == minSize){ 
                if(num > maxHeap.top()){// 以最大堆 为标准 
                    minHeap.push(num);
                }else{
                    maxHeap.push(num);
                }

            }else if(maxSize > minSize){ 
                if(num > maxHeap.top()){// 以最大堆 为标准 
                    minHeap.push(num);
                }else{
                    minHeap.push(maxHeap.top());
                    maxHeap.pop();
                    maxHeap.push(num);
                }
            }else{
                if(num < minHeap.top()){ // 以最小堆 为标准了 
                    maxHeap.push(num);
                }else{
                    maxHeap.push(minHeap.top());
                    minHeap.pop();
                    minHeap.push(num);
                }
            }

        }
        double findMedian() {
            int maxSize = maxHeap.size();
            int minSize = minHeap.size();

            cout << maxSize<< " " << minSize<< endl;
            if(maxSize == minSize){
                return (maxHeap.top()+minHeap.top())/2.0;
            }else if(maxSize < minSize ){
                return minHeap.top();
            }else{
                return maxHeap.top();
            }
        }
        
};

View Code

例8：(No. )：

思路及代码：

posted @ 2019-11-03 17:14 Zcb0812 阅读(189) 评论(0) 收藏举报

刷新页面返回顶部

A 第二课 栈_队列_堆

内容概览及预备知识：

预备知识：栈与队列：

STL基本的栈操作(stack)：

STL基本的队列操作（queue）：

例1：使用队列实现栈 （No.225）：

思路及代码：

例2：使用栈实现队列 （No.232）：

例3：包含min函数的栈（No.155）：

思路及代码：

例4：合法的出栈序列（poj.1363）：

思路及代码：

例5：简单的计算器(No.224 leetcode )：

思路及代码：

堆方面：

预备知识：二叉堆属性

打印堆：

例6：(No.215 )数组中的第K个最大元素：

思路及代码：

例7：(No.295 )数据流的中位数：

思路及代码：

例8：(No. )：

思路及代码：

公告

A 第二课栈_队列_堆

例1：使用队列实现栈（No.225）：

例2：使用栈实现队列（No.232）：