luoguP4322【[JSOI2016]最佳团体】题解

传送门

思路：看到这种求一个比值的题，很容易能想到01分数规划（其实就是二分） \(+\) 树上 \(\mathrm{DP}\)

题目要我们求的是 \(\dfrac{\sum{p_i}}{\sum{s_i}}\) 的最大值

我们设 \(mid\) 为正确答案，要使 \(\dfrac{\sum{p_i}}{\sum{s_i}}\) 的值最大，则有：

\[\dfrac{\sum{p_i}}{\sum{s_i}} \leqslant mid \]

移项整合得到：

\[mid \cdot \sum{s_i}- \sum{p_i} \geqslant \mathrm{0} \]

用二分来求 \(mid\) 的值，若 \(check(mid)\) 成立，则 \(l=mid\) 。

但是如何做 \(check\) ？

将题目转换成一棵树，如图：

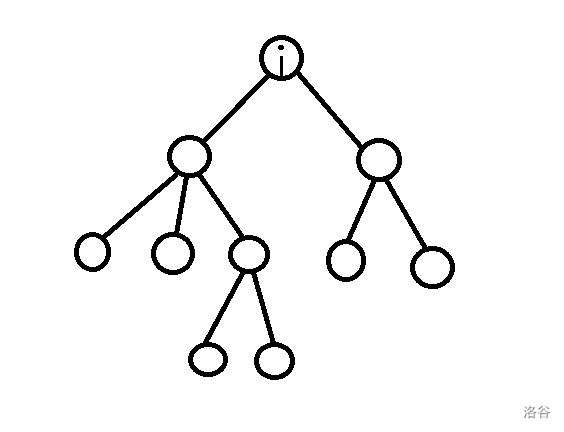
对于每一个点 \(i\) ，因为要求的是 \(\dfrac{\sum{p_i}}{\sum{s_i}}\) ，所以将它的值 \(d[i]\) 转换成 \(p[i]-s[i] \times mid\) 。

再从 \(0\) 号点开始用 \(dfs\) 来 \(DP\) 。

用 \(dp[i][j]\) 表示在以 \(i\) 为根的子树中选出 \(j\) 个点的最大性价比，最终得出的结果为 \(dp[0][k+1]\) （注意这里是 \(k+1\) ，因为要加上 \(0\) 号点）。

那么状态转移方程是什么呢？

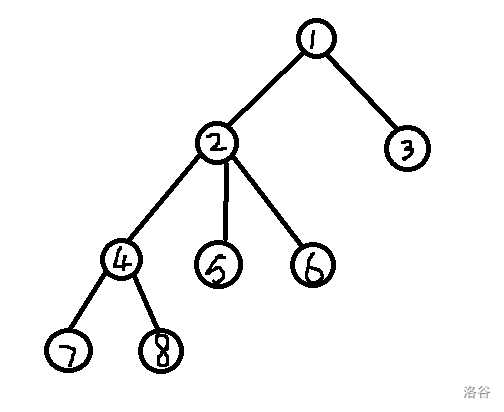
对于如图的一棵树，以结点 \(2\) 为例，
想要求 \(dp[2][j]\) ，它的值取决于它的子树 \(4\)，\(5\)，\(6\) 的 \(dp\) 的值。

所以 \(2\) 的 \(dp\) 值为它的每棵子树的一部分的性价比最大值，这 “一部分” 由枚举解决。

所以得出方程：

\[dp[u][j]=\max(dp[u][j],dp[v][k]+dp[u][j-k]) \]

时间复杂度为 \(O(n^2)\) 具体怎么算可以参考网上的博客。

代码如下：

#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
#define cmax(a,b) a=a>b?a:b
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(!isdigit(c)&&c!='-') c=getchar();
	if(c=='-') f=-1;
	while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
	return x*f;
}
const int N=2502;
struct edge{
	int to,next;
}e[N<<1];
const float ex=1e-4;
int tot,k,n,h[N],sz[N];
float dp[N][N],d[N],p[N],s[N];
inline void add(int x,int y){
	e[++tot]=(edge){y,h[x]};
	h[x]=tot;
}
void dfs(int x,int fa){
	sz[x]=1,dp[x][1]=d[x];
	for(register int i=h[x];i;i=e[i].next){
		int y=e[i].to;
		if(y==fa) continue;
		dfs(y,x);
		sz[x]+=sz[y];
		for(register int j=min(k+1,sz[x]);j;j--){
			int minn=min(j-1,sz[x]);
			for(register int z=1;z<=minn;z++){
				cmax(dp[x][j],dp[y][z]+dp[x][j-z]);
			}
		}
	}
}
inline bool check(float m){
	for(register int i=1;i<=n;i++){
		d[i]=p[i]-s[i]*m;
	}
	for(register int i=0;i<=n;i++){
		for(register int j=1;j<=k+1;j++){
			dp[i][j]=-2147483647;
		}
	}
	dfs(0,-1);
	return dp[0][k+1]>=0;
}
int main(){
	cin>>k>>n;
	float l=0,r=0;
	for(register int i=1;i<=n;i++){
		s[i]=read(),p[i]=read();
		cmax(r,p[i]); 
		add(read(),i);
	}
	while(r-l>ex){
		float mid=(l+r)/2;
		if(check(mid)){
			l=mid;
		}else{
			r=mid;
		}
	}
	printf("%.3f",l);
	return 0;
}