DP 优化学习笔记

目录

• 决策单调性优化 DP

决策单调性优化 DP

斜率优化

解决形如这样的 DP 方程 \(f_i = \max (f_j + A_iB_j + C_i + D_j)\)，其中表示的 \(A_i\) 是和 \(i\) 有关的系数，其他同理。

如果没有 \(A_iB_j\) 这一项，我们可以轻松用单调队列解决，我们通过一道例题来引入这种优化。

【例题 1】P3195 [HNOI2008] 玩具装箱

读者不难写出动态规划方程如下：

\[f_i = \min \left ( f_j + (i - j - 1 + \sum_{k=i+1}^{j} c_k - L)^2 \right ) \]

其中 \(f_i\) 表示装下前 \(i\) 个物品的最小代价。

直接转移的时间复杂度是 \(\mathcal{O}(n^2)\) 的，不足以通过本题，我们需要一个 \(\mathcal{O}(n \log n)\) 甚至 \(\mathcal{O}(n)\) 的算法。我们来看看这个方程有什么特点，看到连续的求和，我们直接拆成前缀和，这个 \(\min\) 很重要，但是我们先省略不写。

此处记 \(s_x = \sum_{i=1}^{x} c_i\)。

然后可得：

\[f_i = f_j + (i - j - 1 + s_i - s_j - L)^2 \]

现在项有点多，首先把常数项合并，记 \(L \leftarrow L + 1\)，然后我们观察到有一些重复的东西，不妨记 \(a_x = x + s_x\)，则有：

\[f_i = f_j + (a_i - a_j - L)^2 \]

基础的转化到此结束。

我们去考虑 \(i\) 的两个决策点 \(x, y(x < y)\)，思考一下如果在后面的决策更优，式子是什么样的。

\[\begin{aligned} f_x + (a_i - a_x - L)^2 & \ge f_y + (a_i - a_y - L)^2\\ f_x + (a_i - L)^2 + a_x^2 - 2a_x(a_i - L) &\ge f_y + (a_i - L)^2 + a_y^2 - 2a_y(a_i - L)\\ f_x + a_x^2 - 2a_xa_i +2a_xL &\ge f_y + a_y^2 - 2a_ya_i +2a_yL\\ 2a_i(a_y - a_x)&\ge(f_y + a_y^2 + 2a_yL) - (f_x + a_x^2 + 2a_xL) \\ 2a_i&\ge \dfrac{(f_y + a_y^2 + 2a_yL) - (f_x + a_x^2 + 2a_xL)}{a_y - a_x}\\ \end{aligned} \]

这个结论的逆命题也成立，即当 \(x,y\) 对于某个 \(i\) 满足 \(2a_i\ge \dfrac{(f_y + a_y^2 + 2a_yL) - (f_x + a_x^2 + 2a_xL)}{a_y - a_x}\) 时，\(y\) 比 \(x\) 更优。

我们注意到 \(a_i = i + s_i\) 是单调递增的，也就是说，在我们从 \(1\) 到 \(n\) 枚举 \(i\) 时，这个 \(2a_i\) 是在不断变大的，我们想要的是一个最优的决策点，那么就可以使用单调队列维护这个东西，下文无特殊说明默认 \(q\) 为队列，\(h\) 为队头，\(t\) 为队尾。

假设当前有若干个决策点，我们依次加入这些决策点，每次加点前，按照上面的形式判断，直到队列中元素不足或者第一个元素是最优决策点，实际上我们就是不断地在做如下事情：

判断 \(h+1\) 是否比 \(h\) 更优，如果更优，弹出队头，重复上述操作，直至队列中只有一个元素或者不满足 \(h+1\) 比 \(h\) 更优。

这一步的正确性显然，因为 \(a_i\) 是递增的，那么现在如果有 \(h+1\) 比 \(h\) 更优，在之后的点一定也满足这一条件，更新答案，读者可以对照下文的代码理解一下。

点击查看代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

#define pf(x) ((x) * (x))
const int N = 100005;
int n, L, a[N], s[N], f[N], h, t, q[N];
double calc(int x, int y) {
    return (f[y] + pf(a[y]) + 2 * a[y] * L - f[x] - pf(a[x]) - 2 * a[x] * L) *
           1.0 / (a[y] - a[x]);
}
// 此 calc 函数还可以化简，但没必要
signed main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    cin >> n >> L;
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        s[i] += s[i - 1];
        a[i] = s[i] + i; // 和上文定义相同
    }
    L++;
    // 注意一开始 h = t = 0，还隐含了一个 0 的决策点（从头开始选）
    for (int i = 1; i <= n; i++) {
        while (h < t && calc(q[h], q[h + 1]) <= 2 * a[i])
            h++;
        f[i] = f[q[h]] + pf(a[i] - a[q[h]] - L); // 转移
        while (h < t && calc(q[t - 1], q[t]) >= calc(q[t], i))
            t--;
        q[++t] = i;
    }
    cout << f[n] << '\n';
    return 0;
}

很好，这种方法可以在比赛时快速推出条件，但是我们并没有涉及斜率优化 DP 的本质。

重新审视一下 \(f_i = f_j + A_iB_j + C_i + D_j\) 这个方程。我们将其稍稍变形，得到 \(f_i - C_i = B_jA_i + (f_j + D_j)\)，观察一下，把等式右边看作是一个关于 \(j\) 的一次函数，斜率为 \(B_j\)，截距为 \(f_j + D_j\)，我们要做的就是在当前所有直线中查询 \(x = A_i\) 时函数最大值或者最小值。

这会让人想到李超线段树，但用在这题未免大材小用，因为我们有很多性质，比如上文提到的 \(a_i\) 是单调的。

我们再换一种角度去理解它，这次换一种变形的方法，直接以【例题 1】的转移方程为例。

\[\begin{aligned} f_i & = f_j + a_i^2 + a_j^2 + L^2 - 2a_iL - 2a_ia_j + 2a_jL\\ f_i - (a_i - L) ^ 2 & = - 2a_ia_j + f_j + a_j^2 + 2a_jL\\ \underline{f_j + a_j^2 + 2a_jL}_y &= \underline{2a_i}_k\underline{a_j}_x + \underline{f_i - (a_i - L) ^ 2}_b \\ \end{aligned} \]

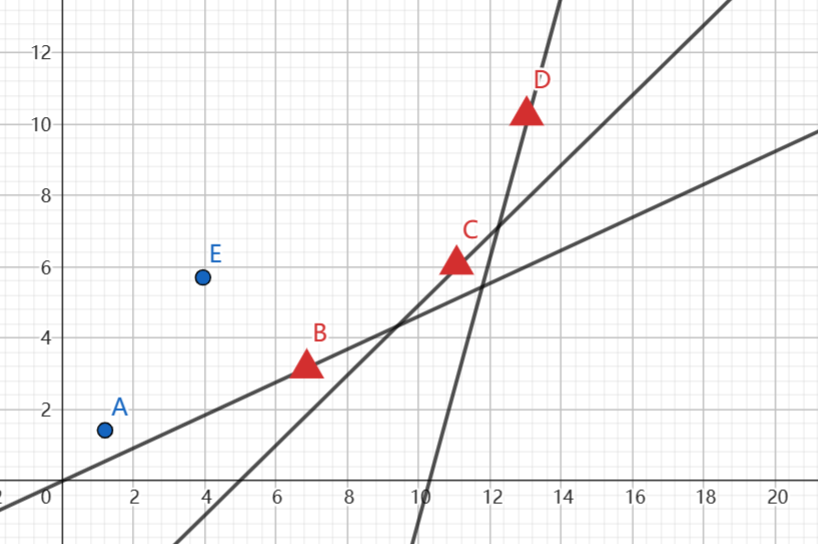
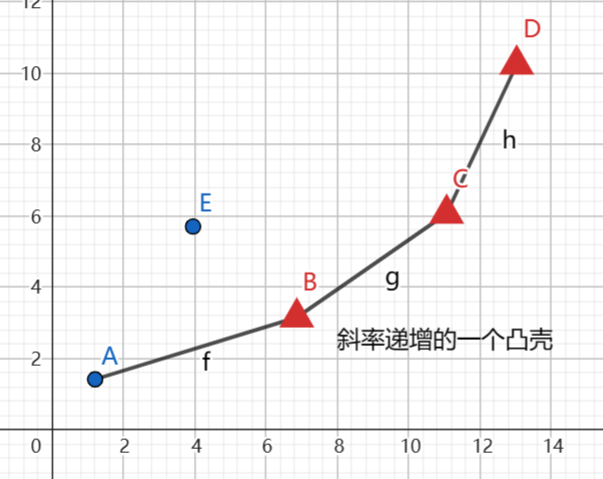
首先要明确一点，在转移 \(i\) 的时候，和 \(j\) 相关的量已经全都确定了，我们要求的就是当 \(k = 2a_i\)，也就是斜率一定时，经过 \((a_j, f_j + a_j^2 + 2a_jL)\) 的直线中截距最小（因为要取 min）的那个，如图所示，一开始我们的直线在 \(B\) 点处最优，那么因为 \(a_i\) 时递增的，也就是说我们的斜率也是递增的，那么之前的 \(A,E\) 两点都不再是最优的，可以删去，换句话说，我们最后会得到一个下凸壳。