微积分入门学习笔记
微积分入门学习笔记
前言:入门自 3b1b 【官方双语】微积分的本质。
导数
概念
首先要了解导数。
导数可以看作是一个函数在某个特定点的变化率,吗?
考虑我们对 \(f(x) = x ^ 2 - 6 x + 1\) 求导的时候,你会知道导函数是 \(f(x)'=2x - 6\),那么你带入一个值的时候,明明求的是一个点的值,哪里来的变化率呢?
所以,实际上导数求得的是函数在某个点切线的斜率,假如知道极限的思想,可以看作是两个非常非常接近的点,然后计算这两个点的变化率,可以看作是一个近似。
【思考】当一辆汽车以初速度为 \(0\),加速度为 \(1m/s^2\) 运动,那么请问车在第 \(0\) 秒,动了吗?
【解答】宏观上看,车子动了,但是假如得出 \(x-t\) 图像,并且求出 \(t=0\) 时的斜率,也就是速度为 \(0\),车子没动。
怎么回事呢?注意我上面说的近似,车子当然是动了,速度可能是 \(0.0000000001\),当然实际比这个小得多,近似为 \(0\) 而已。
求导
首先是多项式求导。
\(x^2\) 的导数是什么呢?
我们可以考虑一个正方形,边长为 \(x\),面积就是 \(x^2\),我们要清楚,研究 \(x^2\) 的导数,就是研究在 \(x\) 变化了极小的量的时候,\(x^2\) 变化的量。
我们记 \(x\) 变化了极小的量为 \(dx\), \(f(x)=x^2\) 变化了极小的量为 \(df\)。
现在考虑将这个正方形扩大 \(dx\) 的边长,那么面积增加了 \(2xdx + dx^2\),那么导数就是 \(\dfrac{df}{dx} = 2x + dx\),因为 \(dx\) 实在是太小了,可以忽略不计,那么就有了 \(\dfrac{df}{dx} = 2x\),即导数为 \(2x\)。
类似的,对于 \(x^3\) 考虑一个立方体的体积,更广泛的可以考虑代数证明。
我们知道了 \(x^m\) 的导数就是 \(mx^{m-1}\),当然对于负数也成立。
【思考】 \(\sqrt{x}\) 的导数。
【提示】考虑面积。
然后是三角函数的导数,尤其是 \(\sin,\cos\),你可以画出两者的图像。
首先考虑 \(\sin\)。
我们在单位圆上考虑,考虑当转过一个很小的角度的时候(就是很小的改变了 \(\sin\) 的值),答案如何变化。
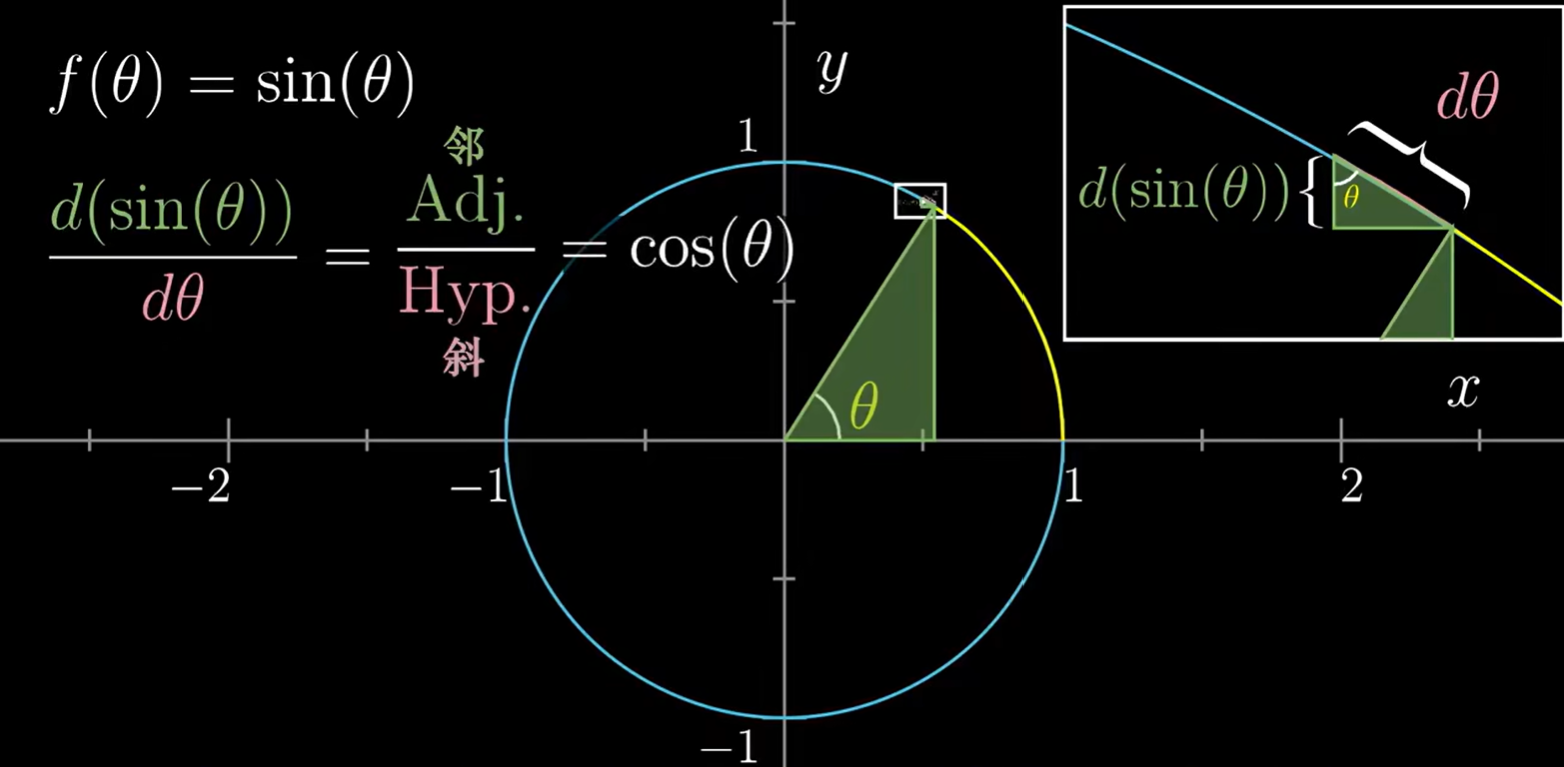
容易发现三角形 \(BCB_1\) 和 \(ABD\) 相似。
可得 \(∠BAD = ∠BB_1C\),那么根据三角函数的定义,容易得到 \(\sin\) 的导数就是 \(\cos\)!
类似的,有 \(\cos\) 的导数是 \(-\sin\)。
对于复杂函数,我们还有一些定则:
\(\dfrac{d}{dx}(f(x)+g(x)) = \dfrac{df}{dx} + \dfrac{dg}{dx}\)。
\(\dfrac{d}{dx}(f(x)g(x)) = f(x)\dfrac{dg}{dx} + g(x)\dfrac{df}{dx}\)。
\(\dfrac{d}{dx}(f(g(x))) = \dfrac{df}{dg}(g(x))\dfrac{dg}{dx}(x)\),这就是链式法则,自外向内一层层求导。
举个例子:
比如 \(\ln x^2 + 2x + 2\) 的导数就是先算 \(\ln f(x)\) 表示为 \(\dfrac{1}{f(x)}\),再乘上 \(f'(x)\) 表示为\(2x + 2\),那么原函数的导数就是 \(\dfrac{f'(x)}{f(x)}\)
还有分数求导,我们对 \(\dfrac{f(x)}{g(x)}\),导数就是 \(\dfrac{f(x)g'(x) + f'(x)g(x)}{g^2(x)}\)。
比如,对 \(\dfrac{1}{1 - x}\) 求 \(m\) 次导就可以得到 \(\dfrac{m!}{(1 - x) ^ {m + 1}}\)。
接着是指数求导。
例如 \(2^x\) 它的导数是什么?
我们回到定义,导数是一段极小的变化率的近似。
那么我们尝试知道当改变了极小的 \(dx\) 后的情况。实际上,导数就是 \(\dfrac{2^{x+dx}-2^x}{dx}=2^x\dfrac{2^{dx} - 1}{dx}\),有个很好的性质啊,也就是第二项和 \(x\) 无关了!
但是,似乎也不好算?不妨带入一个特殊的值,例如 \(dx=0.00000001\)。你会得到接近于 \(0.6931\) 的数字,这个有点太神秘了,对吗?
考察这个系数哪里来?你不妨在计算机里输入 \(\ln(2)\) 试试看。
类似的,你发现对于任意的 \(a ^ x\),导数都是 \(\ln(a)a^x\)。根据 \(\ln\) 的定义,我们知道 \(e^x\) 的导数是 \(e^x\),也就是它本身。
最后我们考虑一个隐函数的导数,所谓隐函数,大概就是 \(x^2 + y^ 2 = 25\),这样的函数,对于一个变量不一定有唯一的函数值。
这个函数的导数是什么?
答案是 \(2xdx + 2ydy = 0\),也就是 \(\dfrac{dy}{dx} = -\dfrac{x}{y}\)。
也就是在某个点的斜率是 \(\dfrac{-x}{y}\)。
简单的理解是变化率不变,也就是等式左右同时求导,结果仍然相等。
利用隐函数,我们可以通过一些已知函数的导数推出一些未知的导数。
比如 \(y=\ln(x)\),当然这是一个函数,但是假如我们不知道,可以将其看作是一个隐函数,我们还知道 \(e^x\) 的导数是 \(e^x\),对吧。
那么就有 \(e^y = x\),这就是自然对数的定义啊,对于两边同时求导,我们得到 \(e^y dy = dx\),也就是 \(\dfrac{dy}{dx} = \dfrac{1}{e^y} = \dfrac{1}{x}\)。
所以,\(\ln(x)\) 函数的导数就是 \(\dfrac{1}{x}\)。
此处还有一块内容:高阶导数。
你可以理解为对导数求导,生活中最常见的例子就是位移,速度,加速度,加加速度等等等等。
极限
举个例子,对于函数 \(y=\dfrac{\left(x+2\right)^{3}-8}{x}\),在 \(x = 0\) 的时候显然是无意义的,但是我们想要求得 \(\lim_{x \to 0}\dfrac{\left(x+2\right)^{3}-8}{x}\),那么可以不断逼近这个点,最后接近于 \(12\),我们就称作是“极限”。
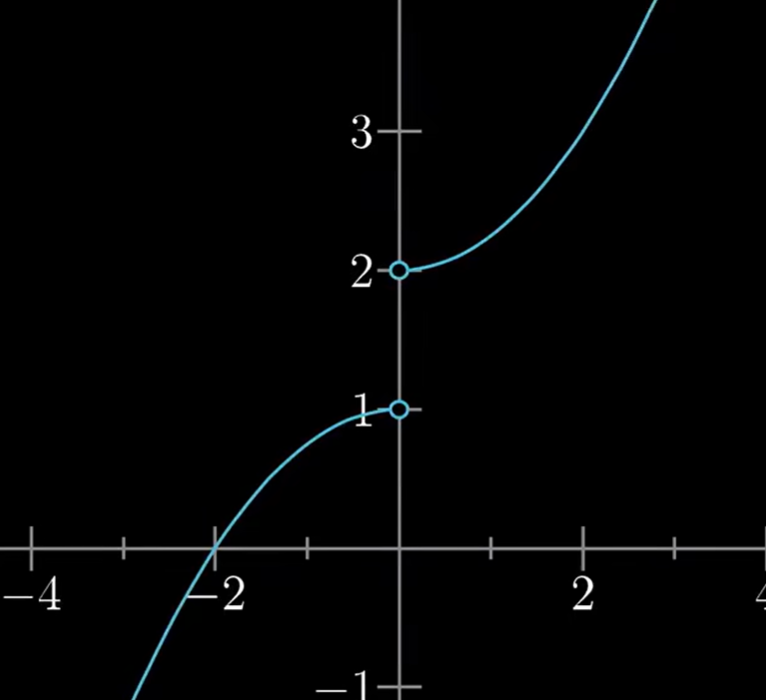
对于上图这样的情况,称零处的极限不存在。
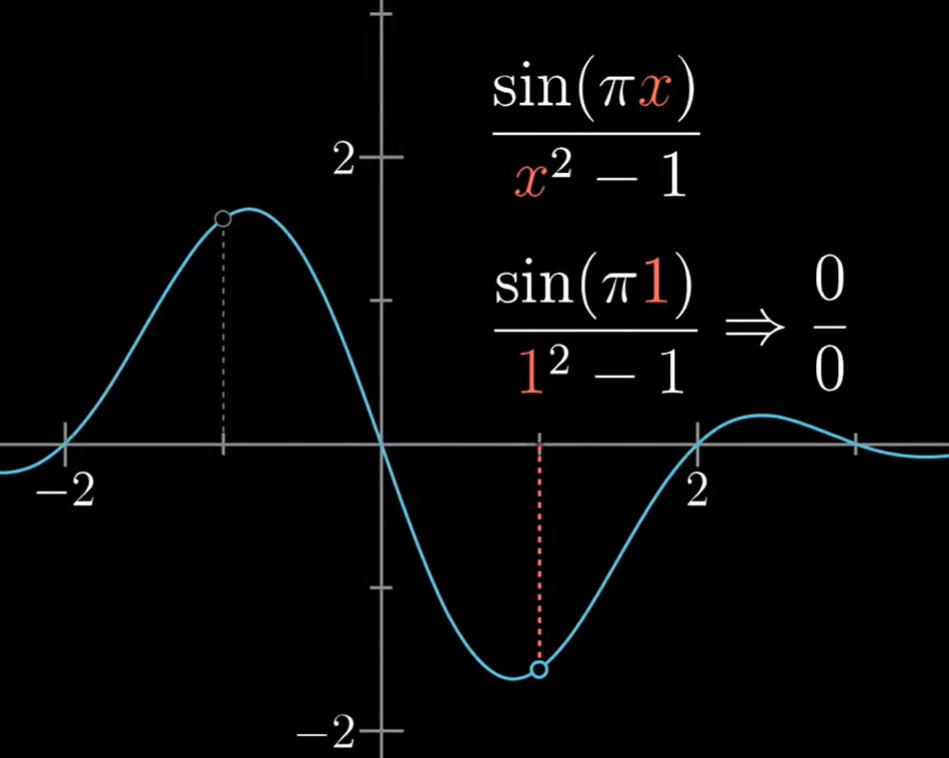
洛必达法则:
证明可以从微观的角度考虑。
积分
我们说积分是导数的逆运算。
导数是考虑对于极小的变化量 \(dx\),函数值的变化量,那么积分就是考虑根据函数的变化率,反推出函数的值。
举个例子,你在一辆车内,只能看到仪表盘,请问你如何知道车子经过了多远(假设直线运动)。
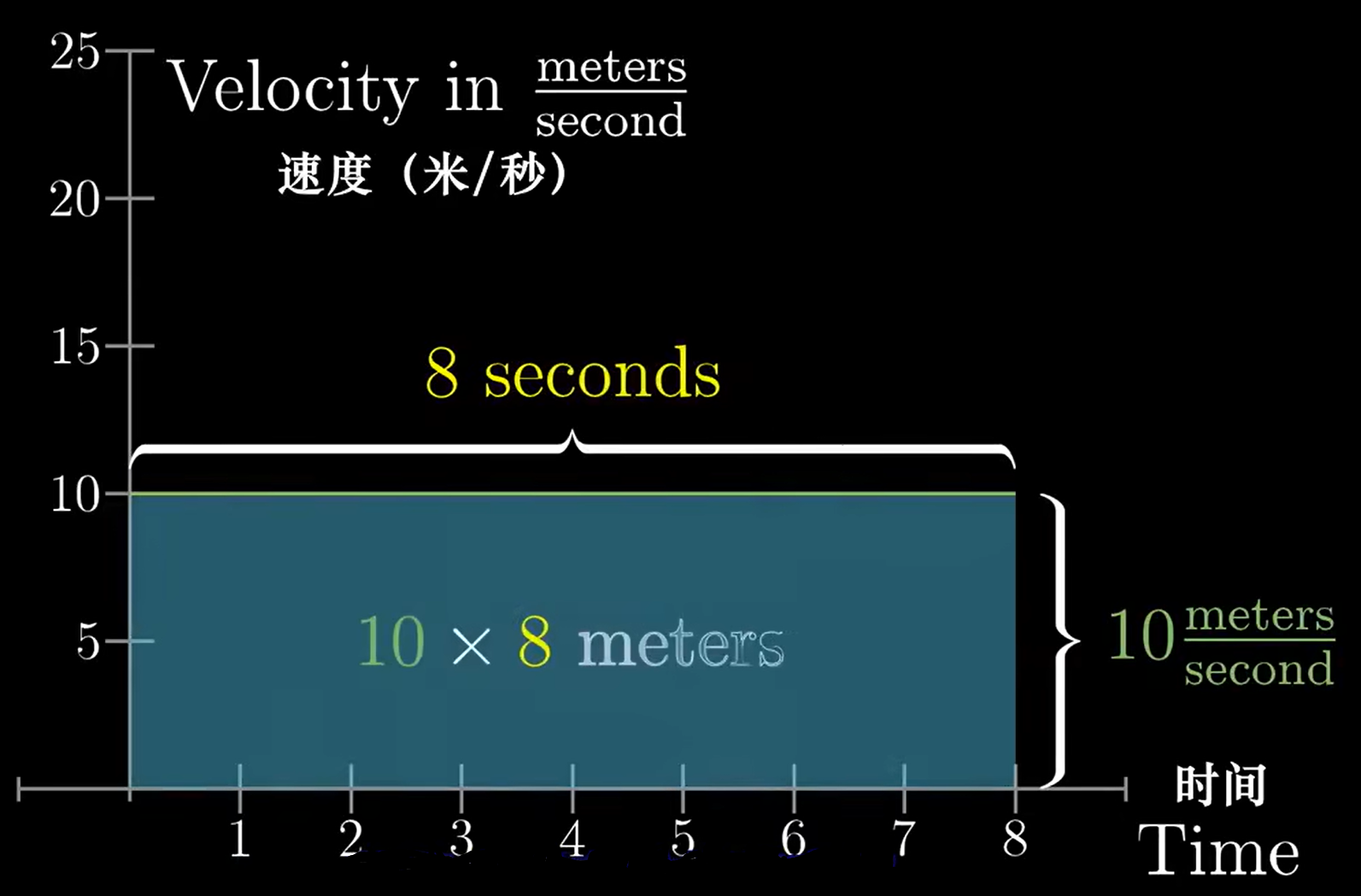
你看,要是匀速直线运动,就是求出这块面积,那么对于任何运动,也可以理解为求 \(v-t\) 图像曲线下方的面积。
尝试将时间按照很小的间隔分类,我们要求的实际上就是 \(v(t)dt\) 的和,只不过这里我们不用 \(\sum\) 表示,而是 \(\int\)。
这就是我们要求的东西,代表从 \(0\) 到 \(x\) 内车子通过的位移。
很好,求出来了,但是我们还不知道怎么算。
我们要知道的实际上是一块面积的计算,考虑当 \(dt\) 变化了一定的量后有:
实际上,我们有结论,一个函数下方的面积的导数等于这个函数本身。我们想知道这个面积的函数是什么,那么就是问,什么函数的导数等于当前的函数,那么就是对“求导”这个运算求逆。
求出来的答案称为原函数。
那么有微积分基本定理 $\int_{a}^{b}f(x)dx = F(b) - F(a) $。其中 \(F\) 表示原函数。
泰勒级数(泰勒多项式)
比如说,我们有一个函数 \(f(1 - \cos \theta)\),对于 \(\theta\) 特别小的时候,答案是很难计算的,尤其是接近于 \(0\) 的时候。
这时候我们希望做出一个近似,比如 \(1 - \dfrac{\theta^2}{2}\) 来代替 \(\cos \theta\),你发现这两个函数在 \(x\) 接近 \(0\) 的时候非常精确!
但是,为什么呢?这个函数是哪里来的?
首先,假设我们已知要近似成一个二次函数 \(y=ax^2+bx+c\),并且希望近似出来的函数至少在 \(x=0\) 时和 \(\cos \theta\) 相等,那么代入可得 \(c=1\),然后还不够,我还希望在 \(0\) 处的导数也相等,否则稍稍偏移就会差之千里。那么可以得到 \(b = 0\),还不够!最好二阶导数也是一样的,又得到了 \(a = -0.5\)。
所以我们就得到了上文的式子。
尝试推广这个东西。
注意到我们就是在求一阶导数,二阶导数,三阶导数,……分别带入求出了一个多项式的值。
根据上文多项式求导的法则,实际上我们近似出来的函数应该长这样:
当只取一部分时,称为泰勒多项式,当取全体时,称为泰勒级数。
多项式好理解,那么级数呢?
你可以看作是一个无穷的数列求和,比如:
这种最后趋于一个确定值的情况,称为这个级数收敛,否则发散。
【尝试】推出 \(e^x\) 和 \(\ln(x)\) 的泰勒级数,并指出这是发散的还是收敛的。
至此,微积分入门就告一段落,但也记住:仅仅是入门。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号