不杂题不选做，weekday9

Day1

CF1083C Max Mex

换句话说就是找到一个最大的 \(i\) 使得 \(0,1,\dots,i\) 在一条链上，答案就是 \(i+1\)。

线段树维护 \([l,r]\) 是否在一条链上，如果是找出这条链。然后 \([l,mid]\) 和 \([mid+1,r]\) 的信息合并是不难的。最后在线段树上二分即可。
用单次查询复杂度 \(\mathcal O(1)\) 的 LCA，这样的时间复杂度是 \(\mathcal O(n\log n)\) 的。

CF1139E Maximize Mex

删数不好维护，考虑时光倒流变成加数。
单次答案如何计算？不难看出可以把潜力值 \(p_i\) 和社团 \(c_i\) 建出一个二分图，从小到大地去尝试匹配潜力值，第一个无法匹配的值就是 \(\operatorname{mex}\)。
把删数变成加数之后，\(\operatorname{mex}\) 是不减的，所以不需要每次都重新跑二分图匹配，而是可以在上一次结果的基础上继续匹配，时间复杂度 \(\mathcal O\!\left(n^2\right)\)。

CF285E Positions in Permutations

计数恰好转指定，就是指定有 \(k\) 个位置 \(i\) 满足 \(|P_i-i|=1\)，其余的任意。记原题中要求的值为 \(f_m\)，这里的值为 \(g_i\)，则在求出所有 \(g_i\) 后可以简单地二项式反演求出 \(f_m\)。
考虑 dp 求出 \(g_i\)。设 \(dp_{i,j,0/1,0/1}\) 表示在前 \(i\) 个位置中指定 \(j\) 个满足条件，剩下的先不填，\(i\) 是否被选，\(i+1\) 是否被选。这样最终的 \(g_i\) 实际上就是 \((dp_{n,i,0,0}+dp_{n,i,1,0})(n-i)!\)。
考虑转移。若 \(i\) 指定选 \(i-1\)，则

\[dp_{i,j,0,0}\gets dp_{i-1,j-1,0,0}\newline dp_{i,j,1,0}\gets dp_{i-1,j-1,0,1} \]

若 \(i\) 指定选 \(i+1\)（前提是 \(i\ne n\)），则

\[dp_{i,j,0,1}\gets dp_{i-1,j-1,0,0}+dp_{i-1,j-1,1,0}\newline dp_{i,j,1,1}\gets dp_{i-1,j-1,0,1}+dp_{i-1,j-1,1,1} \]

若 \(i\) 未被指定，则

\[dp_{i,j,0,0}\gets dp_{i-1,j,0,0}+dp_{i-1,j,1,0}\newline dp_{i,j,1,0}\gets dp_{i-1,j,0,1}+dp_{i-1,j,1,1} \]

初值为 \(dp_{1,0,0,0}=dp_{1,1,0,1}=1\)。

dp 直接做就行，时间复杂度 \(\mathcal O\!\left(n^2\right)\)。

CF1622F Quadratic Set

答案一定不小于 \(n-3\)。为啥？？
有式子：

\[\prod_{i=1}^{2k}i!=2^ki!\left[\prod_{i=1}^k(2i-1)!\right]^2 \]

• 当 \(n\equiv0\pmod 4\) 时只需要删去 \(\frac{n}{2}\) 即可。
• 当 \(n\equiv2\pmod 4\) 时需要删去 \(2\) 和 \(\frac{n}{2}\)。
• 当 \(n\equiv1\pmod 2\) 时删去 \(n\)，然后转为上面一个。

于是考虑挨个判断是否可行。对每个质数赋随机值，一个数的值是所有出现奇数次的质因子的异或值。这样一个阶乘的值可以递推得出。一个数对应的值是 \(0\) 说明它有极大概率是完全平方数。剩下的就很简单了。

Day2

P8820 [CSP-S 2022] 数据传输

\(k=1\) 是简单的。

\(k=2\) 可以知道最优路径一定只选择简单路径上的点，于是有转移方程：

\[f_i=\min(f_{i-1},f_{i-2})+v_i \]

写成 \((\min,+)\) 矩阵形式得到：

\[\begin{bmatrix}f_{i-1}&f_{i-2}\end{bmatrix}\times\begin{bmatrix}v_i&0\\v_i&\infty\end{bmatrix}=\begin{bmatrix}f_i&f_{i-1}\end{bmatrix} \]

可以预处理一个点到它的 \(2^k\) 级祖先的矩阵连乘积，然后询问时拼在一起。

\(k=3\) 时涉及到的点是毛毛虫。设 \(f_{i,j}\) 表示到一个在第 \(i\) 个点子树中，且离第 \(i\) 个点距离为 \(j\) 的点的最小代价，则有转移方程：

\[\begin{aligned}f_{i,0}&=\min(f_{i-1,0}+f_{i-1,1}+f_{i-1,2})+v_i\\f_{i,1}&=\min(f_{i-1,0},f_{i-1,1}+v_i')\\f_{i,2}&=f_{i-1,1}\end{aligned} \]

其中 \(v_i'\) 指所有第 \(i\) 个点的儿子 \(j\) 的 \(v_j\) 的最小值。
这同样可以用矩阵表示：

\[\begin{bmatrix}f_{i-1,0}&f_{i-1,1}&f_{i-1,2}\end{bmatrix}\times\begin{bmatrix}v_i&0&\infty\\v_i&v_i'&0\\v_i&\infty&\infty\end{bmatrix}=\begin{bmatrix}f_{i,0}&f_{i,1}&f_{i,2}\end{bmatrix} \]

每次询问时在 LCA 处将它的父亲也放进 \(v_{lca}'\) 就行。时间复杂度 \(\mathcal O\!\left((n+q)k^3\log n\right)\)。

CF494C Helping People

由于区间要么包含要么相离，可以建出一个森林。为了方便，增加一个 \(l=1,r=n,p=0\) 的操作，这样森林变成一棵树。
一个观察是操作后的最大值绝不会超过一开始的的最大值加 \(q\)。由于期望的定义，可以考虑对于每个可能达到的最大值求出达到它的概率，最后的计算就简单了。
设 \(f_{i,j}\) 表示区间 \([l_i,r_i]\) 中最大值不超过 \(j\) 的概率。则有

\[f_{i,j}=p_i\prod_kf_{k,j-1}+(1-p_i)\prod_kf_{k,j} \]

只有 \(j\in[\max([l_i,r_i]),\max([l_i,r_i])+q]\) 时需要计算。直接做就行。
处理区间 \(\max\) 用 ST 表。比较闲的话其实可以做到时间复杂度 \(\mathcal O\!\left(n+q^2\right)\)。

CF461E Appleman and a Game

st. 16:18 ed. 20:30

若给定一个串 \(s\)，如何求出其最小操作次数？由于子串的性质，若能取出一个更长的子串而不取是不优的，这是在给下一个要取出的子串徒增限制。于是可以每次删去一个最长的后缀满足其是一个子串，贪心地得到答案。

有性质：设使用不超过 \(l\) 个子串最多可以操作出所有长度为 \(n\) 的串，则一定可以操作出所有长度不超过 \(n\) 的串。于是可以二分答案 \(l\)。

考虑矩阵优化 dp。期望上一个子串加上一个字符不能再出现，因此设 \(f_{i,c}\) 表示最短的用 \(i\) 个 \(t\) 中子串不能表示出的以字符 \(c\) 开头的串长度，再设 \(g_{c,d}\) 为最短的以 \(c\) 开头，且在结尾加上一个字符 \(d\) 就不再是 \(t\) 中子串的 \(t\) 中子串的长度，那么有转移方程

\[f_{i,c}=\min_d(g_{c,d}+f_{i-1,d}) \]

其中 \(g_{c,d}\) 可以在 \(t\) 的 SAM 中预处理得出。至此，二分 \(l\) 后矩阵快速幂即可，也可以优化为倍增，倍增的时间复杂度为 \(\mathcal O\!\left(|\Sigma|^2|t|+|\Sigma|^3\log n\right)\)。

CF444E DZY Loves Planting

st. 20.32 ed. 21:39

求 \(\min\) 的 \(\max\) 想到二分，二分答案 \(ans\) 后把所有边权不小于 \(ans\) 的边断掉，序列 \(P\) 既合法又满足 \(f(P)\ge ans\) 就可以转述为 \(i,p_i\) 属于不同的连通块，且 \(p_i\) 最多选 \(x_{p_i}\) 次。
将这种选择建出二分图计算最大匹配，使用 Hall 定理可知记一个连通块内部点数为 \(a\)，外部 \(x_i\) 之和为 \(b\)，若 \(a>b\) 则不存在合法序列。
进一步可以发现 \(ans\) 不需要二分，可以在 \(ans\) 递增的过程中用并查集动态地合并连通块。如果比较闲的话时间复杂度可以达到 \(\mathcal O(n\alpha(n)+V)\)，其中 \(V\) 是边权的值域。

Day3

模拟赛T3 巡逻网络

先考虑 \(k=1\) 的情况。

原题中的 \(m+t\) 个点的曼哈顿距离之和可以拆成三部分：固定点间的贡献，可选点和固定点间的贡献，以及可选点间的贡献。第一个是定值，直接求出即可，第二个相当于是每个点有一个额外权值，记作 \(c_i\)。接下来处理第三个。
距离不预设大小是不好做的。若最终确定一些点 \(x_1,x_2,\dots,x_m\)，假定 \(x_1\le x_2\le\dots\le x_m\)，则曼哈顿距离之和为 \(\sum_{i=1}^m(2i-m-1)x_i\)。枚举顺序不太好，用状压预留位置然后一个个放进去是可以的。具体地，设 \(dp_{i,S}\) 表示考虑前 \(i\) 个位置，集合 \(S\) 已有数被填进去的贡献最大值。把 \(i\) 放进第 \(j\) 个位置时，它的贡献为 \((2j-m-1)x_i+c_i\)。这样的时间复杂度为 \(\mathcal O\!\left(nm2^m\right)\)。

当 \(k=2\) 时，类似地，设 \(dp_{i,S1,S2}\) 表示选中的点的 \(x\) 坐标占据 \(S1\) 集合，\(y\) 坐标占据 \(S2\) 集合的贡献最大值。由于有限制 \(|S1|=|S2|\)，合法的状态数只有
\(\displaystyle\sum_{i=0}^m\binom{m}{i}^2=\binom{2m}{m}\) 个，是 \(\displaystyle\mathcal O\!\left(\frac{4^m}{\sqrt m}\right)\) 级别的（可见 Wolfram|Alpha）。记实际状态数为 \(P\)，则时间复杂度为 \(\mathcal O\!\left(nm^2P\right)\)。

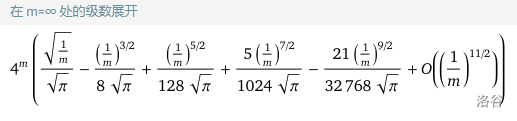
当 \(m=4,k=1\) 时，选出的四个点中间三段的系数分别为 \(3,4,3\)，所以这里可以直接设 \(dp_{i,j}\) 表示前 \(i\) 个数，选到第 \(j\) 段的贡献最大值。当 \(k=2\) 时再套一个上述的状压 dp 即可，此时时间复杂度变为 \(\mathcal O\!\left(nm^22^m\right)\)。