线段树总结

先搬一点热带运算的东西：

热带运算

热带运算（tropical arithmetic）是将加法 \(\oplus\) 定义为 \(\max\)（或 \(\min\)，此处仅讨论 \(\max\) 的部分），将乘法 \(\odot\) 定义为 \(+\) 的运算,在 \(\mathbb{\bar R}=\mathbb{R}\cup\{-\infty\}\) 上进行。
例子： \(2\oplus3=3\)，\(2\odot3=5\)，\(-\infty\oplus1=1\)，\(-\infty\odot1=-\infty\)，\(-\infty\oplus-\infty=-\infty\)。\(-\infty\odot-\infty\) 的值可以认为是未定义的，所以不在我们的讨论范围内。
由此我们可以发现 \(-\infty\oplus a=a\)，\(-\infty\odot a=-\infty(a\not=-\infty)\)，\(0\odot a=a\)。这是好的性质。它甚至有乘法分配律，即 \(a\odot(b\oplus c)=(a\odot b)\oplus(a\odot c)\)。
然而元素并没有加法逆元，如 \(a\oplus x=b(a>b)\) 无解。所以我们称三元组 \(\left(\mathbb{\bar R},\oplus,\odot\right)\) 是一个热带半环（tropical semiring）。
热带运算可以表示诸多线性规划题目中的方程组，热带矩阵乘法也可以类似地定义。

区间最值操作、区间历史最值

之前写线段树 3，一个节点内维护了 \(11\) 个值，其中有 \(4\) 个懒标记。
文章从另一种角度看待这些标记：矩阵。
线段树 3 中所有的操作都局限在 \(\max\) 和 \(+\) 这两种运算上，我们不如将矩阵乘法推广，变成一种类似热带矩阵的东西。然后这题就变成了：

维护矩阵序列 \(\left[\begin{matrix}a_i\\b_i\end{matrix}\right]\)，初始时 \(b_i=a_i\)，操作如下：

• \(\forall i\in[l,r],\left[\begin{matrix}a_i\\b_i\end{matrix}\right]\gets \left[\begin{matrix}k,-\infty\\-\infty,0\end{matrix}\right]\left[\begin{matrix}a_i\\b_i\end{matrix}\right]\)。
• 求 \(\sum_{i=l}^r\left[\begin{matrix}a_i\\b_i\end{matrix}\right]\)。
• 区间求和与区间取 \(\min\)。

每次操作之后，都有 \(\left[\begin{matrix}a_i\\b_i\end{matrix}\right]\gets \left[\begin{matrix}0,-\infty\\0,0\end{matrix}\right]\left[\begin{matrix}a_i\\b_i\end{matrix}\right]\)。

前面几个操作直接维护矩阵和和乘法标记矩阵，区间取 \(\min\) 可以同一般写法维护最大和非最大矩阵然后分类讨论，区间求和没有区别，也是维护最大值的个数 \(cnt\) 然后计算 \(sum\)。
但是如果直接记录整个矩阵不太好，我们可以考虑省去矩阵右侧的 \(-\infty\) 和 \(0\)，反正它们不变。

问题：上述做法已经将矩阵换成了热带矩阵，那如果在线段树 3 的基础上再加上区间乘一个数，还能做吗？

还有文章，介绍区间历史和。

线段树合并和分裂

合并：

int merge(int x,int y,int l,int r){
	if(!x||!y)return x+y;
	if(l==r){
		sum[x]+=sum[y];
		return x;
	}
	lc[x]=merge(lc[x],lc[y],l,mid);
	rc[x]=merge(rc[x],rc[y],mid+1,r);
	up(x);
	return x;
}

线段树分裂可以以一个值 \(k\) 对线段树分裂成前 \(k\) 小的数和其他数组成的两棵线段树。设左儿子有 \(l\) 个数，分类讨论：

• \(l<k\)：递归分裂右节点，左节点全部给第一棵。
• \(l=k\)：停止递归，左节点给第一棵，右节点给第二棵。
• \(l>k\)：与 \(l<k\) 类似。

时间复杂度 \(\mathcal O(\log n)\)。
然后就可以做模板了。

例题：排序
离线后二分加线段树判定是 \(\mathcal O(n\log^2n)\) 的，不够优，考虑 \(\mathcal O(n\log n)\) 做法。
可以使用一个 set，类似珂朵莉树去维护排序后的每个有序区间，遇到一个操作就先分裂再合并，然后标记升序还是降序。
这样做是很好的，因为它不仅在线，时间复杂度更优，还可以回答最后的整个序列。
所以合并两个有序序列可以使用权值线段树，做到均摊 \(\mathcal O(\log n)\)。
再维护一些东西应该可以区间排序区间求和，只要顺序不影响结果就行。区间最大子段和就不行。

李超线段树

之前在做最长双回文串时学的，后来才发现喜提最劣解......
它可以维护多条线段的单点极值。
使用 OIwiki 的一张图片：

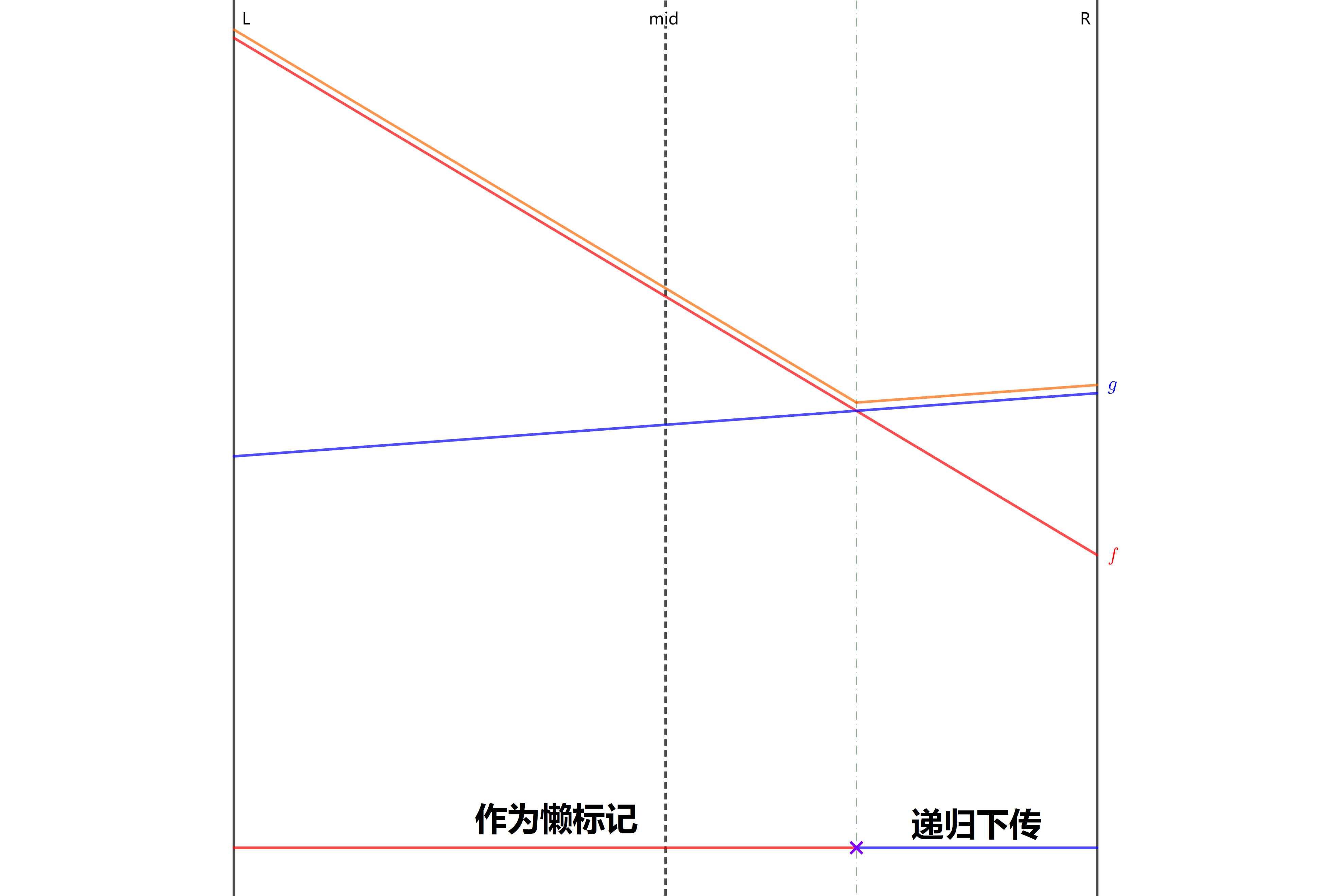
对于当前节点的标记和要更新的线段：如果要更新的线段在终点处值更大，就交换；接着看左右区间，如果有交点，递归更新。
标记并不一定是区间中在区间中点处取值最大的线段。
这样做修改中每次下传标记是 \(\mathcal O(\log n)\) 的，所以总体的时间复杂度是 \(\mathcal O(\log^2n)\) 的。
查询时不需要下传，直接标记永久化就行。复杂度 \(\mathcal O(\log n)\)。

回到最长双回文串。我们可以在跑 manacher 时顺便在两棵李超线段树上分别更新以 \(i\) 为左、右端点时的最长回文串，然后最后拼出双回文串即可。复杂度还是 \(\mathcal O(n\log^2 n)\) 的。
代码。

二维线段树

我之前写题时发明出四叉树，可以随随便便被卡掉......
二维线段树就是大线段树的节点是一棵棵小线段树。
有人说四叉树在对正方形做修改和查询操作时复杂度才是正确的？还是不如二维线段树。

无关的东西：Mokia
明面上是一个矩阵加矩阵求和，但是矩阵很大，矩阵中又有很多 \(0\)，不能用二维线段树。
但是如果看出它是一个三维偏序，这道题就做完了。