trie（字典树）总结

01 trie

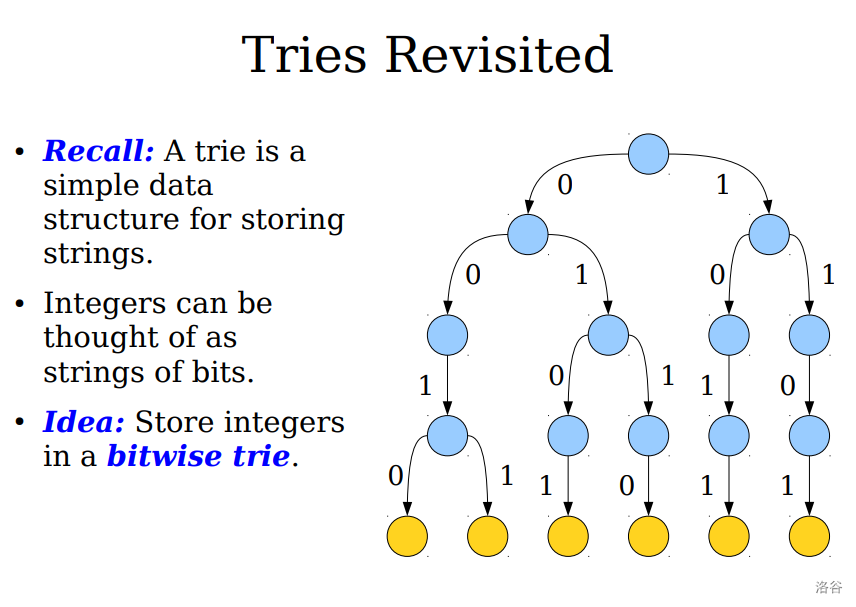
在 01 trie 中，若有 \(n\) 个数，每个数的二进制长度为 \(L\)，则空间复杂度为 \(\mathcal O(nL)\)，任何字典操作（存在性，插入删除，前驱后继，最大最小值）的时间复杂度都为 \(\mathcal O(L)\)。

但是才 \(L\)？我们有没有方法把所有字典操作都改进成 \(\mathcal O(\log L)\)，就像 vEB 树一样？答案是有的。

x-fast trie

一个想法是在字典树上二分。
可以对字典树的每一层建一个哈希表，每次询问一个节点的二进制前缀是否可以在一层中找到。
因为若一个节点可以找到，则他的祖先也都可以找到，反之则反，所以有单调性，可以二分。
现在询问一个值是否在 trie 中是 \(\mathcal O(1)\) 的，因为可以直接在哈希表中查询。但是查询前驱和后继还是 \(\mathcal O(L)\) 的，还能改进吗？
我们在找前驱时（后继类似），给定的值一定属于以下两种中的一种：

1. 在 trie 中（在叶子节点）
2. 不在 trie 中（在中间节点）

第一种的前驱一定是它左边的叶子节点。这提醒我们可以使用一些指针指向这些前驱后继。
我们可以把所有未使用的指针利用起来，0 指针指向前驱，1 指针指向后继（如果有的话）。
对于叶子节点，指针自然也不能浪费，可以指向它左边和右边的两个叶子节点。可以发现这类似一个双向链表。
再加上前面提到的 \(\mathcal O(L)\) 个哈希表，一棵 x-fast trie 就建出来了。

现在来看看 x-fast trie 的时间复杂度。
存在性是 \(\mathcal O(1)\) 的，前驱后继和最大最小（相当于 \(\infty\) 的前驱和 \(-\infty\) 的后继）都是 \(\mathcal O(\log L)\) 的。但是插入和删除较为暴力，只能均摊 \(\mathcal O(L)\) 解决（毕竟要增加、回收节点，更新指针等等）。

现在看来，只用 trie 肯定是不行的了，因为插入再怎么说 \(\mathcal O(L)\) 个节点是绝对要增加的。而且空间不是线性的，还是不够优。

y-fast trie

假设我们有一棵有 \(\mathcal\Theta(L)\) 个节点的平衡树，那么在上面执行的任何字典操作的时间复杂度自然都是 \(\mathcal O(\log L)\) 的。这给了我们一点希望。
基于此，我们还是使用一个 x-fast trie 来维护，只不过这次的节点是一棵棵大小为 \(\mathcal O(L)\) 的平衡树（红黑树等严格的最好）。
然而 trie 肯定是不能直接维护平衡树的，需要一个“代表元素”（representative）来间接维护。代表元素划定了树的边界。代表元素不一定要在平衡树中出现，但一定要比下一棵的最小值和代表元素小，且比上一棵的最大值和代表元素大（这样才有划分的功能）。

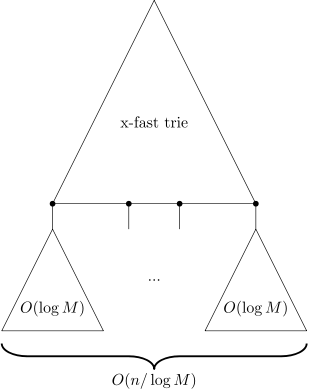
这样做，前驱后继、最大最小、存在性的时间复杂度没有变化。
对于插入，直接找到它的后继所在的平衡树然后插入，删除同理。
但平衡树的大小在不断改变，为了平衡，可以规定大小的上下界，比如 \([\frac{L}{2},2L]\)，在插入删除时分裂合并即可。可以证明这样做的均摊时间复杂度是 \(\mathcal O(\log L)\) 的。
同时看空间，可以发现是 \(\mathcal O(n)\) 的。这样就做到了对标 vEB 树。

可持久化？你是强者。
有没有 z-fast trie？有是有的。

可持久化 01 trie

实在迫不得已要用这个的时候，一般都和什么神秘位运算有关系，比如“区间最大双值异或和”。
比如这道，这道，还有这道都是这样的。
实现没什么好说的，一般情况下就是一边继承一边递归，维护一个区间数的个数，数的结尾。

题：[THUSC2015] 异或运算

后缀树

直接用 trie 做后缀树，空间直逼 \(\mathcal O(n^2)\)，需要手法维护。
可以发现其实很多点都是用处不大的，我们不妨让 trie 上的一条边可以存储多个字符，整体就被压缩了。这样压缩之后的结构，节点个数最多为 \(2n\) 个。
有 Ukkonen 算法，可以在后面添加字符的同时实时计算后缀树。
但是此时就和 trie 关系不大了，所以先咕。