P5176 公约数

题意：求

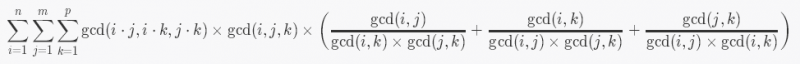
对 \(10^9+7\) 取模的值。

这东西一看就十分炸裂，如何化简？
首先有恒等式：

\[\gcd(ij,ik,jk)=\frac{\gcd(i,j)\gcd(i,k)\gcd(j,k)}{\gcd(i,j,k)} \]

它可以通过唯一分解定理证明。
然后很多东西都可以约分了，最后式子化为：

\[\sum_{i=1}^n\sum_{j=1}^m\sum_{k=1}^p\left[\gcd(i,j)^2+\gcd(i,k)^2+\gcd(j,k)^2\right] \]

接下来把它分成三个结构一样的和式，如下：

\[\sum_{i=1}^n\sum_{j=1}^m\sum_{k=1}^p\gcd(i,j)^2+\sum_{i=1}^n\sum_{j=1}^m\sum_{k=1}^p\gcd(i,k)^2+\sum_{i=1}^n\sum_{j=1}^m\sum_{k=1}^p\gcd(j,k)^2 \]

现在我们来看第一个和式。可以发现 \(p\) 仅作贡献次数的作用，所以把它提到前面：

\[p\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)^2 \]

仅看 \(p\) 后面那个式子，不妨设 \(n\le m\)，然后枚举因数：

\[\sum_{k=1}^{n}k^2\sum_{i=1}^{\left\lfloor\frac{n}{k}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac{m}{k}\right\rfloor}[\gcd(i,j)=1] \]

将 \([x=1]\) 转化为 \(\underset{d|x}{\sum}\mu(d)\)，有：

\[\sum_{k=1}^{n}k^2\sum_{i=1}^{\left\lfloor\frac{n}{k}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac{m}{k}\right\rfloor}\sum_{d|i,d|j}\mu(d) \]

\[\sum_{k=1}^{n}k^2\sum_{d=1}^{\left\lfloor\frac{n}{k}\right\rfloor}\sum_{i=1}^{\left\lfloor\frac{n}{dk}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac{m}{dk}\right\rfloor}\mu(d) \]

此处 \(i,j\) 和上文中 \(p\) 的意义一致，可以类似转化：

\[\sum_{k=1}^{n}k^2\sum_{d=1}^{\left\lfloor\frac{n}{k}\right\rfloor}\left\lfloor\frac{n}{dk}\right\rfloor\left\lfloor\frac{m}{dk}\right\rfloor\mu(d) \]

令 \(T=dk\)，则有：

\[\sum_{T=1}^{n}\left(\left\lfloor\frac{n}{T}\right\rfloor\left\lfloor\frac{m}{T}\right\rfloor\sum_{d|T}d^2\mu\left(\frac{T}{d}\right)\right) \]

设 \(f(n)=\underset{d|n}{\sum}d^2\mu\left(\frac{n}{d}\right)\)，则上式可写作：

\[\sum_{T=1}^{n}\left\lfloor\frac{n}{T}\right\rfloor\left\lfloor\frac{m}{T}\right\rfloor f(T) \]

可以发现这就是一个整除分块的形式，如果可以计算出 \(f(n)\) 的前缀和，就可以以 \(\mathcal O(\sqrt{n})\) 的时间复杂度内解决单次询问。所以问题转化到了如何快速求出 \(f(n)\)。
可以直观看出 \(f=g*\mu\)，其中 \(g(n)=n^2\)。这告诉我们它是一个积性函数，提示着我们可以像线性筛一样把它递推计算出来。
线性筛中要考虑到的四条性质，此处一一列举：

• \(f(1)=1\)。
• \(f(p)=p^2-1\)，其中 \(p\) 是质数。
• \(f(xy)=f(x)f(y)\)，其中 \(x\perp y\)。
• \(f(px)=p^2f(x)\)，其中 \(p\) 是 \(x\) 的最小质因子。

此处写一下第四条的证明：

\[f\left(p^k\right)=\underset{d|p^k}{\sum}d^2\mu\left(\frac{p^k}{d}\right) \]

其中 \(p\) 是质数，\(k\) 是任意大于等于二的整数。可知 \(d=p^l\)，其中 \(0\le l\le k\)。由于 \(\mu\) 的定义，这个和式中真正有贡献的仅有两项：

\[\begin{aligned}f\left(p^k\right)&=p^{2k}\mu(1)+p^{2k-2}\mu(p)\\&=p^{2k}-p^{2k-2}\\&=(p^2-1)p^{2k-1}\\&=f(p)p^{2k-1}\end{aligned} \]

观察可知 \(f\left(p^k\right)=p^2f\left(p^{k-1}\right)\)，在推广一下即可得出第四条。
最后设上面那个式子为 \(h(n,m)\)，则本题答案为：

\[ph(n,m)+mh(n,p)+nh(m,p) \]

然后这道题就做完了。代码：

#include<bits/stdc++.h>
using namespace std;

const int N=2e7+5,P=1e9+7;
typedef long long ll;

int p[N/7],pind;
bool nonp[N];
int f[N];
void ini(int n=2e7){
	nonp[1]=true,f[1]=1;
	for(int i=2;i<=n;i++){
		if(!nonp[i])p[++pind]=i,f[i]=((ll)i*i-1)%P;
		for(int j=1;j<=pind&&i*p[j]<=n;j++){
			nonp[i*p[j]]=true;
			if(!(i%p[j])){
				f[i*p[j]]=(ll)f[i]*p[j]%P*p[j]%P;
				break;
			}
			f[i*p[j]]=(ll)f[i]*f[p[j]]%P;
		}
	}
	for(int i=1;i<=n;i++){
		f[i]+=f[i-1];
		if(f[i]>=P)f[i]-=P;
	}
}

int calc(int n,int m){
	int ans=0;
	if(n>m)swap(n,m);
	for(int l=1,r;l<=n;l=r+1){
		r=min(n/(n/l),m/(m/l));
		ans=(ans+(ll)(n/l)*(m/l)%P*(f[r]-f[l-1])%P)%P;
	}
	return ans;
}

int main(){
	
	ios::sync_with_stdio(0),cin.tie(0);
	ini();
	int t;cin>>t;
	while(t--){
		int n,m,p;cin>>n>>m>>p;
		int ans=((ll)p*calc(n,m)%P+(ll)n*calc(m,p)%P+(ll)m*calc(n,p)%P)%P;
		cout<<(ans+P)%P<<"\n";
	}
	
	return 0;
}