寒假集训——基础数论6 线性代数，行列式

目录

• 矩阵
  • 定义
  • 性质
    • 特殊矩阵
    • 运算
  • 矩阵加速
    • P1255 数楼梯
    • P3390 【模板】矩阵快速幂
• 高斯消元法
  • P3389 【模板】高斯消元法
  • 解的判断
  • 矩阵求逆
• 行列式
  • 概念
  • 性质
  • 矩阵树定理
• prufer序列
  • 构造方法
  • 例题
• 线性相关，线性无关
• 线性极大无关组
• 线性基

矩阵

定义

简单来说矩阵就是一个 \(n\) 行 \(r\) 列的阵，实在不行可以理解成一个二维数组

\[ %开始数学环境 \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,r}\\ a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,r}\\ \cdots \\ a_{n,1} & a_{n,2} & a_{n,3} & \cdots & a_{n,r}\\ \end{array} \right] %右括号 \]

这就是一个矩阵。
$ n = r $ 的矩阵也可以叫方阵

性质

特殊矩阵

自然的，就像 \(0\) 在实数中有重要的地位，自然也有一些矩阵是需要单独记忆的。

1. 单位矩阵
   主对角线上的元素皆为1，其他元素均为0的矩阵，记为 \(I\) 。

\[ \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] %右括号 \]

这就是一个 $ 3 * 3 $ 的单位矩阵。
2.对称矩阵
所有主对角线右上方的元素和主对角线左下方的元素对应相等的矩阵。即 $ a_{i,j} = a_{j,i} $ 。

\[ \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 6 \\ \end{array} \right] %右括号 \]

这个就算是一个对称矩阵

运算

显然的矩阵肯定是可以运算的，所以我们定义：

• 矩阵同型且对应元素相等，则矩阵相等
• 矩阵加法:在两个相同大小的矩阵。两个 $ m*n $ 矩阵 \(A\) 和 \(B\) 的和，标记为 \(A+B\) ，一样是个 \(m*n\) 矩阵，其内的各元素为其相对应元素相加后的值。
• 也可以做矩阵的减法，只要其大小相同的话。 \(A-B\) 内的各元素为其相对应元素相减后的值，且此矩阵会和 \(A,B\) 有相同大小。

\[\left[ \begin{array}{ccc} 1 & 1 & 5\\ 1 & 4 & 1 \\ 9 & 1 & 9 \\ \end{array} \right] = \left[ \begin{array}{ccc} 1 & 1 & 5\\ 1 & 4 & 1 \\ 9 & 1 & 9 \\ \end{array} \right] \]

\[\left[ \begin{array}{ccc} 1 & 1 & 4\\ 5 & 1 & 4 \\ 1 & 1 & 4 \\ \end{array} \right] + \left[ \begin{array}{ccc} 1 & 9 & 1\\ 9 & 8 & 1 \\ 0 & 1 & 9 \\ \end{array} \right] = \left[ \begin{array}{ccc} 2 & 10 & 5\\ 14 & 9 & 5\\ 1 & 2 & 13 \\ \end{array} \right] \]

\[\left[ \begin{array}{ccc} 1 & 1 & 4\\ 5 & 1 & 4 \\ 1 & 1 & 4 \\ \end{array} \right] - \left[ \begin{array}{ccc} 1 & 9 & 1\\ 9 & 8 & 1 \\ 0 & 1 & 9 \\ \end{array} \right] = \left[ \begin{array}{ccc} 0 & -8 & 3\\ -4 & -7 & 3\\ 1 & 0 & -5 \\ \end{array} \right] \]

比较有趣的是矩阵的乘法 ，
\(A\) 为 \(m * p\) 的矩阵，\(B\) 为 \(p*n\) 的矩阵，那么称 \(n * m\) 的矩阵 $C $为矩阵 \(A\) 与 \(B\) 的乘积，记作 ，其中矩阵 \(C\) 中的第 \(i\) 行第 \(j\) 列元素可以表示为

\[c_{i,j} = \sum^{r}_{k = 1} a_{i,k} * b_{k,j} \]

举个例子

\[A = \left[ \begin{array}{cc} 1 & 1 & 4\\ 5 & 1 & 4 \\ \end{array} \right] \]

\[B = \left[ \begin{array}{ccc} 9 & 1 & \\ 8 & 1 \\ 1 & 9 \\ \end{array} \right] \]

则

\[C = AB = \left[ \begin{array}{ccc} 1 * 9 + 5 * 1 & 1 * 9 + 5 * 1 & 1 * 9 + 5 * 1\\ 1 * 8 + 1 * 1 & 1 * 8 + 1 * 1 & 1 * 8 + 1 * 1\\ 4 * 1 + 4 * 9 & 4 * 1 + 4 * 9 & 4 * 1 + 4 * 9\\ \end{array} \right] \]

看起来是不是挺抽象的，但是我们具体的来看
对于第一行第一列值来说，相当于 \(B\) 的第一列
与\(A\) 的第一列 相乘相加

\[\left[ \begin{array}{ccc} 1 & 5\\ \end{array} \right] * \left[ \begin{array}{c} 9 & 1 \\ \end{array} \right] = \left[ \begin{array}{ccc} 1 * 9 + 5 * 1 \\ \end{array} \right] \]

大概就是这种感觉

• 乘法结合律： $ (AB)C=A(BC)． $
• 乘法左分配律： $(A+B)C=AC+BC $
• 乘法右分配律： $C(A+B)=CA+CB $
• 需要注意的是，矩阵乘法并不满足交换律，即

\[AB \neq BA \]

矩阵加速

讲了这么久矩阵，现在我们来看看矩阵到底可以干什么

P1255 数楼梯

首先，我们可以几乎完全不用动脑的写出一个最简单的dp

#include <bits/stdc++.h>
#define for1(i,a,b) for(int i = a;i <= b ;i ++)
#define ll long long
using namespace std;
const int maxn = 5005 + 5;
int n,dp[maxn];

int main() 
{
    cin >> n;
    dp[1] = 1;
    dp[2] = 2;
    for1(i,3,n)
    	dp[i] = dp[i - 1] + dp[i - 2];
	cout<< dp[n]; 
    return 0;
}

但是现在我说，不够快，再快一点。
此时我们就可以使用矩阵来给他加速了
我们注意看这个方程

dp[i] = dp[i - 1] + dp[i - 2];

假如我把这三个参数丢进矩阵里面去

\[\left[ \begin{array}{ccc} dp[i] & dp[i - 1] & dp[i - 2]\\ \end{array} \right] \]

假如我们让这个矩阵乘上一个另一个矩阵，使它变成

\[\left[ \begin{array}{ccc} dp[i + 1] & dp[i] & dp[i - 1]\\ \end{array} \right] \]

我们通过矩阵乘法的定义去构造一个这样的矩阵不就🆗了
我们肯定希望乘上构造矩阵以后变成这样

\[\left[ \begin{array}{ccc} dp[i] * 1 + dp[i - 1] * 1 + dp[i - 2] * 0 & dp[i] * 1 + dp[i - 1] * 0 + dp[i - 2] * 0 & dp[i] * 0 + dp[i - 1] * 1 + dp[i -2] * 0\\ \end{array} \right] \]

此时，我们就可以很显然的构造出矩阵了

\[\left[ \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1\\ 0 & 0 & 0\\ \end{array} \right] \]

我们再仔细观察一下，会发现 \(dp[i + 1] = dp[i] + dp[i - 1]\) , $dp[i - 1] $ 似乎卵用没有，所以我们把它拿走。

\[\left[ \begin{array}{ccc} dp[i] & dp[i - 1]\\ \end{array} \right] \]

此时构造矩阵就变成了

\[\left[ \begin{array}{ccc} 1 & 1\\ 1 & 0\\ \end{array} \right] \]

又可以做一个优化。

我们想求 \(dp[n]\) 时，只需要拿初始矩阵不停的乘构造矩阵就可以了。
但是如果我们就这样乘 \(n\) 次的话，和之前复杂度并没有什么区别。
此时就需要引入

P3390 【模板】矩阵快速幂

实际上我们拿 \(struct\) 封装起来，再自定义乘法运算 这个就变成了普通的快速幂。

#include<bits/stdc++.h>
#define for1(i,a,b) for(int i = a;i<=b;i++)
#define ll long long
#define mp(a,b) make_pair(a,b)
using namespace std;
const long long mod=1000000007;
struct node {
	long long a[101][101];
} A,ans;
long long n;
node operator*(const node &x,const node &y) {
	node a;
	for1(i,1,n)
		for1(j,1,n)
			a.a[i][j]=0;
	for1(i,1,n)
		for1(j,1,n)
			for1(k,1,n) {
				a.a[i][j]+=x.a[i][k]*y.a[k][j]%mod;
				a.a[i][j]%=mod;
			}
	return a;
}
int main()
{
	long long k;
    cin>>n>>k;
	for1(i,1,n)
		for1(j,1,n)
			cin>>A.a[i][j];
	for1(i,1,n)
		ans.a[i][i]=1;
	while(k>0)
	 {
		if(k%2==1) ans=ans*A;
		A=A*A;
		k=k>>1;
	}
	for1(i,1,n)
	{
		for1(j,1,n)
			cout<<ans.a[i][j]<<' ';
		cout<<endl;
	}
	return 0;
}

掌握了快速幂之后，我们的就可以将dp的复杂度从 \(O(n)\) 降到 \(O(\log n)\) 了。

高斯消元法

就是一堆这样的方程，我们要求出所有的 \(x\) 的值。

\[\left\{ \begin{array}{c} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1 \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2 \\ \cdots \\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \end{array} \right. \]

我们来光看简介是不是觉得非常难，但是我们思考初中是是怎么解二元一次方程的，比如

\[\left\{ \begin{array}{c} 3x_1 + 2x_2 = 13 (1) \\ 2x_1+3x_2= 17 (2)\\ \end{array} \right. \]

我们是不是用 $ (1) * \frac{3}{2} - (2) $ ,算出 \(x_2\) 的值，再带回去算出 \(x_1\) ?
是的，这就是高斯消元法，只是我们要推广到 \(n\) 元一次方程。

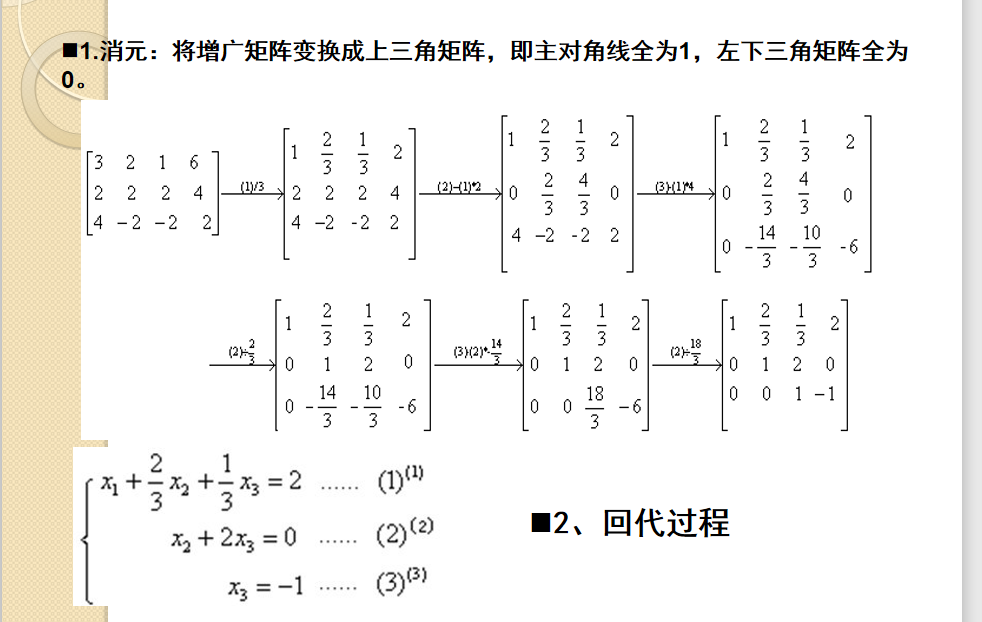
P3389 【模板】高斯消元法

看起来简单，但实际上打起来代码细节很多，所以其实是一道蓝题

#include<bits/stdc++.h>
#define for1(i,a,b) for(register int i=a;i<=b;i++)
#define ll long long
#define debug(a,b) printf("%s Now is %d\n",a.c_str(),b);
using namespace std;
double a[105][105];
int n;
int main()
{
	scanf("%d",&n);
	for1(i,1,n)
		for1(j,1,n+1)
			scanf("%lf",&a[i][j]);
	for1(i,1,n)
	{
		int max=i;
		for1(j,i+1,n)
			if(fabs(a[j][i])>fabs(a[max][i]))
				max=j;
		for1(j,1,n+1)
			swap(a[i][j],a[max][j]);
		if(a[i][i]==0)
		{
			puts("No Solution");
			return 0;
		}
		for1(j,1,n)
			if(j!=i)
			{
				double ji=a[j][i]/a[i][i];
				for1(k,i+1,n+1)
					a[j][k]-=a[i][k]*ji;
			}
	}
	for1(i,1,n)
		if(a[i][n+1]/a[i][i]==0) 
		{
			puts("No Solution");
			return 0;
		}
	for1(i,1,n)
		printf("%.2lf\n",a[i][n+1]/a[i][i]);
		
	return 0;
}

解的判断

我们不难想到，对于任意一个线性方程组，其实有无穷多解，唯一解，无解三种情况，那么我们判断就需要引入一个新的概念

我在网上查了一大堆定义，又是什么行列式，又是什么 \(n\) 维向量的，就挑一种最简单的来看。
简单来说，我们用高斯消元把一个矩阵化成一个上三角矩阵之后，它的非 \(0\) 行数之和就是矩阵的秩.
实在不懂就看这个：https://zhuanlan.zhihu.com/p/108093909

关键在于增广矩阵[A B]化成阶梯非零行的行数与系数矩阵A化成阶梯形矩阵后非零行的行数是否相等。因此，线性方程组是否有解，就可以用其系数矩阵和增广矩阵的秩来描述。
【定理】线性方程组有解的充分必要是 $ r(A)=r(A B)$ 。
推论1：线性方程组有唯一解的充分必要条件是 $r(A)＝r(A B)=n $ 。
推论2：线性方程组有无穷多解的充分必要条件是 \(r(A)＝r(A B)<n\) 。
推论3：线性方程组无解的充分必要条件是 \(r(A)<r(A B)\) 。

比如

\[A = \left[ \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 0 & 1\\ 0 & 0 & 0\\ \end{array} \right] \]

\[r(A) = 2 \]

\[B = \left[ \begin{array}{ccc} 2 \\ 2\\ 0\\ \end{array} \right] \]

\[(A,B) = \left[ \begin{array}{ccc} 1 & 1 & 0 & | & 2\\ 0 & 0 & 1 & | & 2\\ 0 & 0 & 0 & | & 0\\ \end{array} \right] \]

\[r(A B) = 2 \]

此时 $ r(A)＝r(A B)<n $ 是无穷解

---

\[A = \left[ \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 0 & 1\\ 0 & 0 & 0\\ \end{array} \right] \]

\[r(A) = 2 \]

\[B = \left[ \begin{array}{ccc} 2 \\ 2\\ 1\\ \end{array} \right] \]

\[(A,B) = \left[ \begin{array}{ccc} 1 & 1 & 0 & | & 2\\ 0 & 0 & 1 & | & 2\\ 0 & 0 & 0 & | & 1\\ \end{array} \right] \]

\[r(A B) = 3 \]

此时 $ r(A) < r(A B) $ 是无解

---

\[A = \left[ \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0\\ 1 & 0 & 0\\ \end{array} \right] \]

\[r(A) = 3 \]

\[B = \left[ \begin{array}{ccc} 2 \\ 1\\ 1\\ \end{array} \right] \]

\[(A,B) = \left[ \begin{array}{ccc} 1 & 1 & 0 & | & 2\\ 0 & 1 & 0 & | & 1\\ 0 & 0 & 1 & | & 1\\ \end{array} \right] \]

\[r(A B) = 3 \]

此时 $ r(A) = r(A B) = n $ 有唯一解

矩阵求逆

P4783 【模板】矩阵求逆

#include<bits/stdc++.h>
#define for1(i,a,b) for(register int i = a;i <= b; i++)
#define ll long long
using namespace std;

const int maxn = 405;
const ll mod = 1e9+7;
int n;
ll a[maxn][maxn * 2 +1 ];
ll ksm(ll x,ll k)
{
	ll res = 1;
	while(k)
	{
		if(k % 2 == 1) res = res* x %mod;
		x = x * x%mod;
		k >>= 1;
	}
	return res%mod;
}
int main()
{
	cin >> n;
	for1(i,1,n)
		for1(j,1,n)
			cin >> a[i][j],a[i][i + n] = 1;
	
		for1(i,1,n)
		{
			int mx = i;
			for1(j,i + 1,n)
				if(a[j][i] > a[mx][i]) 
					mx = j;
			if(mx != i) 
				swap(a[i],a[mx]);
			if(!a[i][i])
			{
				puts("No Solution");
				return 0;
			}
		
		ll ji = ksm(a[i][i],mod-2);	
		for1(k,1,n)
		{
			if(k==i) continue;
			ll fz = a[k][i] * ji %mod;
			for1(j,i,n * 2)
				a[k][j] = ((a[k][j] - fz * a[i][j]) % mod+mod) % mod;
		} 
		
		for1(j,1,n * 2) 
			a[i][j] = a[i][j] * ji % mod;
	
	}	
	
	for1(i,1,n)
	{
		for1(j,n + 1, n + n)
			cout << a[i][j] << ' ';
		cout<<'\n';
	}
    return 0;
}

行列式

概念

网上查到的定义基本都是这样的，实在是过于炫酷了，完全看不懂，所以建议直接记形似这种的东西都叫行列式就对了,同时这玩意是可以算出一个具体的数字的。

\[\left | \begin{matrix} a_{1,1} & a_{1,2} & a_{1,3} & ... & a_{1,m} \\ a_{2,1} & a_{2,2} & a_{2,3} & ... & a_{2,m} \\ ... \\ a_{n,1} & a_{n,2} & a_{n,3} & ... & a_{n,m}\\ \end{matrix} \right | \]

性质

行列式的计算是非常抽象的，首先我们先看三阶及以下的计算方法。

一阶行列式就是它本身。

二三阶行列式计算方法：

值得一提的是，我们平时做解析几何的时候计算的法向量也是使用这玩意算的。

而n阶矩阵的计算方法之一是将其使用高斯消元变成上三角矩阵，并且记录下行列式变化的系数，然后将对角线乘起来的积再乘上系数就可以了。

矩阵树定理

非常优雅且神奇的定理。

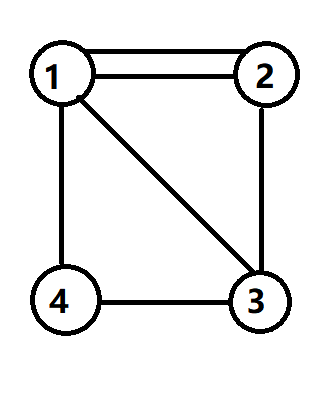
对于这样的一张图，我们会发出疑问：对于任意一张图，如何求它的生成树个数？
假设这个为图 \(G\) , 它的邻接矩阵为 \(A\) , 度数矩阵为 \(D\)
(是允许有重边的，度数矩阵就是第 \(i\) 行第 \(i\) 列是编号为 \(i\) 的点的度数，重边也算，其他为 \(0\) )

\[A = \left[ \begin{array}{ccc} 0 & 2 & 1 & 1\\ 2 & 0 & 1 & 0\\ 1 & 1 & 0 & 1\\ 1 & 0 & 1 & 0\\ \end{array} \right] , D = \left[ \begin{array}{ccc} 4 & 0 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 2\\ \end{array} \right] \]

我们定义一张图的 \(Kirchhoff\) 矩阵

\[K = D - A \]

\[K = \left[ \begin{array}{ccc} 4 & -2 & -1 & -1\\ -2 & 3 & -1 & 0\\ -1 & -1 & 3 & -1\\ -1 & 0 & -1 & 2\\ \end{array} \right] \]

• 1.Kirchhoff矩阵同时去掉任意一行一列，剩下的矩阵行列式绝对值相等.

• 2.Kirchhoff矩阵同时去掉任意一行一列，剩下的矩阵的行列式绝对值，就是这个无向图的生成树个数.

我们试一试

\[\left[ \begin{array}{ccc} 3 & -1 & 0\\ -1 & 3 & -1\\ 0 & -1 & 2\\ \end{array} \right] = \left[ \begin{array}{ccc} 3 & -1 & 0\\ -1 & 3 & -1\\ 0 & -1 & 2\\ \end{array} \right] \begin{array}{ccc} 3 & -1\\ -1 & 3\\ 0 & -1 \\ \end{array} = 3 * 3 * 2 + 0 + 0 - 0 - 3 - 2 = 13 \]

(一个特例:完全图的生成树个数是 \(n^{n-2}\) )

prufer序列

构造方法

对于一棵无向树，删除其中最小的叶子节点，将其相连的点的标号加入集合


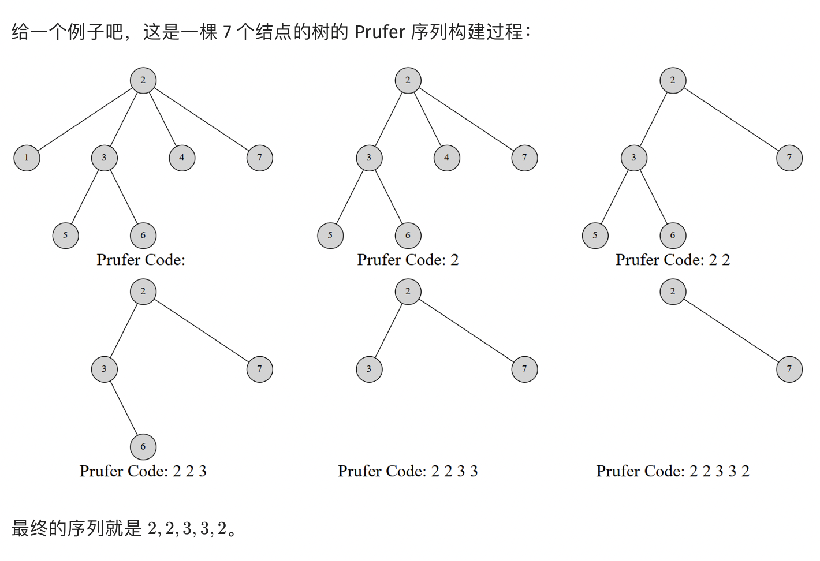
由Prufer序列构造的过程，我们可以发现其具有两个显而易见的性质。

• 构造完后剩下的两个节点里，一定有一个是编号最大的节点。

• 对于一个 度的节点，其必定在序列中出现 次，因为每次删去其子节点它都会出现一次，最后一次则是删除其本身。一次都未出现的是原树的叶子节点。

例题

P6086 【模板】Prufer 序列
还有个序列转树的，本质上没有区别

#include<bits/stdc++.h>
#define for1(i,a,b) for(register ll i = a;i <= b; i++)
#define ll long long
using namespace std;
const int maxn = 6e6 + 5;
const int mod = 1e9 + 7;
ll n, ji, f[maxn], p[maxn], d[maxn];
ll ans;

void cl1() 
{
	for1(i,1,n - 1)
		cin >> f[i],
		++d[f[i]];
		
	for (int i = 1, pos = 1; i <= n - 2; i++, pos++) 
	{
		while (d[pos] != 0)
		    pos++;
		p[i] = f[pos];
		while (i <= n - 2 && !--d[p[i]] && p[i] < pos) 
			p[i+1] = f[p[i]], 
			i ++;
	}
	for1(i,1,n - 2) 
		ans ^= 1ll * i * p[i];
}

void cl2() 
{
	for1(i,1,n - 2)
		cin >> p[i], 
		d[p[i]] ++ ;
		
	 p[n - 1] = n;
	 
	for (int i = 1, pos = 1; i < n; i++, pos++) 
	{
		while (d[pos] != 0) 
			pos++; 
		f[pos] = p[i];
		while (i < n && !--d[p[i]] && p[i] < pos) 
			f[p[i]] = p[i+1],
			i ++;
	}
	for1(i,1,n - 1)
		ans ^= i * f[i];
}


int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> n >> ji;
	
	if(ji == 1)
		cl1();
	else 
		cl2();
	cout << ans << '\n';
	
    return 0;
}

用处以后用到再写

线性相关，线性无关

找了几个通俗的例子

线性极大无关组

暂时也没搞懂到底是什么，反正考到了也暂时不会写，先放着。

线性基

P3812 【模板】线性基
太抽象了，建议直接记住在考试的时候可以拿来干嘛就得了

• 快速查询一个数是否可以被一堆数异或出来
• 快速查询一堆数可以异或出来的最大/最小值
• 快速查询一堆数可以异或出来的第k大值
  题解：https://www.luogu.com.cn/blog/szxkk/solution-p3813

#include <bits/stdc++.h>
#define for1(i,a,b) for(register ll i = a;i <= b;i ++)
#define ll long long
using namespace std;
const ll maxn = 2020;
const ll mod = 1e9 + 7;
int n, m;
struct node{
	ll p[64];
	ll d[64];
	ll cnt;
	node()
	{
		memset(p,0,sizeof(p));
		cnt = 0;
	}
	
	void Rebuild()
	{
		cnt = 0;
		for(ll i = 63;i >= 0 ;i --)
			for(int j = i - 1;j >= 0;j --)
				if(p[i] & (1ll << j))
					p[i] ^= p[j];
					
		for1(i,0,63)
			if(p[i])
				d[cnt ++] = p[i]; 
		
	}
	
	ll Kth(ll k)//求能表示出来的第k大
	{
		if(k >= (1ll << cnt))
			return -1; 
		ll ans = 0;
		for(ll i = 63;i >= 0;i--)
			if(k & (1ll << i))
				ans ^= p[i];
		return ans;
	} 
	
	void Insert(ll x)
	{
		for(ll i = 63;i >= 0;i--)
			if(x & (1ll << i)) 
			{
				if(!p[i])
				{
					p[i] = x;
					cnt ++;
					break;	
				}
				else
					x ^= p[i];
			}
		return ;
	}
	
	ll FindMax()
	{
		ll ans = 0;
		for(ll i = 63;i >= 0;i--)
		{
			if((ans ^ p[i]) > ans) 
			{
				ans ^= p[i];
			}
		}
		return ans;
	}
}xian;
int main() 
{
//	ios::sync_with_stdio(false);
//	cin.tie(nullptr);
	cin >> n;
	ll x;
	for1(i,1,n)
		cin >> x , xian.Insert(x);
	cout << xian.FindMax() << '\n';
    return 0;
}