寒假集训——基础数论4 多项式 FFT 生成函数

多项式

定义

用人话来说，就是一个函数

\[f(x) = a_1x^n + a_2x^{n - 1} + ... + a_nx^{1} +a_{n + 1} x^0 \]

这就是一个n次多项式
举个例子

\[f(x) = 3x^2 + 2x + 1 \]

这就是一个二次多项式

卷积

卷积官方给出的定义似乎是这样的：（冷知识，百度百科甚至没有卷积这个词条）
卷积是一种通过两个函数 $ 𝑓 $ 和 $ 𝑔 $ 生成第三个函数的一种数学算子

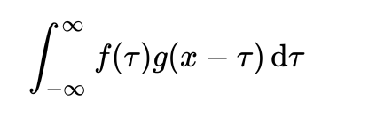
这个我也没看懂是什么意思
简单来说，就是

\[f(x) = a_1x^n + a_2x^{n - 1} + ... + a_nx^{1} +a_{n + 1} x^0 \]

\[g(x) = b_1x^n + b_2x^{n - 1} + ... + b_nx^{1} +b_{n + 1} x^0 \]

\[h(x) = f(x) * g(x) = c_1x^n + c_2x^{n - 1} + ... + c_nx^{1} +c_{n + 1} x^0 \]

$h(x)$ 就是 $f(x)$ 与 $g(x)$ 的卷积。
举个例子：

\[f(x) = 2x + 1 \]

\[g(x) = x - 2 \]

\[h(x) = f(x) * g(x) = (2x + 1)(x - 2) \]

\[= 2x^2 -3x - 2 \]

点值表示法

首先我们思考初一学到的一个真理：

到了初三，我们有知道了同一平面三个点可以确定一个二次函数，
自然的，我们会情不自禁的想

事实上的确如此，一个 $n$ 次多项式是可以被 $n + 1$ 点给确定下来的，也就是说

\[f(x) = \{ (x_0,f(x_0)),(x_1,f(x_1))...(x_{n},f(x_{n})) \} \]

\[g(x) = \{ (x_0,g(x_0)),(x_1,g(x_1))...(x_{n},g(x_{n})) \} \]

而此时，$f(x)$ 与 $g(x)$ 的卷积就是

\[h(x) = \{ (x_0,g(x_0)f(x_0)),(x_1,g(x_1)f(x_1))...(x_{n},g(x_{n})f(x_n)) \} \]

FFT

定义

既然介绍了卷积，那我们就应该思考，卷积怎么求最快，此时就引入大名鼎鼎的FFT，

这玩意看着很nb，说起来也很nb（在同学们面前大声地讨论，而且还不能叫FFT，要叫快速傅里叶变换），实际上也很nb。

实现

核心思想是将两个多项式先转换为点值表示法，把他们乘起来，再转换回多项式然后输出。

第一步

转换成点值表示（DFT + 蝴蝶变换）
如果随便带n个点进去的话是 $O(n^2)$ 的，太慢了，所以需要一种炫酷的表示方式。

第二步

将卷积的点值表示转换回多项式(IFFT)
如果只是单纯的暴力的话可以直接高斯消元，但显然很慢。

最后

迭代优化
我们会发现这个FFT是需要，递归的，常数有些大，又要一个常数没那么大的方法。
以上三个难题就是FFT的全部，由于实在是太长了，所以我直接放一个链接自己去看吧。
https://blog.csdn.net/enjoy_pascal/article/details/81478582

例题 P3803 【模板】多项式乘法（FFT）

#include<iostream>
#include<cstdio>
#include<cmath>
#define for1(i,a,b) for(int i = a;i <= b;i ++)
using namespace std;
const int MAXN=1e7+10;

const double pi=acos(-1.0);
struct fushu
{
    double x,y;
    fushu (double xx=0,double yy=0)
	{
		x=xx;
		y=yy;
	}
}a[MAXN],b[MAXN];

fushu operator + (fushu a,fushu b)
{ 
	return fushu(a.x+b.x , a.y+b.y);
}
fushu operator - (fushu a,fushu b)
{ 
	return fushu(a.x-b.x , a.y-b.y);
}
fushu operator * (fushu a,fushu b) //这个是叉乘，不是高中的点乘 
{ 
	return fushu(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);
}

int N,M;
int l,r[MAXN];
int mx=1;
void fft(fushu *A,int type)
{
    for1(i,0,mx)//把数字放到最后的位置 
        if(i<r[i]) 
			swap(A[i],A[r[i]]);
			
    for(int mid=1;mid<mx;mid<<=1)//待合并区间的中点
    {
        fushu wn( cos(pi/mid) , type * sin(pi/mid) ); //type如果是-1 就是IFFT 
		//单位根 直接背 
		
        for(int R = mid << 1,j = 0;j < mx;j += R)//R是区间的右端点，j表示前已经到哪个位置了 
        {
            fushu w(1,0);//幂 
            for(int k = 0;k < mid;k ++, w = w * wn)//枚举左半部分 
            {
                 fushu x = A[j + k], y = w * A[j + mid + k];//蝴蝶效应 
                A[j + k] = x + y;
                A[j + mid + k] = x - y;
            }
        }//这一段我也没想明白，就留着题解的注释 
    }
}
int main()
{
    int n,m;
    cin>>n>>m;
    for1(i,0,n) cin >>a[i].x;
    for1(i,0,m) cin >> b[i].x;
    while(mx <= n + m) 
    {
		mx<<=1;
		l++;
	}
    for1(i,0,mx)
        r[i]= ( r[i / 2] / 2 ) | ( (i & 1) << (l - 1) ) ;
    //落实数字的最后位置，建议直接背 
    fft(a,1);
    fft(b,1);
    
    for1(i,0,mx)
		a[i] = a[i] * b[i];
		
    fft(a,-1);//IFFT
    
    for1(i,0,n + m)
        printf("%d ",(int)(a[i].x / mx + 0.5));//四舍五入 
    return 0;
}

应用【模板】A*B Problem 升级版（FFT 快速傅里叶变换）

不难想到，一个n位十进制数其实就是一个n次多项式，并且x取的是10

#include<bits/stdc++.h>
#define for1(i,a,b) for(int i=a;i<=b;i++)
using namespace std; 

typedef complex<double> cp;
const double pi=acos(-1.0);
const int N = 4e6 + 5;
int n;
cp a[N],b[N];
int rev[N],ans[N];
string s1,s2;
//k表示转化成二进制的位数
void init(int k)//初始化每个位置最终到达的位置 
{
    int len=1<<k;
	for(int i=0;i<len;i++)
	rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
}

//a表示要操作的数组，n表示序列长度
//若flag为1表示FFT，为-1则为IFFT
void fft(cp *a,int n,int flag)
{ 
    for1(i,0,n-1) 
	{
	 //i小于rev[i]时才交换，防止同一个元素交换两次 
		if(i<rev[i])
			swap(a[i],a[rev[i]]);
	}
	
	for(int h=1;h<n;h*=2)//折半转换 
	{
		cp wn = exp(cp(0 , flag * pi / h));//求单位根w_n^1 
	 	for(int j = 0;j < n;j += h * 2)//j表示合并到了哪一位
	 	{
	  		cp w(1,0);
	   		for1(k,j,j + h - 1)//只扫左半部分，得到右半部分的答案
	   		{
	    		cp x = a[k];
	    		cp y = w * a[k + h];
        		a[k] = x + y;   
 	    	   	a[k+h] = x - y;
        		w *= wn; 
				//求w_n^k 
	   		}
	 	}
	}
	 //判断是否是FFT还是IFFT 
	if (flag == -1)
	for1(i,0,n-1)
    a[i]/=n;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin>>s1>>s2;
	
	int len1 = s1.size();
	int len2 = s2.size();
	
	string ji = "";
	if(len1 != len2)
		for1(i,1,abs(len1-len2))
			ji += '0';
			
	if(len1>len2)
		s2 = ji + s2;
	if(len2>len1) 
		s1 = ji + s1;
		
	n = s1.size();
	
    for1(i,0,n-1)
		a[i] = (double)(s1[n-i-1]-'0');
	for1(i,0,n-1) 
		b[i] = (double)(s2[n-i-1]-'0');
	
	 
	int k=1,s=2;
 	while((1<<k)<2*n-1)
	{	
	 	k++;
		s <<= 1;
	}
	init(k);
    fft(a,s,1);
    fft(b,s,1);
    
    for1(i,0,s-1)
    a[i]*=b[i];
    
    //IFFT 
    fft(a,s,-1);
     
    //取实数四舍五入
    for1(i,0,s-1)
    {
		ans[i] += (int)(a[i].real() + 0.5);
		ans[i + 1] += ans[i] / 10;
		ans[i] %= 10;
	}
	while(! ans[s] && s > -1)
		s --;
	if(s == -1)
		cout<< 0;
	else
		for(int i = s;i >= 0;i --)
			cout << ans[i];
	return 0;
}

总结

以后出去装B，甚至不说快速傅里叶变换，要说“离散傅立叶变化
带蝴蝶变换接快速傅立叶逆变换的迭代优化”，这B格不就起来了。

NTT

定义

求

\[h(x) = f(x)g(x) \mod p \]

其中 $p$ 为质数

解决

经过一番花里胡哨的证明（感兴趣可以自己去找），我们会发现它和FFT唯一的区别就是他不使用单位根，使用的是原根，其他没有区别。

狄利克雷卷积

不知道有什么用，等用到再学
https://www.cnblogs.com/Plozia/p/16156789.html#:~:text=狄利克雷卷积定义： t %3D f ∗ g%2C t (n),> 1 f (d) g (n d) 。

生成函数函数与数列之间的桥梁

定义

我们称

\[g(x)=a_0+a_1x+a_2x^2 +a_3x^3 + . . . a_{n}x^n \]

是序列

\[\{ a_1,a_2,a_3,...,a_n \} \]

的生成函数（也叫母函数，但是生成函数听起来帅一点）

接下来会引入一个非常炸裂的东西：无穷。
我们思考

\[f(x) = 1 + x + x^2 + x ^ 3 + ..... \]

，他很显然是序列 $ {1,1,1,1,1.....} $ 的生成函数，同时是一个等比数列
，所以根据等比数列求和公式，得到：

\[\frac{1}{1 - x} = 1 + x + x^2 + x ^ 3 + ..... \]

\[a = [1,1,1,1,...] \]

我们乍一看似乎没问题，但是我们带个数进去看看，
假如 $ x = 2 $ 我们会惊讶的发现函数居然变成了 $-1$ !
这母庸置疑是极度反常识的，无穷个整数相加却得到了一个负数（当时学的时候我都给整不会了）。
这是因为无穷是一个无法用概念去理解的东西，只能通过计算之类的去认识，所以没法用直觉去思考的,待会还有一大堆其他的这种情况的东西出现。
此时，我们自然而然地想到，其实任何一个函数都是可以用数列来表示的，都存在一个数列的生成函数是它。

性质

而我们自然也可以通过对函数操作从而达到变化数列的目的。

还有一个很有意思的是，乘上数列 $[1,1,1,1,1....]$ 相当于求了一次前缀和，如
生成[1,2,3,4,...]

\[[1,1,1,1...] * [1,1,1,1...] = \frac{1}{(1 + x)^2} \]

生成[1,3,6,10,...]

\[[1,1,1,1...] * [1,2,3,4...] = \frac{1}{(1 + x)^3} \]

如何生成[1,4,9,16...]

\[[0,1,3,6...] + [1,3,6,10,...] = \frac{x+1}{(1 + x)^3} \]

(数列右移)

例题 P2000 拯救世界

由于这玩意最后需要用NTT，所以我直接用python摆烂了

from decimal import *
getcontext().prec = 1000000
n = Decimal(input())
print((n + 1) * (n + 2) * (n + 3) * (n + 4) / 24)

于 2023/3/7 更新

posted @ 2023-03-07 20:40 yyx525jia 阅读(37) 评论(0) 收藏举报

刷新页面返回顶部

yyx525jia