寒假集训——基础数论2 欧拉函数,阶,原根以及BSGS
欧拉函数
定义
欧拉函数:正整数n的欧拉函数\(φ(n)\)的值等于不超过n且与n互质的正整数的个数。
例如:
因为1,3,5,7均和8互质;
性质
1.
对于质数n
2.
对于\(n=p^k\)
3.
对于\(gcd(n,m)=1\)即$ n \perp m $
4.
对于 $ n = p_1^{k_1} p_2^{k_2} p_3^{k_3} ..p_n^{k_n} $ (通过唯一分解定理分解,\(p_1,p_2,...p_n\)都是质数),时,
即
当$ n = \prod p_i^{k_i} $时,
补:
阶
定义
若 \((a, m) = 1\) ,使得 \(a^l mod m = 1\) 的最小的正整数l,我们称为a关于模m的阶
注:此处的 \((a, m) = 1\) 就是 \(gcd(a, m) = 1\)
我们会发现在 2在模7的意义下的n次方时有一个循环的 \({2,4,1,2,4,1,...}\),其中,这里的 \({2,4,1}\) 就是 2在模7的意义下的剩余系,而我们称3是2在模7意义下的阶(也可以叫循环节?),写作
于2023.1.8 更新
性质
1.
当
时,可推出
首先我们先设 $ a^{k} \equiv 1 ( \bmod m) $ ,$ k= x * ord_m a+y $ ,然后我们会发现 $ a^{ x*ord_m a+y } \equiv a^{ord_ma} \equiv 1 ( \bmod m) $ ,而且 $ ord_ma $是最小的,所以y=0.
由性质1可以推出 $$ ord_ma | φ(n) $$
2.

原根
定义
当
时, $ ord_m a$ 称为a关于m的原根
如3是7的一个原根:
性质
1.
我们不难发现,此时剩余系中就是 $ {1,2,3,4,5,6} $,是所有与7互质的数。
因此我们可以使用原根+快速幂快速求出一个数的所有与它互质的数,复杂度应该是 \(O( \log n )\)(在知道原根是什么的前提下)
2.
一个数有 $ φ(φ(n)) $个原根

这么好用的东西,当然得用。所以我们此时应该思考如何求原根
求原根
思路
我们会发现比较难想
,古人云:

所以我们应该向着什么不是原根去是思考什么是原根
设求p的原根
一个数i不是原根,说明他的阶 \(ord_p i\) 一定是小于 $ φ(n) $的,我们有可以根据阶的性质1的推论:
,可以发现一个数i不是p的原根,代表该数一定有如下性质:
设
,有
我们只需要从小到大找,找到的第一个不符合此条件的数就是最小原根了。
同时根据性质三,我们只需要先求出最小原根,然后乘方求出其他原根
于2023.1.10更新
求欧拉函数
此时我们的难点来到了如何求欧拉函数
我们观察欧拉函数的性质,不难(挺难的,反正我没想到)想到,他应该可以使用筛法筛出来,并且我们使用最快的线性筛
for1(i,2,n)
{
if(a[i] == 0)
ans[++ji] = i;
for(int j = 1;j <= ji && ans[j] *i <= n;j++)
{
a[ans[j] *i] = 1;
if(ans[j] % i == 0) break;
}
}
我们会发现,其实线筛把一个数字分成了三类:
1.质数,在第一个if语句那里
2.最小质因数不是ans[j]的数,就是在 a[ans[j] *i] = 1;这里
3.最小质因数是ans[j]的数,在第二个if语句那里
此时,我们也对欧拉函数做一个这样的分类,可以分出(设 ans[j]=k)
1.质数,
2.最小质因数是ans[j]的数 $ gcd(i,k)=1 $ ,
3.最小质因数不是ans[j]的数 $ gcd(i,j) \neq 1 $,
第一和第二种分类是显然的,对于第三种分类,
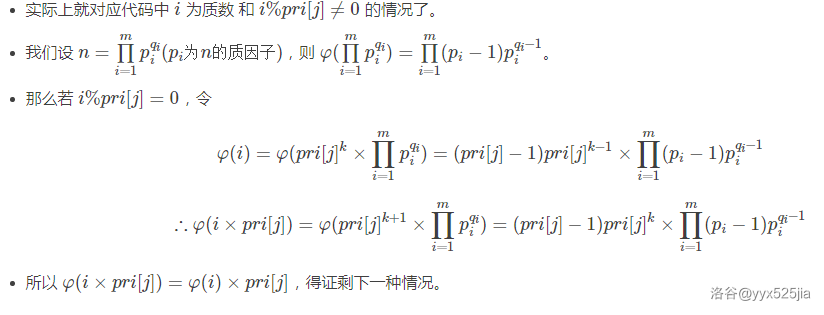
由此我们就可以得到线性筛求欧拉函数的代码
for1(i,2,n)
{
if(a[i] == 0)
{
ans[++ji] = i;
phi[i]=i-1;//第一类
}
for(int j = 1;j <= ji && ans[j] *i <= n;j++)
{
a[ans[j] *i] = 1;
if(ans[j]%i==0)//第三类
{
phi[i*ans[j]]=ans[j]*phi[i];
}
phi[i*ans[j]]=phi[i]*phi[ans[j]];//第二类
}
}
总结/代码
此时我们所有求原根的工具都大功告成了,列出清单:
1.线性筛求欧拉函数。
2.对要求的p的欧拉函数 \(φ(p)\) 做质因数分解
3.从一开始枚举,寻找
4,求出p的欧拉函数的欧拉函数具体是哪些数 $ s|gcd(φ(φ(p)),s)=1 $
5.快速幂
6.根据最小原根和4,5求出其他原根
只能说,不愧是蓝题,在推导了这么久之后还需要打那么多代码(其实也没多少)
于2023.1.11更新
#include<bits/stdc++.h>
#define ll long long
#define for1(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
int t,cnt,tot,jians;
int fz[2000005],ans[2000005];
int zs[2000005],rt[3000005];
int q[3000005],phi[2000005];
void init () {
phi[1]=1;
for1(i,2,2000005)
{
if (!q[i])
{
zs[++tot]=i;
phi[i]=i-1;
}
for (int j=1;j<=tot&&zs[j]*i<=2000005-10;j++)
{
q[i*zs[j]]=1;
if (i%zs[j]==0)
{
phi[i*zs[j]]=phi[i]*zs[j];
break;
}
phi[i*zs[j]]=phi[i]*(zs[j]-1);
}
}
rt[2]=rt[4]=1;
for1(i,2,tot)
{
for (int j=1;(1ll*j*zs[i])<=2000005-10;j*=zs[i]) rt[j*zs[i]]=1;
for (int j=2;(1ll*j*zs[i])<=2000005-10;j*=zs[i]) rt[j*zs[i]]=1;
}
return;
}
int gcd (int a,int b)
{
return (b==0?a:gcd(b,a%b));
}
int ksm(int a,int b,int p)
{
int ji=1;
while (b) {
if (b%2==1) ji=(1ll*ji*a)%p;
a=(1ll*a*a)%p;
b>>=1;
}
return ji;
}
void fenjie (int p)
{
for (int i=2;i*i<=p;i++)
{
if (p%i==0)
{
fz[++cnt]=i;
while (p%i==0) p/=i;
}
}
if (p>1) {fz[++cnt]=p;}
return;
}
bool chk (int x,int p)
{
if (ksm(x,phi[p],p)!=1)
return false;
for (int i=1;i<=cnt;i++)
if (ksm(x,phi[p]/fz[i],p)==1)
return false;
return true;
}
int find (int p)
{
for1(i,1,p-1)
if (chk(i,p))
return i;
return 0;
}
void gt (int p,int x)
{
int ji=1;
for1(i,1,phi[p])
{
ji=(1ll*ji*x)%p;
if (gcd(i,phi[p])==1)
{
ans[++jians]=ji;
}
}
return;
}
int main ()
{
int p;
init();
scanf("%d",&t);
for1(k,1,t)
{
int d;
scanf("%d%d",&p,&d);
if (rt[p])
{
jians=cnt=0;
fenjie(phi[p]);
int ji=find(p);
gt(p,ji);
sort(ans+1,ans+jians+1);
printf("%d\n",jians);
for (int i=1;i<=jians/d;i++) printf("%d ",ans[i*d]);
printf("\n");
}
else
printf("0\n\n");
}
return 0;
}
于2023.1.12 更新
BSGS
思路
对于一个同余方程
(p是质数)
已知 \(a,b,p\) 求最小正整数x
我们首先先看一下BSGS的全称

我们再看看翻译(假如我们看不懂英文)

。。。
开个玩笑,实际上这个算法叫做
回到正轨,首先我们由上面的阶的性质可以知道 $ x \le φ(p) $ 但是我们为了方便,就换成 $ x \le p $
于2023.1.13 更新
然后我们思考,能不能使用一种类似倍增的方法来枚举这个x?
于是数学家们就想出了这个算法
首先设
其中$ t=\sqrt p $,很容易发现, \(j\) 的枚举范围是 \([1, \sqrt p -1 ]\),
此时我们进行一些变换。
先把 $ b * a^{j} $ ,枚举 $ [1, \sqrt p -1] $ 算出来
然后全部丢进(STL容器)map里面,然后直接枚举i,算出 $ a^{i * t} $ ,再看看map里面有没有出现过就可以了。
当然,记得模p,还有处理一些特判(比如 $a=1,b>p $ )之类的
此时我们就可以看出这个方法到底为什么叫BSGS了, 里面的i其实就是 Giant step ,j就是 Baby step
代码
#include <bits/stdc++.h>
#define ll long long
#define for1(i,a,b) for(register ll i=a;i<=b;i++)
using namespace std;
map<ll, ll> vis;
ll ksm(ll x, ll y, ll z) {
if (!y)
return 1;
ll ans = 1;
while (y) {
if (y % 2 == 1)
ans = (ans * x) % z;
x = (x * x) % z;
y /= 2;
}
return ans;
}
ll bsgs(ll a, ll b, ll p) {
if (a % p == 0 || b % p == 0)
return -1;
if (b == 1)
return 0;
ll t = sqrt(p) + 1;
vis.clear();
for1(i, 0, t - 1)
vis[(ll)b * ksm(a, i, p) % p] = i;
a = ksm(a, t, p);
if (!a) {
if (b == 0)
return 1;
else
return -1;
}
for1(i, 1, t) {
ll val = ksm(a, i, p);
int j;
if (vis.find(val) == vis.end())
j = -1;
else
j = vis[val];
if (j >= 0 && i * t - j >= 0)
return i * t - j;
}
return -1;
}
int main() {
int T, p, a, b;
cin >> p >> a >> b;
ll ans = bsgs(a, b, p);
if (ans == -1 )
printf("no solution\n");
else
printf("%lld\n", ans);
return 0;
}
小逝牛刀
P3846 [TJOI2007] 可爱的质数/【模板】BSGS
就是模板题
P4028 New Product
其实相当于模板(双倍经验狂喜)但是有一些东西要特判,比如说a=1之类的
于2023.1.16 更新
扩展BSGS
我们注意到BSGS有一个前提条件,就是p需要是质数,那如果p不是质数,或者 $ gcd(a,p) \neq 1 $,那么此时我们的BSGS就不适用了,需要进行一些拓展。
我们想到,如果我们把式子转化成之前的那种情况,即 $ gcd(a,p) = 1 $,那不就又可以使用了吗,所以开始尝试。
先把同余方程转化成普通的方程
设 $ gcd(a,p)=d $,转换成
此时我们再转换成 $ a^{,} = a^{x-1} , p^{,} = \frac{p}{d} , n^{,} = \frac{n}{d} $,那方程就变成了
然后我们一直这样转换,最后就变成
注意:d是之前的所有的d的乘积
再转换回来
注:此时的 $ \frac{a^{cnt}}{d} $是常数,因为d与 $ a^{cnt} $是已知的。
此时 $ gcd(a.p)=1 $,就可以用普通的BSGS了,而之前的d只需要使用递归就可以了。
于2023.1.18 更新


 浙公网安备 33010602011771号
浙公网安备 33010602011771号