寒假集训——基础数论1 sigma本质及数列分块

目录

• 开篇 \(\sum\)的本质
  • 求和的运算定律
    • 分配律
    • 结合律
    • 换元法
  • 应用（逝逝看）
    • 例1
    • 例2
    • 例3
    • 例4
    • 例5
  • 数列分块
    • 思路
    • 实战（试试就逝世）P2261 [CQOI2007]余数求和

开篇 \(\sum\)的本质

\(\sum\) 其实可以理解为for循环

例如 $$ \sum_{i = 1}^{n} i $$

其实就是代码中

int ans=0;
for(int i=1;i<=n;i++) ans+=a[i];

ans的值

求和的运算定律

分配律

\[\sum_{i \in K} c * i = c * \sum_{i \in K} i \]

很简单，不解释
反过来同理

结合律

\[\sum_{i \in K} a_i + \sum_{i \in K} b_i = \sum_{i \in K} (a_i + b_i) \]

反过来同理

换元法

\[\sum_{i \in K} a_i = c * \sum_{p(i) \in K} a_{p(i)} \]

可以理解为换了一个枚举方法，具体例子见例1

\[[i=3] \]

意思是如果 \(i\) 等于3就返回1，其他时候返回0，相当于if语句，一般用于

\[\sum_{i = 1}^{n} i * [i = 3] \]

这种类型的式子
其实就相当于代码

int ans=0;
for(int i=1;i<=n;i++) 
    if(i==3)
    ans+=a[i];

应用（逝逝看）

三个例子本质上其实都是在简化操作，可以理解为在打代码时优化常数

例1

\[\sum_{k = 1}^{n} k \]

求递推式

\[\sum_{k = 1}^{n} k \]

换元

\[=\sum_{k = 1}^{n} n-k+1 \]

拆开

\[=\sum_{k = 1}^{n} n+1 - \sum_{k = 1}^{n} k \]

不难发现前面那个 $\sum $ 其实就是 $ n * （n+1）$，后面那个 $\sum $ 其实就是求和公式

\[\sum_{k = 1}^{n} k = n * (n+1) - \sum_{k = 1}^{n} k \]

合并同类项

\[2\sum_{k = 1}^{n} k = n * (n+1) \]

系数化简

\[\sum_{k = 1}^{n} k = \frac{n * (n+1)}{2} \]

既可
就这样，一个 $ O(n) $ 的循环被我们化简成了 \(O(1)\)

例2

\[\sum_{k = 1}^{n} (2^k*k) \]

求递归式

\[设 S_n=\sum_{k = 1}^{n} (2^k*k) \]

把k换成k-1

\[= \sum_{k = 0}^{n-1} (2^{k+1} * (k+1)) \]

展开（k+1）

\[= \sum_{k = 0}^{n-1} (2^{k+1} * k + 2^{k+1}) \]

提出 \(2^{k+1}\)

\[= 2\sum_{k = 0}^{n-1} (2^{k} * k) + \sum_{k = 0}^{n-1} 2^{k+1} \]

把后面那个$ \sum $ 的 $ k+1 $ 换回k，前面那个 $ \sum $ 可以发现 $ k=0 $ 时不对答案做贡献，所以可以直接把前面的 $ k $ 调成从 \(1\) 开始

\[= 2\sum_{k = 1}^{n-1} (2^{k} * k) + \sum_{k = 1}^{n} 2^{k} \]

不难发现后面那个 \(\sum\)其实就是等比数列之和，直接用公式 $ \frac{a_1-a_n*q}{1-q}$

\[= 2\sum_{k = 1}^{n-1} (2^{k} * k) +2^{n+1}-2 \]

不难发现前面那个 \(\sum\)其实就是 \(S_{n-1}\)

\[= 2S_{n-1} +2^{n+1}-2 \]

显然我们再使用矩阵加速

初始矩阵

\[\begin{bmatrix} a_0 \ 2^2 \ 2 \end{bmatrix} \]

\(a_0\)就是0
加速矩阵

\[\begin{bmatrix} 1 \ 0 \ 0 \\ 1 \ 2 \ 0 \\ -1 \ 0 \ 1 \\\end{bmatrix} \]

就可以让它从 $ O( n) $ 变成 $ O( \log n) $

例3

\[S_n=\sum_{i = 1}^{n} \sum_{j = i}^{n} a_ia_j \]

化简

\[S_n=\sum_{i = 1}^{n} \sum_{j = i}^{n} a_ia_j \]

再加入一个 \(S_n\)+换元法

\[2S_n=\sum_{i = 1}^{n} \sum_{j = i}^{n} a_ia_j + \sum_{i = 1}^{n} \sum_{j = 1}^{i} a_ia_j \]

至于为什么换元，如图

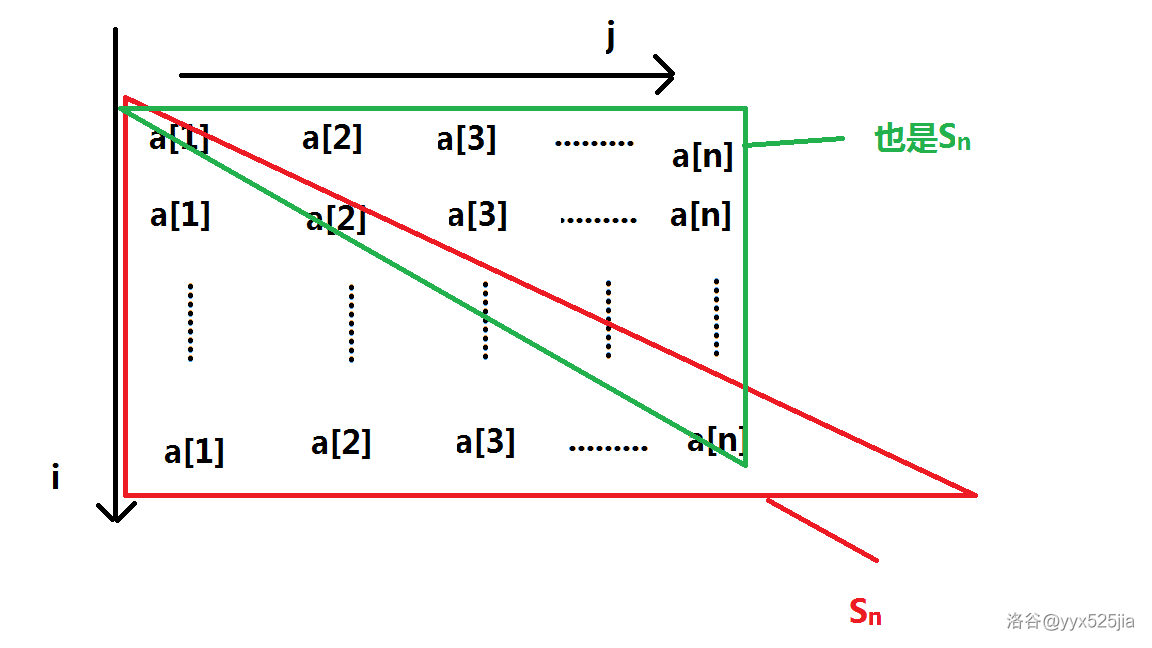
合并

\[2S_n=\sum_{i = 1}^{n} \sum_{j = i}^{n} a_ia_j * ([j<=i]+[i<=j<=n]) \]

很明显，除了当i==j时 \(([j<=i]+[i<=j<=n])\)中是2，其他时候都是1，所以可以简化成

\[2S_n=\sum_{i = 1}^{n} \sum_{j = 1}^{n} a_ia_j + \sum_{i = 1}^{n} a_i \]

对于第二个 \(\sum\) 而言, $ a_i$相当于是常数，可以提出来

\[2S_n=\sum_{i = 1}^{n} (a_i * \sum_{j = 1}^{n} a_j) + \sum_{i = 1}^{n} a_i \]

此时我们如果提前算出$ \sum_{i = 1}^{n} a_i $并且设为 \(S_n\)
那么公式就变成了

\[2S_n=\sum_{i = 1}^{n} (a_i * S_n) + S_n \]

提系数

\[S_n=\frac{1}{2}\sum_{i = 1}^{n} (a_i * S_n) + \frac{1}{2}S_n \]

就这样，一个 $ O(n^2) $ 的循环被我们化简成了 \(O(n)\)

于2023.1.7更新

例4

\[\sum_{k=1}^{n} \lfloor \sqrt k \rfloor \]

化简

我们稍微枚举一下，就会发现这样一个性质

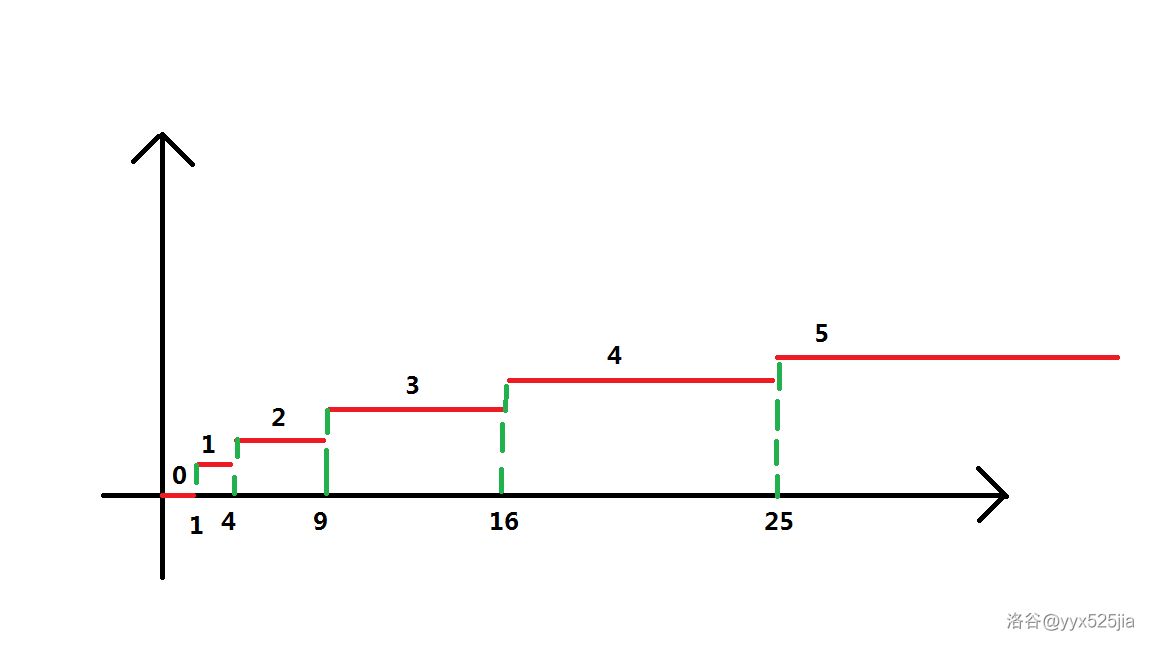
这个数列是一段一段的，而且第i段的长度是 \(i^2-(i-1)^2\)，第i段的值是 $ i-1 $,那么我们可以直接化简成

\[\sum_{k=1}^{ \lfloor \sqrt n \rfloor } ((k-1)*(k^2-(k-1)^2)) + (n-(\lfloor \sqrt n \rfloor)^2 )* \lfloor \sqrt n \rfloor \]

\(O(n)\) 优化成 \(O(n \sqrt n)\)(事实上要求根号应该不是常数)

例5

\[\sum_{k=1}^{n} gcd(n,k) \]

注：此处的gcd指最大公因数
化简

我们稍微使用换元法，会得到

\[\sum_{d|n} (d * \sum_{i=1}^{n} [gcd(n,i)==d]) \]

注：$ a|b $的意思是：a为除数，b为被除数，即a|b（|是整除符号）。b叫做a的倍数，a叫做b的约数（或因数）。

[]中同除d

\[\sum_{d|n} (d * \sum_{i=1}^{n} [gcd(\frac{n}{d},\frac{i}{d})==1]) \]

把 \(\frac{i}{d}\) 设成i

\[\sum_{d|n} (d * \sum_{i=1}^{\frac{n}{d}} [gcd(\frac{n}{d},i)==1]) \]

此时我们发现 $ \sum_{i=1}^{\frac{n}{d}} [gcd(\frac{n}{d},i)==1]) $其实本质上就是在求 \(\frac{n}{d}\)的欧拉函数（后面会学），所以我们就可以化成

\[\sum_{d|n} (d * φ(\frac{n}{d})) \]

\(O(n\log n)\) 优化成 \(O(n)\)(也许是 \(O( \log n )\) )

通过这五个例子，足以对于\(\sum\)有一个新的认识（只是我是过陋寡闻大开眼界）

数列分块

思路

我们回想之前的例4，我们应该会有一个疑问：

数学家们和百度告诉我们：

所以我们可以设一个

\[\sum_{k=1}^{n}f(i) \lfloor \frac{n}{i} \rfloor \]

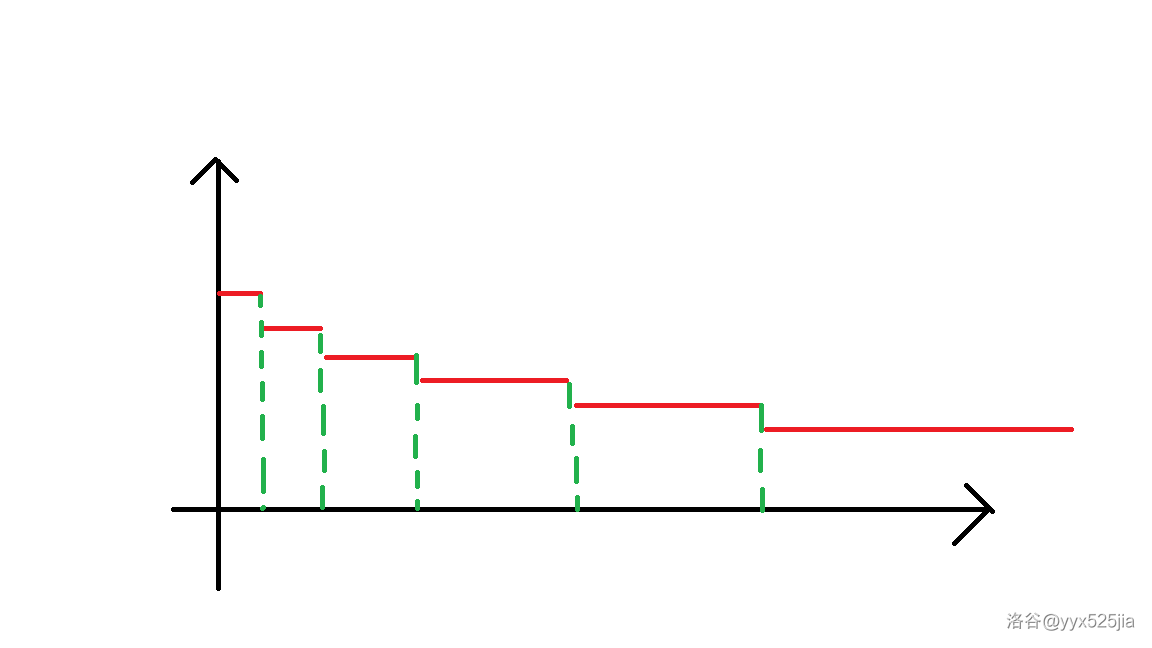
\(f(i)\)可以是任意一个函数

那么此时我们自然贪心的想要一个对于这一类式子的统一的优化，我们可以仿造之前对例4的处理，仍然把它分成整块区间的区间长度*区间值（其实也就是 \(f(i)\) ） ，至于被从中间截断的，我们直接特判就完事，我们现在需要的是：

我们关注到一个性质: $ 一段区间的函数值是相同的。$
所以我们就可以列出一个等式

\[\lfloor \frac{n}{l} \rfloor = \lfloor \frac{n}{r} \rfloor \]

稍加化简，可以得到

\[r = \lfloor \frac{n}{\lfloor \frac{n}{l} \rfloor} \rfloor \]

就这样，我们得到了l和r之间的关系式，因此，一个普遍的优化就这样推出来了

实战（试试就逝世）P2261 [CQOI2007]余数求和

题意：
给出正整数 n 和 k，请计算

\[G(n, k) = \sum_{i = 1}^n k \bmod i \]

注：mod就是%
给出n,k
\(对于 100\% 的数据，保证 1 \leq n, k \leq 10^9\)
首先，我们应该知道%的本质

\[a\bmod b=a-b* \lfloor \frac{a}{b} \rfloor \]

所以我们直接返璞归真

\[G(n, k) = \sum_{i = 1}^n (k-i* \lfloor \frac{k}{i} \rfloor) \]

使用把k抽出来

\[G(n, k) = \sum_{i = 1}^n k-\sum_{i = 1}^n (i* \lfloor \frac{k}{i} \rfloor) \]

把k化简

\[G(n, k) = n*k-\sum_{i = 1}^n (i* \lfloor \frac{k}{i} \rfloor) \]

我们发现，这不就是前面讲的那个数列分块嘛，所以我们自然而然的使用优化。
总共有k种取值，所以时间复杂度就是\(O(\sqrt k)\)的。
然后就直接模拟按照刚刚的推论做就完事
注意开long long

#include<bits/stdc++.h>
#define for1(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define mp(a,b) make_pair(a,b)
using namespace std;
ll n,k;
int main() 
{
    cin>>n>>k;
    ll ans=n*k;
    ll l=1,r=0;
    while(l<=n) 
	{
		l=r+1;
        if(k/l!=0) 
		    r=min(k/(k/l),n); 
        else //当k/l等于0时意味着已经触碰到了边界n 
		    r=n;
        ans-=(k/l)*(r-l+1)*(l+r)/2;
    }
    cout<<ans<<endl;
    return 0;
}

于2023.1.8更新