动态规划--国王和金矿

动态规划--国王和金矿

封面图片来自程序员小灰 漫画：什么是动态规划？（整合版）, 最近阅读了小灰的系列文章，感觉动态规划这篇讲的挺好的，循序渐进；动态规划这块我是没学透，简单的还好些，一旦题中的变量大于1时，就开始懵逼了。比较纠结的是如下几个问题：

• 动态规划与排列组合的关系
• 动态规划与递归的关系
• 怎样才能找出最优子结构，并写出状态转移式(递归式)

动态规划的几个要素为：

• 最优子结构
• 状态转移公式
• 边界

下面通过分析国王和金矿这个题目来体会一下。

题目：有一个国家发现了5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半金矿。要求用程序求解出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿？

（注：该问题也是背包问题的另一种形式）

 

方法一：每个金矿要么挖要么不挖，共有2^5组合方法。通过枚举这些组合，选出最大产出的组合。组合方式可用一棵树示意。

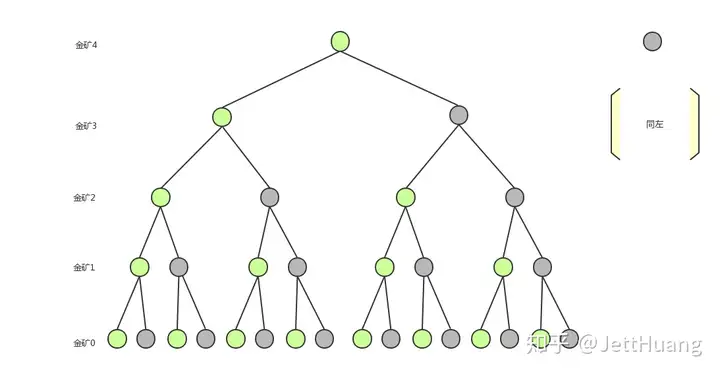
（注：绿色表示挖，灰色表示不挖）

自顶向下进行遍历分支(从根部到叶子的路径为一种组合情况)，算出分支的人力和产出，得出最大的产出那种组合。

源码如下：

// 使用排列组合方法(通过递归枚举)找出最优解
//

#include <stdio.h>
#include <stdlib.h>


#define MAX_MINES		5

// 金矿信息
struct FGoldMineMeta
{
	int		Golds;  // 金量
	int		Workers;// 工人
};

// 递归遍历的Context
struct FTravelContext
{
	bool  BestCombination[MAX_MINES];
	int	  BestOutputVal;

	bool  TravelCombination[MAX_MINES];
	int	  TravelOutputVal;

	int	  RemainWorkerNum;

	FTravelContext(int InWorkerNum)
		: BestOutputVal(0)
		, TravelOutputVal(0)
		, RemainWorkerNum(InWorkerNum)
	{
		for (int k = 0; k < MAX_MINES; k++)
		{
			BestCombination[k] = TravelCombination[k] = false;
		}
	}
};

void RecursiveCombination(const FGoldMineMeta InMines[MAX_MINES], FTravelContext &InCtx, const int InDepth, const bool InbDig)
{
	bool SavedDig = InCtx.TravelCombination[InDepth];
	int  SavedTravelOutputVal = InCtx.TravelOutputVal;
	int  SavedRemainWorkerNum = InCtx.RemainWorkerNum;

	bool bStopTravel = false;

	InCtx.TravelCombination[InDepth] = InbDig;
	if (InbDig)
	{
		const int WorkerNum = InMines[InDepth].Workers;
		const int GoldNum = InMines[InDepth].Golds;
		if (InCtx.RemainWorkerNum >= WorkerNum)
		{
			InCtx.TravelOutputVal += GoldNum;
			InCtx.RemainWorkerNum -= WorkerNum;
		}
		else
		{
			bStopTravel = true;
		}
	}
	bStopTravel = bStopTravel || (InDepth == 0);
	if (bStopTravel)
	{
		// 进行结算
		if (InCtx.TravelOutputVal > InCtx.BestOutputVal)
		{
			InCtx.BestOutputVal = InCtx.TravelOutputVal;
			for (int k = 0; k < MAX_MINES; k++)
			{
				InCtx.BestCombination[k] = InCtx.TravelCombination[k];
			}
		}
	}
	else
	{
		RecursiveCombination(InMines, InCtx, InDepth-1, true);
		RecursiveCombination(InMines, InCtx, InDepth - 1, false);
	}

	InCtx.TravelCombination[InDepth] = SavedDig;
	InCtx.TravelOutputVal = SavedTravelOutputVal;
	InCtx.RemainWorkerNum = SavedRemainWorkerNum;
}

void FindBestCombinationOfMines(const FGoldMineMeta InMines[MAX_MINES], int InWorkerNum)
{
	FTravelContext Ctx(InWorkerNum);

	RecursiveCombination(InMines, Ctx, MAX_MINES-1, true);
	RecursiveCombination(InMines, Ctx, MAX_MINES-1, false);
	
	// display result.
	printf("排列组合 Max Dig Golds: %d\n", Ctx.BestOutputVal);
	printf("Solution is: ");
	for (int k = 0; k < MAX_MINES; k++)
	{
		if (Ctx.BestCombination[k])
		{
			printf("金矿%d  ", k);
		}
	}
	printf("\n");
}

int main()
{
	FGoldMineMeta  Mines[MAX_MINES] = {
		{ 400, 5},
		{ 500, 5},
		{ 200, 3},
		{ 300, 4},
		{ 350, 3}
	};

	FindBestCombinationOfMines(Mines, 10);

	system("pause");
    return 0;
}

方法二：动态规划

下面一般地描述上述问题，令有金矿N座，矿产量对应为数组G[N], 使用工人数量对应为数组W[N], 总共工人数为M。金矿的标号分别为0, 1, 2, ... N-1。

函数F(x, y)表示 有y个工人、x座金矿的条件下，最大的产出量。那么针对标号为N-1的金矿有两种选择: 开采、不开采.

1. 开采: 则得到的矿量为G[N-1]、占用工人数W[N-1]; 剩下的N-1个矿还可以用M-W[N-1]个工人； 这种情况下能够获得最大总产量为 G[N-1] + F(N-1, M-W[N-1]);
2. 不开采: 则得到的矿量为0，占用工人数0; 剩下的N-1个矿还可以用M个工人; 这种情况下能够获得的最大总产量为 F(N-1, M)

所以： F(N, M) = max( F(N-1, M), F(N-1, M-W[N-1]) + G[N-1])

边界情况为：

• F(1, M) = G[0] M>= W[0],
• F(1, M) = 0, M < W[0]

特殊考虑: F(x, y)退化为 F(x-1, y) 如果 y < G[x-1] (挖这个矿人手不够)。

根据上面的状态公式，可用下图示意:

（注: 绿色表示挖，灰色表示不挖）

我们可以发现，这里仍是考虑了每个矿是否要开采，进而体现可能的组合。

这里又有两种方式进行求解：

1. 【自顶向下再向上】根据上述公式，采用递归进行后序遍历该树。其实这个跟上面使用排列组合的方法求解类似，它们的区别在于：排列组合使用的是先序遍历，相当于先累积结点值，然后比较分支路径和大小；而这个是先比较分支的大小，择优上报，最终PK出最大值。
2. 【自底向上递推】从底部边界情况，根据状态迁移公式递推到顶部。这种才算“动态规划”算法。然后此题中存在2个变量<金矿个数, 工人个数>，我们看到图中每层的值分配情况，虽然每层的金矿值是固定值，但是工人数的值是不固定的，所以需要求出所每层 有工人个数的情况，以便上层的公式中对子公式F(n,m)的值查找。我们不知道上层要查询的F(n,m)的 m是几，所以保险起见，会计算所有的m值情况[1, M]。具体演示过程请 参考程序员小灰 漫画：什么是动态规划？（整合版）的图表演示。

源码如下：

// 使用动态规划算法，从边界向目标递推.
// 如果仅求出最大的产出值，只需要2行表进行交替;
// 如果需要求出最终要挖哪些金矿, 则需要 N行M列的表.
//

#include <stdio.h>
#include <stdlib.h>
#include <vector>


#define MAX_MINES		5
#define MAX_WORKER		10

// 金矿信息
struct FGoldMineMeta
{
	int		Golds;  // 金量
	int		Workers;// 工人
};

// 表格项
struct FTableItem
{
	int		MaxGolds; //最大产出
	bool	bDig;	  // 是否挖此矿
};

int main()
{
	FGoldMineMeta  Mines[MAX_MINES] = {
		{ 400, 5},
		{ 500, 5},
		{ 200, 3},
		{ 300, 4},
		{ 350, 3}
	};

	FTableItem Table[MAX_MINES][MAX_WORKER];

	// F(1, M)
	for (int m = 1; m <= MAX_WORKER; m++)
	{
		FTableItem &Item = Table[0][m - 1];
		if (m < Mines[0].Workers)
		{
			Item.bDig = false;
			Item.MaxGolds = 0;
		}
		else
		{
			Item.bDig = true;
			Item.MaxGolds = Mines[0].Golds;
		}
	}

	// F(N, M) = max(F(N-1, M), F(N-1, M-W[N-1]) + G[N-1])
	for (int n = 1; n < MAX_MINES; n++)
	{
		for (int m = 1; m <= MAX_WORKER; m++)
		{
			FTableItem &Item = Table[n][m - 1];

			int Fa, Fb;
			Fa = Table[n - 1][m - 1].MaxGolds;
			Fb = 0;
			if (m >= Mines[n].Workers)
			{
				Fb = Mines[n].Golds;
				int RemainWorkers = m - Mines[n].Workers;
				if (RemainWorkers > 0)
				{
					Fb += Table[n - 1][RemainWorkers - 1].MaxGolds;
				}
			}

			if (Fa >= Fb)
			{
				Item.bDig = false;
				Item.MaxGolds = Fa;
			}
			else
			{
				Item.bDig = true;
				Item.MaxGolds = Fb;
			}
		}
	}


	// display result
	// F(5, 10)
	printf("动态规划 Max Dig Golds: %d\n", Table[MAX_MINES-1][MAX_WORKER-1].MaxGolds);
	printf("Solution: ");

	std::vector<int> MinesDig;
	for (int k = MAX_MINES - 1, w=MAX_WORKER; k >= 0; k--)
	{
		FTableItem &Item = Table[k][w-1];
		if (Item.bDig)
		{
			MinesDig.push_back(k);

			int RemainWorker = w - Mines[k].Workers;
			if (RemainWorker <= 0)
			{
				break;
			}

			w = RemainWorker;
		}
	}

	for (size_t k = MinesDig.size(); k > 0; k--)
	{
		printf("金矿%d  ", MinesDig[k-1]);
	}

	printf("\n");
	system("pause");
    return 0;
}