2023arXiv_A Fast and Lightweight Network for Low-Light Image Enhancement(FLW)

一. Motivtaion

低光图像增强目前的方法不能同时处理低亮度、低对比度、颜色失真

二.Contribution

1. 提出一个全局组件可以有效提高处理速度

2. 设计了几个新奇的损失函数

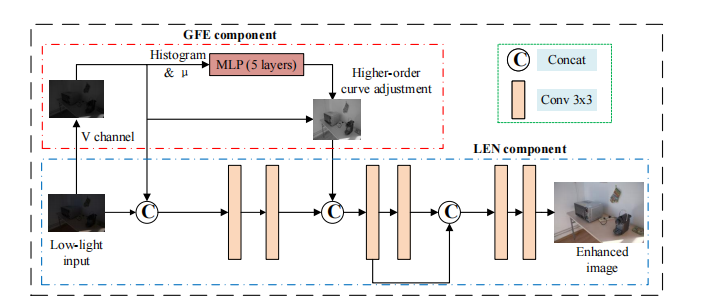
三. Network

 对应代码有点出入：

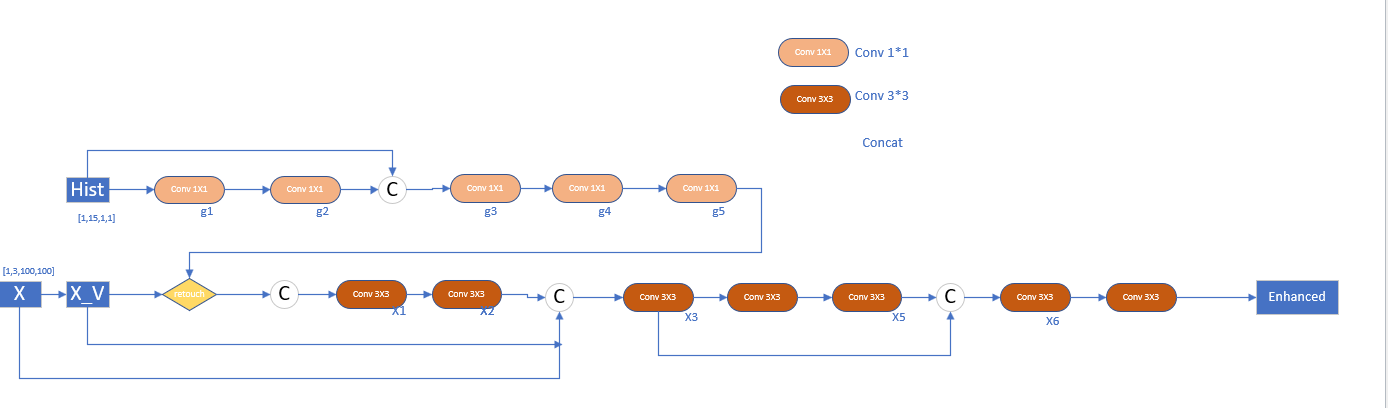
 网络结构解读：

GFE：

获取图像的HSV（Hue:色调，S饱和度，V亮度）中的V通道 ：即RGB值的最大值

low_im_filter_max = np.max(low, axis=2, keepdims=True)  # positive (H, W, 1)

对于输入低光照的图像PIL读入图像H W C获取V Channel（HSV）

进入直方图统计，统计在V通道中最大值到最小值的14个区间的值，对于hist[1,1,15]  第三维中位置前12设置为统计的直方图并归一化，位置13设置为低光图像V通道的最小值，位置14设置为低光图像V通道的最大值，位置15设置为正常光图像V通道的平均值，放入MLP中MLP是五个卷积操作，之后放入高阶曲线亮度调整函数（Zero_DCE提出）

LEN网络结构比较简单： 七个卷积加跳连接

四. Loss：

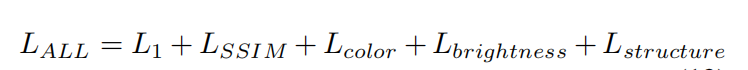
（1）L1损失：均方误差

L1 = torch.abs(R_low - high).mean()

 （2）Lssim损失：使用的是pytorch_ssim中自带的SSIM损失

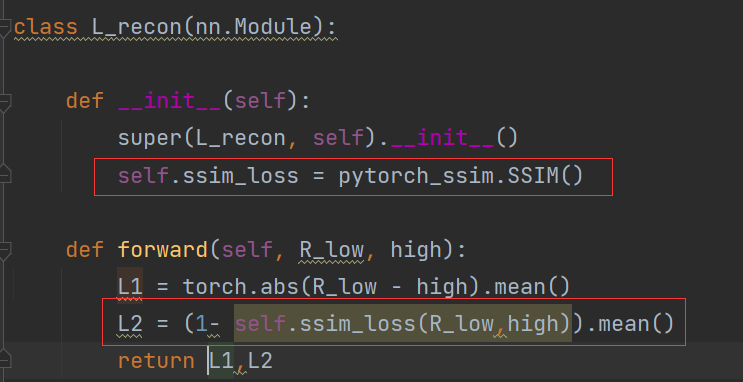
 （3）作者认为对图像低光增强之后颜色信息应该是能尽量保留的，亦即增强后图像与参考图像(监督图像)的色调和饱和度应该是正比例关系。使用余弦相似度度量增强前后图片的HSV，实际上就是在计算色调、饱和度的相关性。但是在代码实现中1-余弦相似度，但是由于两张图片很接近时，余弦相似度为1从而容易使得Lcolor变为0，容易使得梯度消失，所以在代码实现中最后的损失又加了一个反余弦的计算，避免梯度消失

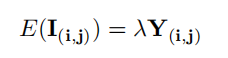
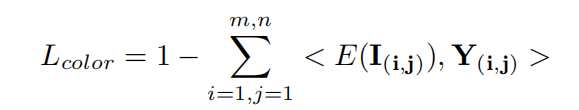
i,j 是像素坐标， E（I(i,j))是增强后的图像， Y（i,j）是GT

class L_color_zy(nn.Module):

    def __init__(self):
        super(L_color_zy, self).__init__()

    def forward(self, x, y):
        product_separte_color = (x * y).mean(1, keepdim=True)
        x_abs = (x ** 2).mean(1, keepdim=True) ** 0.5
        y_abs = (y ** 2).mean(1, keepdim=True) ** 0.5
        # torch.acos(x,out = None)计算按元素的反余弦值
        loss1 = (1 - product_separte_color / (x_abs * y_abs + 0.00001)).mean() + \
            torch.mean(torch.acos(product_separte_color / (x_abs * y_abs + 0.00001)))

        return loss1

（4）亮度损失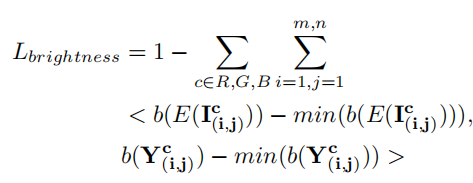：                 c指的是是r,g,b三通道。b(·)代表像素周围的块 。

按照作者原文的解释，也就是参考图像亮的部分增强图像也应该亮。这里对图像明暗程度的衡量并不是一个pixel-wise的概念，而是对每个像素周边的区域的余弦相似度计算。因为线性关系的两者之间可能存在一个常数的差值，因此在计算余弦相似度时需要减去各自区域的最小值(这也是为什么对明暗程度的衡量并不是一个pixel-wise的)。

class L_bright_cosist(nn.Module):

    def __init__(self):
        super(L_bright_cosist, self).__init__()

    def gradient_Consistency_loss_patch(self, x, y):
        # B*C*H*W
        #  torch.abs取绝对值; x.min()返回指定维度的最小数和对应下标,取[0]只取最小值
        # 该行代码的核心功能是计算一个张量沿着第 2 和第 3 维度的最小值，并对其进行取绝对值和截断操作（分离出来）。
        # 使用 detach() 方法将张量从计算图中分离出来，避免梯度回传对该张量产生影响。这种分离通常用于不需要梯度的张量，以节省内存并加速模型训练
        min_x = torch.abs(x.min(2, keepdim=True)[0].min(3, keepdim=True)[0]).detach()  # [1,3,1,1]
        min_y = torch.abs(y.min(2, keepdim=True)[0].min(3, keepdim=True)[0]).detach()
        x = x - min_x
        y = y - min_y
        # B*1*1,3
        # .mean([2, 3])按照高宽取平均值
        product_separte_color = (x * y).mean([2, 3], keepdim=True)
        x_abs = (x ** 2).mean([2, 3], keepdim=True) ** 0.5
        y_abs = (y ** 2).mean([2, 3], keepdim=True) ** 0.5
        loss1 = (1 - product_separte_color / (x_abs * y_abs + 0.00001)).mean() + torch.mean(
            torch.acos(product_separte_color / (x_abs * y_abs + 0.00001)))

        # 按照通道取平均值？
        product_combine_color = torch.mean(product_separte_color, 1, keepdim=True)
        # 通过沿着第 2 和第 3 维度求平均值，可以将 x 和 y 中每个通道的特征图压缩成一个标量，以减少特征图的维度并提取出有意义的统计信息。这种操作通常用于卷积神经网络（CNN）中的池化层或特征融合操作。
        x_abs2 = torch.mean(x_abs ** 2, 1, keepdim=True) ** 0.5
        y_abs2 = torch.mean(y_abs ** 2, 1, keepdim=True) ** 0.5
        loss2 = torch.mean(1 - product_combine_color / (x_abs2 * y_abs2 + 0.00001)) + torch.mean(
            torch.acos(product_combine_color / (x_abs2 * y_abs2 + 0.00001)))
        return loss1 + loss2

    def forward(self, x, y):
        B, C, H, W = x.shape
        loss = self.gradient_Consistency_loss_patch(x, y)
        # loss1 = 0
        # # 0:H // 2 高取0到H/2   H // 2: 高取H/2到H
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, 0:H // 2, 0:W // 2], y[:, :, 0:H // 2, 0:W // 2])
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, H // 2:, 0:W // 2], y[:, :, H // 2:, 0:W // 2])
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, 0:H // 2, W // 2:], y[:, :, 0:H // 2, W // 2:])
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, H // 2:, W // 2:], y[:, :, H // 2:, W // 2:])

        return loss  # +loss1#+torch.mean(torch.abs(x-y))#+loss1

（5）结构损失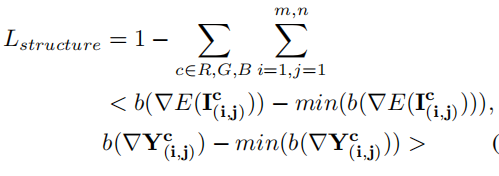：                     倒三角是一个梯度计算

图像的结构在增强前后不应该有改变，也就是内容应当尽量相似。在我们之前已经阅读过的文章中，结构损失也是可以用相关系数来描述的，但是此处作者使用每个像素处的梯度来衡量图像结构之间的差异。与明度相同，结构差异也应当是符合一个线性关系的，同样使用一次函数的公式来描述，也同样需要减去一个误差。

# 这段代码定义了一个名为"L_grad_cosist"的类，该类继承自PyTorch中的nn.Module，用于计算两张图像之间的梯度一致性损失。
# 在初始化函数__init__()中，该程序首先定义了两个卷积核kernel_right和kernel_down，这两个卷积核分别对应于求解水平方向和垂直方向的图像梯度。
# 然后利用这两个卷积核，分别构建了权重矩阵self.weight_right和self.weight_down，并将它们转换成nn.Parameter类型。
# 在梯度计算函数gradient_of_one_channel()中，程序利用了pytorch中的F.conv2d函数对x和y进行卷积操作，并分别计算了原始图像x和增强后的图像y在水平和垂直方向上的梯度。
# 最后，函数返回四个梯度张量值，分别对应于原始图像x在水平和垂直方向上的梯度，以及增强后的图像y在水平和垂直方向上的梯度。
class L_grad_cosist(nn.Module):

    def __init__(self):
        super(L_grad_cosist, self).__init__()
        kernel_right = torch.FloatTensor([[0, 0, 0], [0, 1, -1], [0, 0, 0]]).cuda().unsqueeze(0).unsqueeze(0)
        kernel_down = torch.FloatTensor([[0, 0, 0], [0, 1, 0], [0, -1, 0]]).cuda().unsqueeze(0).unsqueeze(0)
        self.weight_right = nn.Parameter(data=kernel_right, requires_grad=False)
        self.weight_down = nn.Parameter(data=kernel_down, requires_grad=False)

    def gradient_of_one_channel(self, x, y): # [1, H, W] R/G/B
        # conv2d 小写 函数卷积操作
        D_org_right = F.conv2d(x, self.weight_right, padding="same")
        D_org_down = F.conv2d(x, self.weight_down, padding="same")
        D_enhance_right = F.conv2d(y, self.weight_right, padding="same")
        D_enhance_down = F.conv2d(y, self.weight_down, padding="same")
        return torch.abs(D_org_right), torch.abs(D_enhance_right), torch.abs(D_org_down), torch.abs(D_enhance_down)

    def gradient_Consistency_loss_patch(self, x, y):
        # B*C*H*W
        min_x = torch.abs(x.min(2, keepdim=True)[0].min(3, keepdim=True)[0]).detach()
        min_y = torch.abs(y.min(2, keepdim=True)[0].min(3, keepdim=True)[0]).detach()
        x = x - min_x
        y = y - min_y
        # B*1*1,3
        product_separte_color = (x * y).mean([2, 3], keepdim=True)
        x_abs = (x ** 2).mean([2, 3], keepdim=True) ** 0.5
        y_abs = (y ** 2).mean([2, 3], keepdim=True) ** 0.5
        loss1 = (1 - product_separte_color / (x_abs * y_abs + 0.00001)).mean() + torch.mean(
            torch.acos(product_separte_color / (x_abs * y_abs + 0.00001)))

        product_combine_color = torch.mean(product_separte_color, 1, keepdim=True)
        x_abs2 = torch.mean(x_abs ** 2, 1, keepdim=True) ** 0.5
        y_abs2 = torch.mean(y_abs ** 2, 1, keepdim=True) ** 0.5
        loss2 = torch.mean(1 - product_combine_color / (x_abs2 * y_abs2 + 0.00001)) + torch.mean(
            torch.acos(product_combine_color / (x_abs2 * y_abs2 + 0.00001)))
        return loss1 + loss2

    def forward(self, x, y):
        # x[:, 0:1, :, :] 取第一个通道
        x_R1, y_R1, x_R2, y_R2 = self.gradient_of_one_channel(x[:, 0:1, :, :], y[:, 0:1, :, :])
        x_G1, y_G1, x_G2, y_G2 = self.gradient_of_one_channel(x[:, 1:2, :, :], y[:, 1:2, :, :])
        x_B1, y_B1, x_B2, y_B2 = self.gradient_of_one_channel(x[:, 2:3, :, :], y[:, 2:3, :, :])
        x = torch.cat([x_R1, x_G1, x_B1, x_R2, x_G2, x_B2], 1)
        y = torch.cat([y_R1, y_G1, y_B1, y_R2, y_G2, y_B2], 1)

        B, C, H, W = x.shape
        loss = self.gradient_Consistency_loss_patch(x, y)
        # loss1 = 0
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, 0:H // 2, 0:W // 2], y[:, :, 0:H // 2, 0:W // 2])
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, H // 2:, 0:W // 2], y[:, :, H // 2:, 0:W // 2])
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, 0:H // 2, W // 2:], y[:, :, 0:H // 2, W // 2:])
        # loss1 += self.gradient_Consistency_loss_patch(x[:, :, H // 2:, W // 2:], y[:, :, H // 2:, W // 2:])

        return loss  # +loss1#+torch.mean(torch.abs(x-y))#+loss1

 

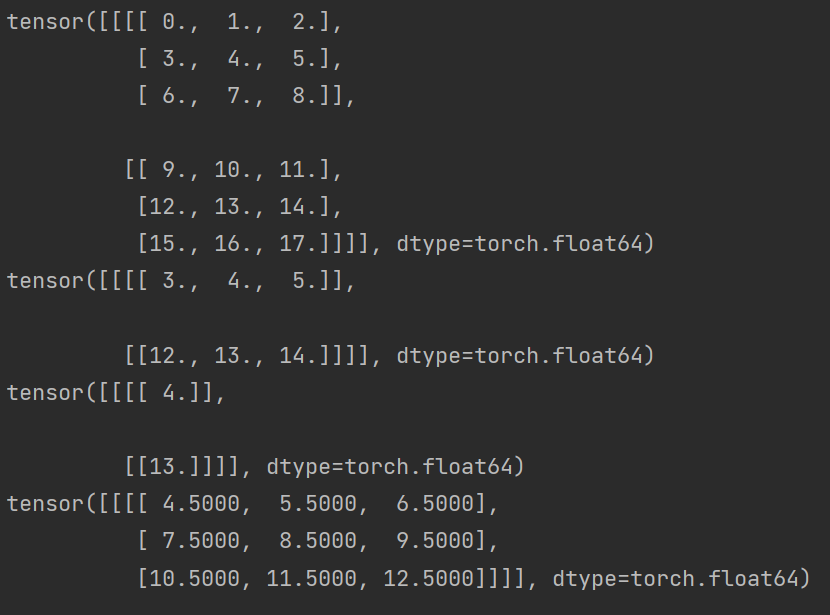
x_abs = (x ** 2).mean([2, 3], keepdim=True) ** 0.5和

 mean的解释代码：

x = torch.arange(18,dtype=float).reshape(1, 2, 3, 3)
print(x)
y = x.mean([2],keepdim=True)
print(y)
x_abs = x.mean([2,3],keepdim=True)
x_abs2 = torch.mean(x ,1, keepdim=True)
print(x_abs)
print(x_abs2)