浅谈Tarjan算法
预备知识
设无向图$G_{0} = (V_{0}, E_{0})$,其中$V_{0}$为定点集合,$E_{0}$为边集,设有向图$G_{1} = (V_{1}, E_{1})$,其中$V_{1}$为定点集合,$E_{1}$为边集。
- 无向图中的路径:如果存在一个顶点序列$v_{p},v_{i_{1}},\cdots,v_{i_{k}},v_{q}$,使得$\left ( v_{p}, v_{i_{1}} \right ),\left ( v_{i_{1}},v_{i_{2}} \right ),\cdots,\left ( v_{k-1}, v_{k} \right ),\left ( v_{k}, v_{q} \right )\in E_{0}$,那么称$v_{p}$到$v_{q}$之间存在一条路径。
- 有向图中的路径:如果存在一个顶点序列$v_{p},v_{i_{1}},\cdots,v_{i_{k}},v_{q}$,使得$\left ( v_{p}, v_{i_{1}} \right ),\left ( v_{i_{1}},v_{i_{2}} \right ),\cdots,\left ( v_{k-1}, v_{k} \right ),\left ( v_{k}, v_{q} \right )\in E_{1}$,那么称$v_{p}$到$v_{q}$之间存在一条路径。
- 连通图:在无向图中,对于任意有序对$\left ( v_{i},v_{j} \right )\in(V_{0}\times V_{0})$,都存在一条$v_{i}$到$v_{j}$的路径。
- 强连通图:在有向图中,对于任意有序对$\left ( v_{i},v_{j} \right )\in(V_{1}\times V_{1})$,都存在一条$v_{i}$到$v_{j}$的路径。
- 连通分量:无向图$G$的极大连通子图是$G$的连通分量。
- 强连通分量:有向图$G$的极大强连通子图是$G$的强连通分量。
- 割点:在无向图$G$中,如果存在点$v_{0}$满足删除它后,新图的连通分量的个数增加,那么$v_{0}$为原图的一个割点。
- 割边(又称为桥):在无向图$G$中,如果存在边$e_{0}$满足删除它后,新图的连通分量的个数增加,那么$e_{0}$为原图的一条割边。
- 边-双连通图:若无向连通图$G$中不存在割边,则无向图$G$是边-双连通图
- 点-双连通图:若无向连通图$G$中不存在割点,则无向图$G$是点-双连通图
- 点-双连通分量:无向图$G$中的极大点-双连通子图是它的点-双连通分量
- 边-双连通分量:无向图$G$中的极大边-双连通子图是它的边-双连通分量
两个数组
$dfn_i$:点$i$的深度优先数(英文可能是Depth First Number),可以理解为是第几个被搜索到的节点。
$low_i$:在点$i$的dfs子树中通过1条返祖边到达的最早祖先。
Tarjan算法首先会对原图进行深度优先搜索。
当从一个访问过的点通过边$e$到达一个未访问的点,则将边$e$标记为树边。如果一条非树边$(u, v)$使得要么$u$是$v$的祖先满足,要么$v$是$u$的祖先,那么称边$(u, v)$是一条返祖边。
显然当遇到一条返祖边时,需要用它来更新当前点的$low$值
通过Tarjan算法得到的生成森林是dfs生成森林:
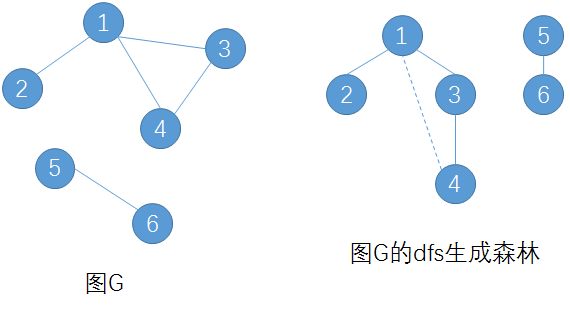
(其中虚边是返祖边)
Tarjan算法的应用
求割点和割边
首先给出一个结论
定理1 无向图中的每一条边,要么是树边,要么是返祖边。
证明 假如存在其他边,它满足它不连它的祖先也不连它的后代,那么它一定是满足:
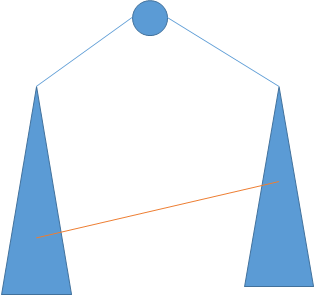
然后根据dfs的性质和无向边的性质,容易得到不存在这种情况。
假如现在考虑点$p$是不是割点,分两种情况讨论:
- 如果$p$是树根,那么只要$p$的子节点个数大于1,那么$p$就是割点。因为$p$不存在祖先,点$p$的不同子树中的两点之间的路径必须经过点1(因为根节点的位于它不同子树内的两点的LCA是根节点,然后根据定理1得到,从其中一个点开始走,经过的每一条边要么到它的后代要么到它的祖先,所以必定经过1)。
- 如果$p$不是树根,那么只要存在一个子节点$x$满足$low_x \geqslant dfn_p$,那么点$p$是割点。因为假如点$p$被删掉后,点$x$无法到达$p$的祖先,而这之前是可以到达的,所以连通分量的个数至少增加了1.
Code

1 /** 2 * poj 3 * Problem#1144 4 * Accepted 5 * Time: 16ms 6 * Memory: 672k 7 */ 8 #include <algorithm> 9 #include <iostream> 10 #include <cstring> 11 #include <cstdio> 12 #include <vector> 13 using namespace std; 14 typedef bool boolean; 15 16 const int N = 105; 17 18 int n; 19 int cnt, res; 20 int dfn[N], low[N]; 21 boolean vis[N]; 22 vector<int> g[N]; 23 24 inline boolean init() { 25 scanf("%d", &n); 26 if (!n) return false; 27 for (int i = 1; i <= n; i++) 28 g[i].clear(); 29 int u, v; 30 while (~scanf("%d", &u) && u) { 31 while (getchar() != '\n') { 32 scanf("%d", &v); 33 g[u].push_back(v); 34 g[v].push_back(u); 35 } 36 } 37 return true; 38 } 39 40 void tarjan(int p, int fa) { 41 int cson = 0; 42 dfn[p] = low[p] = ++cnt; 43 vis[p] = true; 44 for (int i = 0; i < (signed)g[p].size(); i++) { 45 int e = g[p][i]; 46 if (e == fa) continue; 47 if (!vis[e]) { 48 tarjan(e, p); 49 low[p] = min(low[p], low[e]); 50 if (low[e] >= dfn[p]) 51 cson++; 52 } else 53 low[p] = min(low[p], dfn[e]); 54 } 55 if ((!fa && cson > 1) || (fa && cson)) 56 res++; 57 } 58 59 inline void solve() { 60 cnt = 0, res = 0; 61 memset(vis, false, sizeof(boolean) * (n + 1)); 62 for (int i = 1; i <= n; i++) 63 if (!vis[i]) 64 tarjan(i, 0); 65 printf("%d\n", res); 66 } 67 68 int main() { 69 while (init()) { 70 solve(); 71 } 72 return 0; 73 }
求桥的话,相对就简单一些。
一个非常显然的结论:
定理2 返祖边不可能是桥。
证明 因为返祖边的两端一定通过树边连通。所以删掉返祖边不会改变图的连通性。
因此割边的个数不会超过$n - 1$(一个显然,但没多大用的性质)。
我更想说的是,再根据定理1可以得到桥一定是树边。
考虑什么样的树边被断掉后图的连通分量的个数增加。假如这条树边两端的点是$u, v$,其中$u$是$v$的爸爸父节点。删掉边$(u, v)$后,连通分量个数增加的充分必要条件是$v$无法通过返祖边到达$u$或者$u$的祖先。因此,不难得到条件是$low_v = dfn_v$。
Code

1 /** 2 * hdu 3 * Problem#4738 4 * Accepted 5 * Time: 187ms 6 * Memory: 25264k 7 */ 8 #include <iostream> 9 #include <cstring> 10 #include <cstdio> 11 using namespace std; 12 typedef bool boolean; 13 14 const int N = 1005, M = 2e6 + 5; 15 16 typedef class Edge { 17 public: 18 int end; 19 int next; 20 int w; 21 22 Edge(int end = 0, int next = 0, int w = 0):end(end), next(next), w(w) { } 23 }Edge; 24 25 typedef class MapManager { 26 public: 27 int ce; 28 int h[N]; 29 Edge es[M]; 30 31 void addEdge(int u, int v, int w) { 32 es[++ce] = Edge(v, h[u], w); 33 h[u] = ce; 34 } 35 36 void addDoubleEdge(int u, int v, int w) { 37 addEdge(u, v, w); 38 addEdge(v, u, w); 39 } 40 41 Edge& operator [] (int p) { 42 return es[p]; 43 } 44 }MapManager; 45 46 int n, m; 47 int cnt, res; 48 int dfn[N], low[N]; 49 boolean vis[N]; 50 MapManager g; 51 52 inline boolean init() { 53 scanf("%d%d", &n, &m); 54 if (!n && !m) 55 return false; 56 g.ce = -1; 57 memset(g.h, -1, sizeof(int) * (n + 1)); 58 for (int i = 1, u, v, w; i <= m; i++) { 59 scanf("%d%d%d", &u, &v, &w); 60 g.addDoubleEdge(u, v, w); 61 } 62 return true; 63 } 64 65 void tarjan(int p, int laste) { 66 dfn[p] = low[p] = ++cnt; 67 vis[p] = true; 68 for (int i = g.h[p]; ~i; i = g[i].next) { 69 int e = g[i].end, w = g[i].w; 70 if (i == laste) continue; 71 if (!vis[e]) { 72 tarjan(e, i ^ 1); 73 low[p] = min(low[p], low[e]); 74 if (low[e] == dfn[e]) 75 res = min(res, w); 76 } else 77 low[p] = min(low[p], dfn[e]); 78 } 79 } 80 81 inline void solve() { 82 cnt = 0, res = 211985; 83 memset(vis, false, sizeof(boolean) * (n + 1)); 84 tarjan(1, -1); 85 if (!res) res = 1; // 坑.... 86 for (int i = 2; i <= n; i++) 87 if (!vis[i]) { 88 res = 0; 89 break; 90 } 91 if (res == 211985) res = -1; 92 printf("%d\n", res); 93 } 94 95 int main() { 96 while (init()) 97 solve(); 98 return 0; 99 }
求点-双连通分量
在求点-双连通分量(以下简称为点双)之前,我们再来证明一个东西:
定理3 每条边恰好属于一个点双。
证明 首先来说明每条边一定属于一个点双连通子图。考虑这条边的两个端点以及它本身构成的子图,显然它是点双连通的。
然后来说明任意两个点双没有公共边。
假设存在两个点双有一条公共边$(u, v)$,假设它们的点集分别为$V_1, V_2$。如果删掉的点$x\in V_1$或$x\in V_2$,且$x\neq u, x\neq v$,根据点双的定义容易得到新图的连通性不会改变。如果删掉的点是$u$,那么剩余的点一定与$v$连通,所以它仍然不会改变图的连通性。对于如果删掉的点是$v$同理可证不会改变新图的连通性。所以删掉$V_1 \cup V_2$中任意一个点都不会改变图的连通性。因此它们能够组成更大的一个点双连通子图,与点双的定义矛盾。
由这个证明过程不难得到点双的点集大小至少为2,所以在考虑找到所有点双的时候可以考虑边。
定理4 每个点双包含至少一条树边。
证明 假设存在一个点双不包含任意一条树边。我们考虑从这个点双中选取2个不同点$u, v$,它们在dfs生成树上存在唯一一条路径。我们把它加入这个点双中,如果删掉非路径上的点,那么剩余点与$u, v$连通。如果删掉的是$u$或者$v$,那么剩下点会与另外一个点连通。如果删掉的是路径上的一个点(不含端点),那么路径上一部分点会与$u$连通,另一部分与$v$,$u, v$和原点双中的点一定连通。所以新子图还是一个点双连通子图,与点双的定义矛盾。
所以点双的数量不会超过$n - 1$。
我们考虑在回溯的时候找到一个点双。
考虑判断一条树边是不是一个点双内的树边中深度最低的一条边。假设它深度较深的一端是$v$,较浅的一端是$u$。那么当$v$无法连向$u$的祖先的时候,加入$u$后再加入另一条与$u$连通的树边,那么删掉$u$后就会多产生连通块,所以当$low_v \geqslant dfn_u$的时候,这条边是这个点双内的最后一条边。
如果需要求出点双内的所有点和所有边可以用一个栈记录一下边。
注意一下返祖边只在子节点的时候加入,这个可以通过判断深度优先数的大小解决掉(你一定也不希望在其他某个点双内莫名其妙多出一条边)。
Code

1 /** 2 * poj 3 * Problem#2942 4 * Accepted 5 * Time: 1063ms 6 * Memory: 1128k 7 */ 8 #include <iostream> 9 #include <cstdlib> 10 #include <cstdio> 11 #include <vector> 12 #include <stack> 13 using namespace std; 14 typedef bool boolean; 15 16 template <typename T> 17 void pfill(T* pst, const T* ped, T val) { 18 for ( ; pst != ped; *(pst++) = val); 19 } 20 21 const int N = 1e3 + 3, M = (N * N) << 1; 22 23 typedef class Edge { 24 public: 25 int ed, nx; 26 27 Edge(int ed = 0, int nx = 0):ed(ed), nx(nx) { } 28 }Edge; 29 30 typedef class MapManager { 31 public: 32 int h[N]; 33 vector<Edge> es; 34 35 void addEdge(int u, int v) { 36 es.push_back(Edge(v, h[u])); 37 h[u] = (signed) es.size() - 1; 38 } 39 40 Edge& operator [] (int p) { 41 return es[p]; 42 } 43 }MapManager; 44 45 #define pii pair<int, int> 46 47 int n, m; 48 int col[N]; 49 stack<pii> s; 50 MapManager g; 51 int dfs_clock; 52 boolean res[N]; 53 MapManager subg; 54 boolean rg[N][N]; 55 int dfn[N], low[N]; 56 vector<int> bpoints; 57 58 inline boolean init() { 59 scanf("%d%d", &n, &m); 60 if (!n && !m) 61 return false; 62 g.es.clear(); 63 dfs_clock = 0; 64 pfill(dfn, dfn + n + 1, 0); 65 pfill(col, col + n + 1, -1); 66 pfill(g.h, g.h + n + 1, -1); 67 pfill(res, res + n + 1, false); 68 pfill(subg.h, subg.h + n + 1, -1); 69 for (int i = 1; i <= n; i++) 70 for (int j = 1; j <= n; j++) 71 rg[i][j] = false; 72 for (int i = 1, u, v; i <= m; i++) { 73 scanf("%d%d", &u, &v); 74 rg[u][v] = rg[v][u] = true; 75 } 76 return true; 77 } 78 79 boolean color(int p, int c) { 80 if (~col[p]) 81 return col[p] == c; 82 col[p] = c; 83 for (int i = subg.h[p]; ~i; i = subg[i].nx) 84 if (!color(subg[i].ed, col[p] ^ 1)) 85 return false; 86 return true; 87 } 88 89 void dispose() { 90 if (!color(bpoints[0], 0)) { 91 for (unsigned i = 0; i < bpoints.size(); i++) 92 res[bpoints[i]] = true; 93 } 94 for (unsigned i = 0; i < bpoints.size(); i++) 95 subg.h[bpoints[i]] = -1, col[bpoints[i]] = -1; 96 subg.es.clear(); 97 bpoints.clear(); 98 } 99 100 void tarjan(int p, int last_edge) { 101 dfn[p] = low[p] = ++dfs_clock; 102 103 pii now, cur; 104 for (int i = g.h[p], e; ~i; i = g[i].nx) { 105 e = g[i].ed; 106 if (i == (last_edge ^ 1)) 107 continue; 108 now = pii(min(p, e), max(p, e)); 109 if (!dfn[e]) { 110 s.push(now); 111 tarjan(e, i); 112 low[p] = min(low[p], low[e]); 113 if (low[e] >= dfn[p]) { 114 do { 115 cur = s.top(); 116 s.pop(); 117 subg.addEdge(cur.first, cur.second); 118 subg.addEdge(cur.second, cur.first); 119 bpoints.push_back(cur.first); 120 bpoints.push_back(cur.second); 121 } while (now != cur); 122 dispose(); 123 } 124 } else { 125 low[p] = min(low[p], dfn[e]); 126 if (dfn[e] < dfn[p]) 127 s.push(pii(min(p, e), max(p, e))); 128 } 129 } 130 } 131 132 inline void solve() { 133 for (int i = 1; i <= n; i++) 134 for (int j = i + 1; j <= n; j++) 135 if (!rg[i][j]) { 136 g.addEdge(i, j); 137 g.addEdge(j, i); 138 } 139 140 for (int i = 1; i <= n; i++) 141 if (!dfn[i]) 142 tarjan(i, -1); 143 144 int answer = 0; 145 for (int i = 1; i <= n; i++) 146 answer += !res[i]; 147 printf("%d\n", answer); 148 } 149 150 int main() { 151 while (init()) 152 solve(); 153 return 0; 154 }
有时候我们希望求出点双内的点,这个时候栈内记录边略显得麻烦,可以考虑找到一个点的时候加入一个点,它在找到包含它到它的父节点的那条树边的点双时被弹出栈。具体细节可以见代码。
Code
/**
* loj
* Problem#2562
* Accepted
* Time: 2431ms
* Memory: 21964k
*/
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
const int N = 1e5 + 5, N2 = N << 1;
template <typename T>
void pfill(T* pst, const T* ped, T val) {
for ( ; pst != ped; *(pst++) = val);
}
typedef class Edge {
public:
int ed, nx;
Edge() { }
Edge(int ed, int nx) : ed(ed), nx(nx) { }
} Edge;
typedef class MapManager {
public:
int h[N << 1];
vector<Edge> es;
void init(int n) {
pfill(h + 1, h + n + 1, -1);
es.clear();
}
void add_edge(int u, int v) {
es.emplace_back(v, h[u]);
h[u] = (signed) es.size() - 1;
}
Edge& operator [] (int p) {
return es[p];
}
} MapManager;
int Case;
int n, m;
MapManager G, Tr;
int cnt_node, dfs_clock;
int value[N2];
inline void init() {
scanf("%d%d", &n, &m);
G.init(n);
Tr.init(n << 1);
cnt_node = n;
pfill(value + 1, value + n + 1, 1);
for (int i = 1, u, v; i <= m; i++) {
scanf("%d%d", &u, &v);
G.add_edge(u, v);
G.add_edge(v, u);
}
}
stack<int> S;
boolean vis[N];
int dfn[N], low[N];
void init_tarjan() {
dfs_clock = 0;
while (!S.empty()) S.pop();
pfill(vis + 1, vis + n + 1, false);
}
void Tarjan(int p) {
S.push(p);
vis[p] = true;
dfn[p] = low[p] = ++dfs_clock;
for (int i = G.h[p], e; ~i; i = G[i].nx) {
e = G[i].ed;
if (!vis[e]) {
Tarjan(e);
low[p] = min(low[p], low[e]);
if (low[e] >= dfn[p]) {
int now = -1, id = ++cnt_node;
value[id] = 0;
do {
now = S.top();
S.pop();
Tr.add_edge(id, now);
Tr.add_edge(now, id);
} while (now != e);
Tr.add_edge(id, p);
Tr.add_edge(p, id);
}
} else {
low[p] = min(low[p], dfn[e]);
}
}
}
int sz[N2], zson[N2], dep[N2];
int in[N2], top[N2], fa[N2];
void dfs1(int p, int Fa) {
int mx = -1, &id = zson[p];
sz[p] = 1, fa[p] = Fa;
value[p] += value[Fa], dep[p] = dep[Fa] + 1, id = -1;
for (int i = Tr.h[p], e; ~i; i = Tr[i].nx) {
e = Tr[i].ed;
if (e ^ Fa) {
dfs1(e, p);
sz[p] += sz[e];
if (sz[e] > mx) {
mx = sz[e];
id = e;
}
}
}
}
void dfs2(int p, boolean ontop) {
in[p] = ++dfs_clock;
top[p] = (!ontop) ? (top[fa[p]]) : (p);
if (~zson[p]) {
dfs2(zson[p], false);
}
for (int i = Tr.h[p], e; ~i; i = Tr[i].nx) {
e = Tr[i].ed;
if (e != fa[p] && e != zson[p]) {
dfs2(e, p);
}
}
}
int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) {
swap(u, v);
}
u = fa[top[u]];
}
return (dep[u] < dep[v]) ? (u) : (v);
}
inline void solve() {
static int S[N2];
init_tarjan();
Tarjan(1);
dfs_clock = 0;
dfs1(1, 0);
dfs2(1, true);
int Q, K;
scanf("%d", &Q);
while (Q--) {
scanf("%d", &K);
for (int i = 1; i <= K; i++) {
scanf("%d", S + i);
}
sort(S + 1, S + K + 1, [&] (const int& u, const int& v) {
return in[u] < in[v];
});
int vd = value[fa[lca(S[1], S[K])]];
int ans = value[S[1]] - vd, g;
for (int i = 1; i < K; i++) {
g = lca(S[i], S[i + 1]);
ans += value[S[i + 1]] - value[g];
}
printf("%d\n", ans - K);
}
}
int main() {
scanf("%d", &Case);
while (Case--) {
init();
solve();
}
return 0;
}
求边-双连通分量
(下面将边-双连通分量简写为边双)
和点双类似,只不过这次我们考虑顶点:
定理5 每个顶点恰好属于一个边双。
证明 首先一个点的图是边双。
假设存在两个边双存在一个公共点$x$,那么删掉一条边都不会改变$x$和剩下的点的连通性。
我们考虑一个点是不是边双中的最浅的一个点。如果$dfn_p = low_p$,那么再加入它的某个父节点,那么它将成为割点。
如果需要求出边双内的所有点再用一个栈记录一下点就好了。
似乎还有一种做法是边双内一定不包含原图的桥,因此我们找到所有的桥,把它们删掉就得到了所有边双了。这个条件只是必要性,它的充分性可以考虑如果它删掉后使得连通块个数增加,那么它一定是原图的桥。(它是原图的一个子图,那么再加入若干端点都在它内部边后不会使得它的边连通性降低)。
Code

1 /** 2 * poj 3 * Problem#3177 4 * Accepted 5 * Time: 47ms 6 * Memory: 744k 7 */ 8 #include <iostream> 9 #include <cstdlib> 10 #include <cstdio> 11 #include <vector> 12 #include <stack> 13 using namespace std; 14 typedef bool boolean; 15 16 template <typename T> 17 void pfill(T* pst, const T* ped, T val) { 18 for ( ; pst != ped; *(pst++) = val); 19 } 20 21 const int N = 5e3 + 3, M = N << 1; 22 23 typedef class Edge { 24 public: 25 int ed, nx; 26 27 Edge(int ed = 0, int nx = 0):ed(ed), nx(nx) { } 28 }Edge; 29 30 typedef class MapManager { 31 public: 32 int* h; 33 vector<Edge> es; 34 35 MapManager() { } 36 MapManager(int n) { 37 h = new int[(n + 1)]; 38 pfill(h + 1, h + n + 1, -1); 39 } 40 41 void addEdge(int u, int v) { 42 es.push_back(Edge(v, h[u])); 43 h[u] = (signed) es.size() - 1; 44 } 45 46 Edge& operator [] (int p) { 47 return es[p]; 48 } 49 }MapManager; 50 51 int n, m; 52 int deg[N]; 53 MapManager g; 54 stack<int> s; 55 int dfs_clock; 56 int dfn[N], low[N]; 57 pair<int, int> es[M]; 58 59 inline void init() { 60 scanf("%d%d", &n, &m); 61 g = MapManager(n); 62 for (int i = 1, u, v; i <= m; i++) { 63 scanf("%d%d", &u, &v); 64 g.addEdge(u, v); 65 g.addEdge(v, u); 66 es[i] = pair<int, int>(u, v); 67 } 68 } 69 70 void tarjan(int p, int last_edge) { 71 dfn[p] = low[p] = ++dfs_clock; 72 s.push(p); 73 for (int i = g.h[p], e; ~i; i = g[i].nx) { 74 e = g[i].ed; 75 if (i == (last_edge ^ 1)) 76 continue; 77 if (!dfn[e]) { 78 tarjan(e, i); 79 low[p] = min(low[p], low[e]); 80 } else 81 low[p] = min(low[p], dfn[e]); 82 } 83 84 if (low[p] == dfn[p]) { 85 int cur; 86 do { 87 cur = s.top(); 88 s.pop(); 89 low[cur] = low[p]; 90 } while (cur != p); 91 } 92 } 93 94 inline void solve() { 95 for (int i = 1; i <= n; i++) 96 if (!dfn[i]) 97 tarjan(i, -1); 98 for (int i = 1; i <= m; i++) { 99 int u = es[i].first, v = es[i].second; 100 if (low[u] != low[v]) 101 deg[low[u]]++, deg[low[v]]++; 102 } 103 104 int cnt_leaf = 0; 105 for (int i = 1; i <= n; i++) 106 if (dfn[i] == low[i] && deg[low[i]] == 1) 107 cnt_leaf++; 108 printf("%d\n", (cnt_leaf + 1) >> 1); 109 } 110 111 int main() { 112 init(); 113 solve(); 114 return 0; 115 }
求强连通分量
有向图稍微要麻烦一点,不过基本思想还是一样的。
仍然考虑有向图的dfs生成森林,$dfn$数组以及$low$数组。
但是有向图中生成森林会复杂许多:
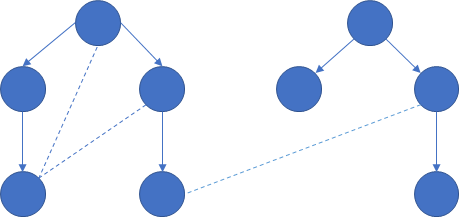
在更新$low$的时候要注意两个点是否在同一个子树内。
不难注意到一个强连通分量一定是某一个dfs子树内,所以我们仍然考虑一个强连通分量内的最浅点。
不难得到它的充分必要条件时$dfn_u = low_u$。必要性是因为,如果它能够到达它的若干级祖先,那么这一条链再加上这一条返祖边就能得到一个强连通子图,充分性显然,因为它自己就能构成一个强连通子图。
我们用类似于求边双的方法,就可以求出每个强连通分量内的所有点。

1 /** 2 * hdu 3 * Problem#1269 4 * Accepted 5 * Time: 46ms 6 * Memory: 3944k 7 */ 8 #include <iostream> 9 #include <cstdlib> 10 #include <cstdio> 11 #include <vector> 12 #include <stack> 13 using namespace std; 14 typedef bool boolean; 15 16 template <typename T> 17 void pfill(T* pst, const T* ped, T val) { 18 for ( ; pst != ped; *(pst++) = val); 19 } 20 21 const int N = 1e4 + 5; 22 23 typedef class Edge { 24 public: 25 int ed, nx; 26 27 Edge(int ed = 0, int nx = 0):ed(ed), nx(nx) { } 28 }Edge; 29 30 typedef class MapManager { 31 public: 32 int h[N]; 33 vector<Edge> es; 34 35 void addEdge(int u, int v) { 36 es.push_back(Edge(v, h[u])); 37 h[u] = (signed) es.size() - 1; 38 } 39 40 Edge& operator [] (int p) { 41 return es[p]; 42 } 43 }MapManager; 44 45 #define pii pair<int, int> 46 47 int n, m; 48 MapManager g; 49 stack<int> s; 50 int dfs_clock; 51 int dfn[N], low[N]; 52 boolean instack[N]; 53 54 inline boolean init() { 55 scanf("%d%d", &n, &m); 56 if (!n && !m) 57 return false; 58 g.es.clear(); 59 dfs_clock = 0; 60 pfill(dfn, dfn + n + 1, 0); 61 pfill(g.h, g.h + n + 1, -1); 62 for (int i = 1, u, v; i <= m; i++) { 63 scanf("%d%d", &u, &v); 64 g.addEdge(u, v); 65 } 66 return true; 67 } 68 69 int cnt_scc = 0; 70 void tarjan(int p) { 71 dfn[p] = low[p] = ++dfs_clock; 72 instack[p] = true; 73 s.push(p); 74 for (int i = g.h[p], e; ~i; i = g[i].nx) { 75 e = g[i].ed; 76 if (!dfn[e]) { 77 tarjan(e); 78 low[p] = min(low[e], low[p]); 79 } else if (instack[e]) 80 low[p] = min(dfn[e], low[p]); 81 } 82 83 if (low[p] == dfn[p]) { 84 int cur; 85 do { 86 cur = s.top(); 87 s.pop(); 88 instack[cur] = false; 89 } while (cur != p); 90 cnt_scc++; 91 } 92 } 93 94 inline void solve() { 95 cnt_scc = 0; 96 for (int i = 1; i <= n; i++) 97 if (!dfn[i]) 98 tarjan(i); 99 puts((cnt_scc == 1) ? ("Yes") : ("No")); 100 } 101 102 int main() { 103 while (init()) 104 solve(); 105 return 0; 106 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号