Codeforces 375C Circling Round Treasures - 最短路 - 射线法 - 位运算

 You have a map as a rectangle table. Each cell of the table is either an obstacle, or a treasure with a certain price, or a bomb, or an empty cell. Your initial position is also given to you.

You can go from one cell of the map to a side-adjacent one. At that, you are not allowed to go beyond the borders of the map, enter the cells with treasures, obstacles and bombs. To pick the treasures, you need to build a closed path (starting and ending in the starting cell). The closed path mustn't contain any cells with bombs inside. Let's assume that the sum of the treasures' values that are located inside the closed path equals v, and besides, you've made k single moves (from one cell to another) while you were going through the path, then such path brings you the profit of v - k rubles.

Your task is to build a closed path that doesn't contain any bombs and brings maximum profit.

Note that the path can have self-intersections. In order to determine if a cell lies inside a path or not, use the following algorithm:

  1. Assume that the table cells are points on the plane (the table cell on the intersection of the i-th column and the j-th row is point(i, j)). And the given path is a closed polyline that goes through these points.
  2. You need to find out if the point p of the table that is not crossed by the polyline lies inside the polyline.
  3. Let's draw a ray that starts from point p and does not intersect other points of the table (such ray must exist).
  4. Let's count the number of segments of the polyline that intersect the painted ray. If this number is odd, we assume that point p (and consequently, the table cell) lie inside the polyline (path). Otherwise, we assume that it lies outside.
Input

The first line contains two integers n and m (1 ≤ n, m ≤ 20) — the sizes of the table. Next n lines each contains m characters — the description of the table. The description means the following:

  • character "B" is a cell with a bomb;
  • character "S" is the starting cell, you can assume that it's empty;
  • digit c (1-8) is treasure with index c;
  • character "." is an empty cell;
  • character "#" is an obstacle.

Assume that the map has t treasures. Next t lines contain the prices of the treasures. The i-th line contains the price of the treasure with index i, vi ( - 200 ≤ vi ≤ 200). It is guaranteed that the treasures are numbered from 1 to t. It is guaranteed that the map has not more than 8 objects in total. Objects are bombs and treasures. It is guaranteed that the map has exactly one character "S".

Output

Print a single integer — the maximum possible profit you can get.

Examples
input
4 4
....
.S1.
....
....
10
output
2
input
7 7
.......
.1###2.
.#...#.
.#.B.#.
.3...4.
..##...
......S
100
100
100
100
output
364
input
7 8
........
........
....1B..
.S......
....2...
3.......
........
100
-100
100
output
0
input
1 1
S
output
0
Note

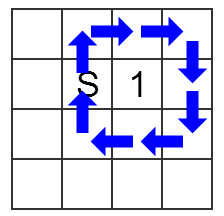
In the first example the answer will look as follows.

In the second example the answer will look as follows.

In the third example you cannot get profit.

In the fourth example you cannot get profit as you cannot construct a closed path with more than one cell.

题目大意

　　要求在网格图中，从指定点出发，走出一条回路（可以自交，有重边），不穿过任何一个物品（炸弹、障碍或者宝藏），使得围出来的图形不包含任何一个Bomb，并且最大化围住的宝藏的价值和减去走的步数。

判断一个点是否在多边形内的算法（射线法）

  1. 以这一点为端点，作出一条不穿过多边形任何一个顶点的射线
  2. 数与多边形的交点个数
  3. 如果交点个数为奇数，则这一点在多边形内，否则在多边形外

　　考虑增加一维k，把从每个物品引出向上的一条射线与路径的交点数的奇偶性用二进制压位。即$f[i][j][k]$表示当前在点$(i, j)$，状态为k的最短路径长度。

　　如何转移？这是个好问题。考虑穿过物品引出来的射线的几种情况:

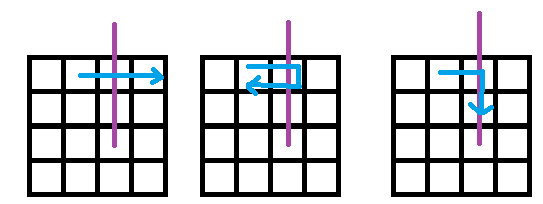
　　然后发现一个格子一个点好像不太好处理，（因为自己智商-inf，所以想不出来不拆点的做法），所以决定把一个格子拆成左右两个点，中间连一条权值为0的双向边，于是对于与路径相交就很好处理了。

　　最后再枚举一下状态，统计答案就行了。

Code

  1 /**
  2  * Codeforces
  3  * Problem#375C
  4  * Accepted
  5  * Time: 31ms
  6  * Memory: 3672k
  7  */
  8 #include <bits/stdc++.h>
  9 using namespace std;
 10 
 11 typedef bool boolean;
 12 typedef pair<int, int> pii;
 13 #define fi first
 14 #define sc second
 15 
 16 const int N = 25, S = 1 << 8;
 17 
 18 typedef class Status {
 19     public:
 20         int x;
 21         int y;
 22         int mark;
 23         
 24         Status (int x = 0, int y = 0, int mark = 0):x(x), y(y), mark(mark) {        }
 25 }Status;
 26 
 27 int n, m;
 28 int co, ct = 0, cb = 0;
 29 pii s;
 30 int val[8];
 31 pii pos[8];
 32 int f[N][N << 1][S];
 33 boolean vis[N][N << 1][S];
 34 boolean exist[N][N << 1];
 35 char str[N];
 36 
 37 inline void init() {
 38     scanf("%d%d", &n, &m);
 39     memset(exist, true, sizeof(exist));
 40     for (int i = 0; i < n; i++) {
 41         scanf("%s", str);
 42         for (int j = 0; j < m; j++) {
 43             if (str[j] == '.')    continue;
 44             exist[i][j << 1] = exist[i][(j << 1) | 1] = (str[j] == 'S');
 45             if (str[j] == 'S')
 46                 s = pii(i, j << 1);
 47             else if (str[j] == 'B')
 48                 pos[8 - (++cb)] = pii(i, j);
 49             else if (str[j] != '#')
 50                 pos[str[j] - '0' - 1] = pii(i, j), ct = max(ct, str[j] - '0');
 51         }
 52     }
 53     memcpy (pos + ct, pos + (8 - cb), sizeof(pii) * cb);
 54     for (int i = 0; i < ct; i++)
 55         scanf("%d", val + i);
 56     co = cb + ct;
 57 }
 58 
 59 const int mov[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
 60 
 61 boolean sameGrid(int x1, int y1, int x2, int y2) {
 62     return (x1 == x2 && (y1 >> 1) == (y2 >> 1));
 63 }
 64 
 65 queue<Status> que;
 66 inline void spfa() {
 67     m = m << 1;
 68     que.push(Status(s.fi, s.sc, 0));
 69     memset(f, 0x3f, sizeof(f));
 70     f[s.fi][s.sc][0] = 0;
 71     while (!que.empty()) {
 72         Status e = que.front();
 73         que.pop();
 74         vis[e.x][e.y][e.mark] = false;
 75         for (int d = 0, x, y, c; d < 4; d++) {
 76             Status eu (e.x + mov[d][0], e.y + mov[d][1], e.mark);
 77             if (eu.x < 0 || eu.x >= n || eu.y < 0 || eu.y >= m)    continue;
 78             if (!exist[eu.x][eu.y])    continue;
 79             c = sameGrid(e.x, e.y, eu.x, eu.y) ? (0) : (1); 
 80             if(!c) {
 81                 x = eu.x, y = eu.y >> 1;
 82                 for (int i = 0; i < co; i++) {
 83                     if (pos[i].sc == y && pos[i].fi > x)
 84                         eu.mark ^= (1 << i);
 85                 }
 86             }
 87             if (f[e.x][e.y][e.mark] + c < f[eu.x][eu.y][eu.mark]) {
 88                 f[eu.x][eu.y][eu.mark] = f[e.x][e.y][e.mark] + c;
 89                 if (!vis[eu.x][eu.y][eu.mark]) {
 90 //                    cerr << eu.x << " " << eu.y << " " << eu.mark << " " << f[eu.x][eu.y][eu.mark] << endl;
 91                     vis[eu.x][eu.y][eu.mark] = true;
 92                     que.push(eu);
 93                 }
 94             }
 95         }
 96     }
 97 }
 98 
 99 inline void solve() {
100     int res = 0;
101     for (int i = 0, cmp; i < (1 << ct); i++) {
102         cmp = 0;
103         for (int j = 0; j < ct; j++)
104             if (i & (1 << j))
105                 cmp += val[j];
106         cmp -= f[s.fi][s.sc][i];
107         if (cmp > res)
108             res = cmp;
109     }
110     printf("%d\n", res);
111 }
112 
113 int main() {
114     init();
115     spfa();
116     solve();
117     return 0;
118 }
posted @ 2018-02-06 14:10  阿波罗2003  阅读(348)  评论(0)  编辑  收藏  举报