退役前8天：数论分块

引例:区间极大值 NKOJ2743

1.怎么分块 ?

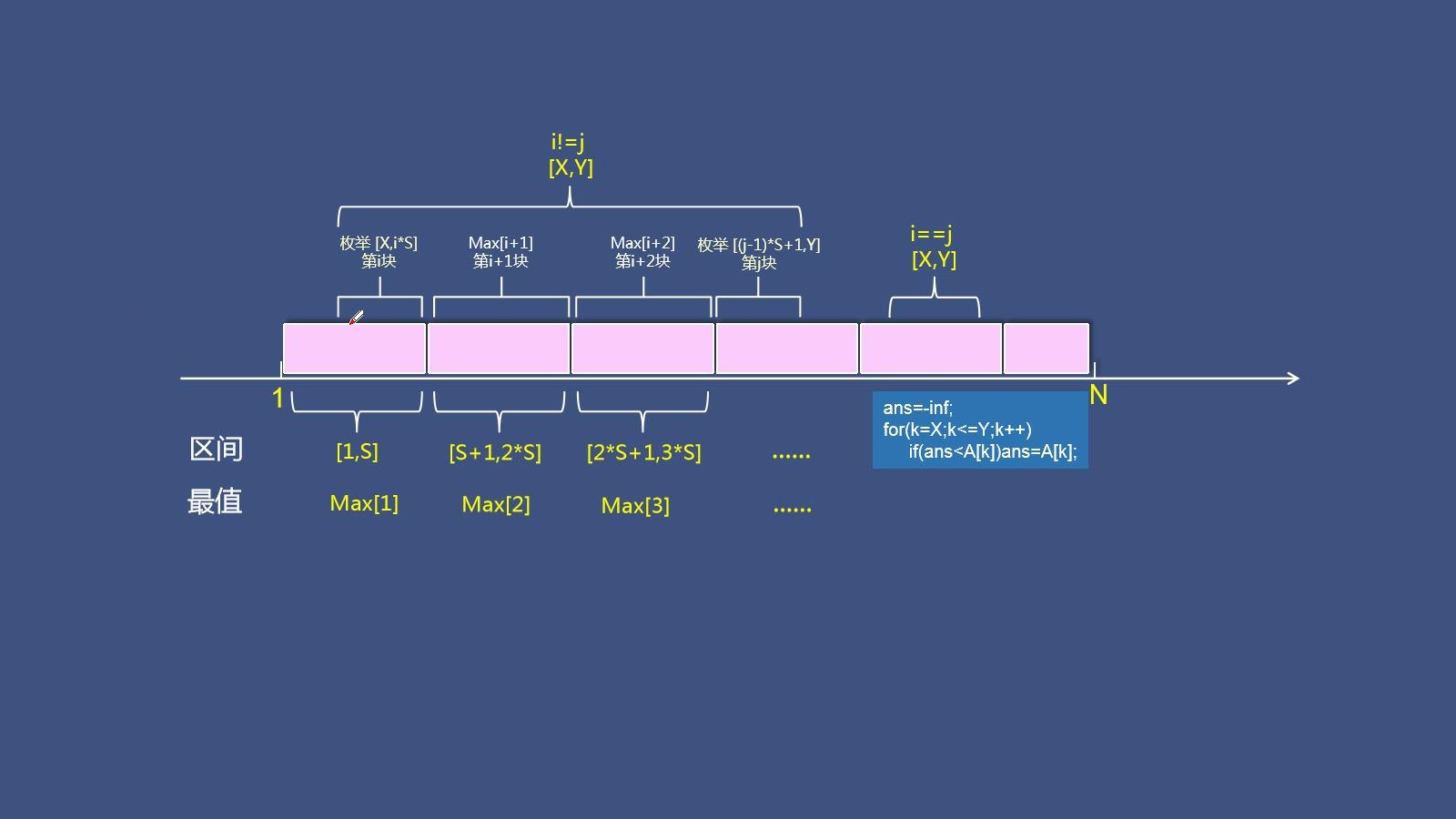
1.把长度为 N 的区间分成若干块，每块长度为 S，共 N / S 块（除最后一块外）；
2.其中第i块表示的区间范围是[(i - 1) * S + 1,i * S];
3.将每一块表示的数字记录下来，其中第i块记录在Max[i]中;

---

2.怎么操作 ?

一.将第X个数A[x]改为A[x] + Y:
1).A[x] = A[x] + Y;
2).找出X所在的块号i = (X - 1) / S + 1,暴力枚举块i中的每个数k，若a[k] > Max[i]则更新Max[i];

二.询问区间[X,Y]中的最大值：
1).计算X所在块号i = (X - 1) / S + 1,Y所在块号j = (Y - 1) / S + 1;
2).若i == j，说明区间[X,Y]在同一块中，直接暴力查询最大值;
3).若i != j，区间[X,Y]的左右两端可能覆盖了某块的一部分，两端直接暴力枚举，中间覆盖的若干整块直接讨论Max[]值.

以下就是代码：

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

const int inf = -1e9;

const int maxn = 1e5 + 5;

int a[maxn];

int Max[maxn];

int s;

void Modify(int x,int y) { 
	int k = (x - 1) / s + 1;
	int L = (k - 1) * s + 1;
	int R = k * s;
	Max[k] = inf;
	a[x] += y;
	for(int i = L;i <= R;i ++) {
		if(a[i] > Max[k]) {
			Max[k] = a[i];
		}
	} 
}

int Query(int x,int y) {
	int i = (x - 1) / s + 1;
	int j = (y - 1) / s + 1;
	int ans = inf;
	if(i == j) {
		for(int k = x;k <= y;k ++) {
			if(ans < a[k]) {
				ans = a[k];
			}
		}
	}  else {
		for(int k = x;k <= i * s;k ++) {
			if(ans < a[k]) {
				ans = a[k];
			}
		}
		for(int k = (j - 1) * s + 1;k <= y;k ++) {
			if(ans < a[k]) {
				ans = a[k];
			} 
		}
		for(int k = i + 1;k < j;k ++) {
			if(ans < Max[k]) {
				ans = Max[k];
			}
		}
	}
	return ans;
}

int main() {
	int n,m;
	cin >> n >> m;
	s = int(sqrt(n));
	int k;
	for(int i = 1;i <= s + 1;i ++) {
		Max[i] = inf;
	}
	for(int i = 1;i <= n;i ++) {
		cin >> a[i];
		k = (i - 1) / s + 1;
		if(a[i] > Max[k]) {
			Max[k] = a[i];
		}
	}
	for(int i = 1;i <= m;i ++) {
		int t,x,y;
		cin >> t >> x >> y;
		if(t == 1) {
			Modify(x,y);
		} else {
			cout << Query(x,y) << endl;
		}
	}
	return 0;
}

---

例2：数列求和 NKOJ2297

1.分块：将数列分成\(\sqrt n\)块，每块\(\sqrt n\)个数。每块维护一个总和sum[]数组。其中sum[i]用于记录第i块中数字的总和。

2.修改：将区间[x,y]整体加上z。

对于每个块维护一个加法标记lazy[],lazy[i]标记第i块被整体增加的数值。对于被[x,y]整块覆盖的块直接修改加法标记(lazy[i] += z)。两端剩余的部分暴力更新被覆盖的每个数的值和对应块的总和(sum[])即可。

3.查询：查询区间[x,y]的总和。

对于中间被[x,y]覆盖的整块，直接讨论该块的总和（第i块为sum[i] + 块长 * lazy[i]）。两端都被部分覆盖的块则暴力统计被覆盖处的总和即可，其中第j块第k个数的值为a[k] + lazy[j]。

4.时间：O(n + m\(\sqrt n\))

以下为代码：

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

const int maxn = 1e5 + 5;
const int inf = -1e9;

int a[maxn];
int Max[maxn];
int Lazy[maxn];

int s;

void Modify(int x,int y,int z) {
	int i = (x - 1) / s + 1;
	int j = (y - 1) / s + 1;
	if(i == j) {
		for(int k = x;k <= y;k ++) {
			a[k] += z;
			if(a[k] > Max[i]) {
				Max[i] = a[k];
			}
		}
	} else {
		for(int k = x;k <= i * s;k ++) {
			a[k] += z;
			if(a[k] > Max[i]) {
				Max[i] = a[k];
			}
		}
		for(int k = (j - 1) * s + 1;k <= y;k ++) {
			a[k] += z;
			if(a[k] > Max[j]) {
				Max[j] = a[k];
			}
		}
		for(int k = i + 1;k < j;k ++) {
			Lazy[k] += z;
		}
	}
}

int Query(int x,int y) {
	int i = (x - 1) / s + 1;
	int j = (y - 1) / s + 1;
	int ans = inf;
	if(i == j) {
		for(int k = x;k <= y;k ++) {
			if(a[k] + Lazy[i] > ans) {
				ans = a[k] + Lazy[i];
			}
		}
	} else {
		for(int k = x;k <= i * s;k ++) {
			if(a[k] + Lazy[i] > ans) {
				ans = a[k] + Lazy[i];
			}
		}
		for(int k = (j - 1) * s + 1;k <= y;k ++) {
			if(a[k] + Lazy[j] > ans) {
				ans = a[k] + Lazy[j];
			}
		}
		for(int k = i + 1;k < j;k ++) {
			if(Max[k] + Lazy[k] > ans) {
				ans = Max[k] + Lazy[k];
			}
		}
	}
	return ans;
}

int main() {
	int n,m;
	cin >> n;
	s = int(sqrt(n));
	int k;
	for(int i = 1;i <= s + 1;i ++) {
		Max[i] = inf;
	}
	for(int i = 1;i <= n;i ++) {
		cin >> a[i];
		k = (i - 1) / s + 1;
		if(a[i] > Max[k]) {
			Max[k] = a[i];
		}
	}
	cin >> m;
	for(int i = 1;i <= m;i ++) {
		char opt[4];
		scanf("%s",opt);
		int x,y;
		cin >> x >> y;
		if(opt[0] == 'A' && opt[1] == 'D') {
			int z;
			cin >> z;
			Modify(x,y,z);
		} else {
			cout << Query(x,y) << endl;
		}
	}
	return 0;
}