OO第一单元总结

一、程序结构分析

1.作业1：简单多项式求导

　　第一次作业实现的是对含幂函数与常数的多项式的求导，因此无论是原函数还是求导的结果都可以分解为 a*x^b形式的单项式。因此item可以作为一个基本的类（这里将这个item类作为了多项式polynomial的private类），其核心的功能就是初始化，求导，以及输出。在单项式上层就是多项式polynomial类与主类直接进行操作。在做此次作业时对arraylist,hashmap了解较少,各个item的信息用静态数组储存，此问题在后续作业中已经做了改进。

　　

　　

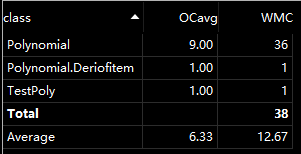
2.作业2：增加连乘与简单三角函数

　　这一次作业增加了两个功能就是连乘与简单三角函数，因为三角函数仅有sin(x)和cos(x)，所以所有单项式都可以化为a*x^b*sin(x)^c*cos(x)^d的标准形式，本质上与第一次标准形式相比多了2个参数，十分相似。因此此次的底层类就是单项式item，在其上的是多项式，又元素为item的链表组成。整体的功能与第一次类似，较大的区别是这一次的求导将返回3个单项式分别加入原式。

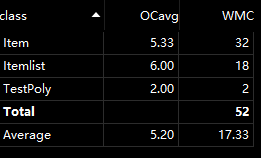
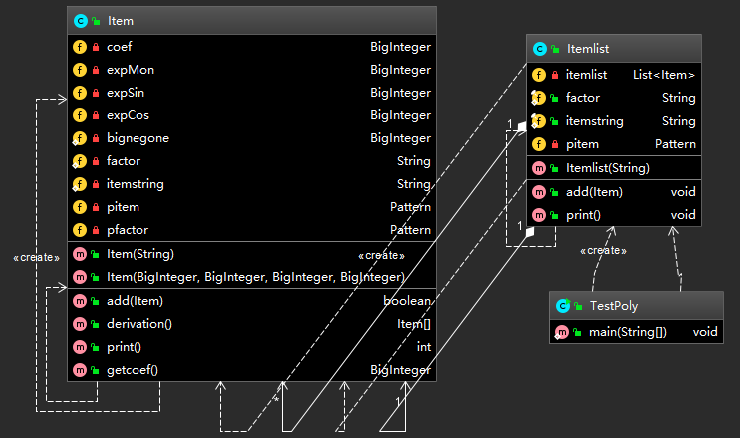
3.增加嵌套与复合函数功能

　　第三次作业与前面有了本质的区别和质的难度提升，无论是简单的合法判断还是求导过程将更为复杂。因为存在嵌套与复合函数，因此前两次的顺序求导将无法完成，这一次求导的过程将依赖于递归。合法判断我使用状态机和正则表达式结合单独进行，判断合法后进行求导操作。在求导操作中存在几个类，多项式，单项式，与因子。多项式求导即为各单项式求导结果之和，单项式则使用函数乘法导数递归求导，因子求导是最底层的对各种不同情况分别求导。因为有嵌套，因此遇到左括号将重新调用多项式求导（不包括三角函数最外层左括号）。

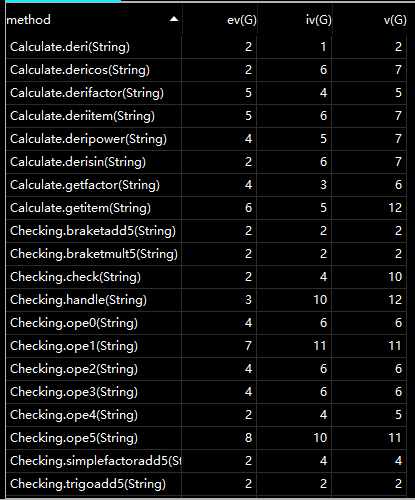
二、程序bug分析

1.第一次作业

　　三次作业因为首项可以选择增加一个运算符，因此我在操作前将首项标准化，即统一为加运算符。在使用String.substring()方法时敲错了第二个参数导致首项增加'+'时会覆盖掉第一项前的第一个字符，这样会忽略少数非法情况如*x。修改参数后解决。

2.第二次作业

　　暂未发现

3.第三次作业

　　暂未发现

三、互测策略分析

　　对于前两次的作业，可以结合代码设计针对性数据（但很耗时）。第三次的代码量基本让针对代码测试变得不可能，因此要从普遍的测试数据入手。测试数据重要的一点是边界性，可以得到很多极端情况。另一个重要的就是脚本，可以快捷的测试多个代码。自动生成此时数据的程序将有很大的帮助，可以减小人的工作量。但是互测阶段一个重要的作用是了解别人的代码的实现思路，并不仅仅是当作一个练习使用脚本的机会。

 

　　

四、Applying Creational Pattern

　　这三次作业中我的分类较为少，很多都归结于同一类下的方法，比如第三次的因子我使用了一个类，用3个private方法对三种不同因子的求导。这样导致代码可移植性与可扩展性较差，可以将类别分的更加细化。