机器学习——逻辑回归 - 指南

机器学习——逻辑回归的实现

1.线性回归

1.线性回归定义
线性回归是一种统计方法，用于模拟因变量（也称为响应变量或结果变量）和一个或多个自变量（也称为解释变量或预测变量）之间的关系。通过拟合数据，线性回归可以用来预测因变量的值，或分析因变量与自变量之间的关系强度和方向。它是回归分析中最基础、应用最广泛的方法之一，具有以下特点：
1.1简单线性回归：只有一个自变量和一个因变量，回归方程的形式为 y = β0 + β1x + ε，其中 y 是因变量，x 是自变量，β0 是截距，β1 是斜率，ε 是误差项。
1.2多元线性回归：涉及多个自变量和一个因变量，回归方程的形式为 y = β0 + β1x1 + β2x2 + … + βnxn + ε，其中 n 是自变量的数量。
2.线性回归原理
线性回归的核心目标是找到一条“最佳拟合线”，使得这条线与所有数据点的距离之和尽可能小。通常使用最小二乘法（Ordinary Least Squares, OLS）来确定这条线。最小二乘法通过最小化观测值与预测值之间的垂直距离的平方和来找到最佳拟合线。对于简单线性回归，其公式如下：
斜率 β1 的计算公式为：

$\beta_1 = \frac{n \sum xy - \sum x \sum y}{n \sum x^2 - (\sum x)^2}$
截距 β0 的计算公式为：

$\beta_0 = \frac{\sum y - \beta_1 \sum x}{n}$
其中，n 是数据点的数量。
例子如图：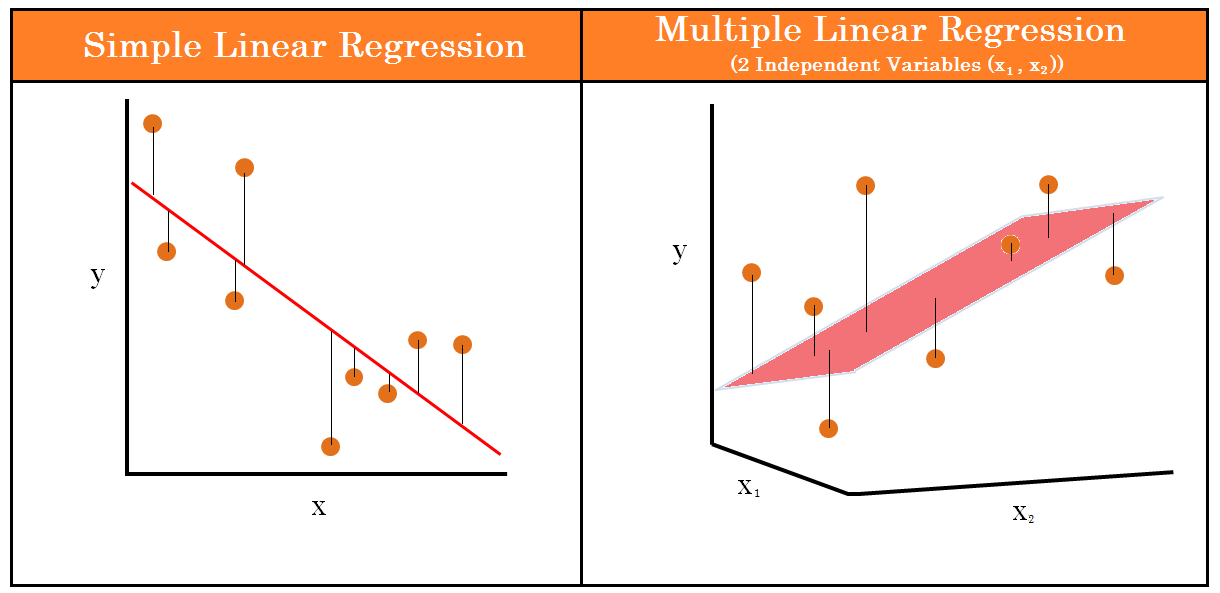
左边是单变量情况，右边是多变量情况
3.线性回归的优化
线性回归的优化是指通过改进模型的训练算法或调整模型的参数，使得模型能够更好地拟合数据，提高预测的准确性。以下是一些常见的优化方法：

梯度下降法
梯度下降法是一种常用的优化算法，通过迭代更新模型参数来最小化损失函数。在每次迭代中，计算损失函数对每个参数的梯度，并沿着梯度的反方向更新参数值。该过程持续进行，直到达到指定的迭代次数或损失函数值在一定范围内变化甚微。
损失函数对参数的偏导数即梯度，用于确定每次更新的方向。学习率是一个超参数，控制参数更新的幅度。学习率过大可能导致模型不收敛，过小则会增加训练时间。此外，梯度下降法有多种变种，包括批量梯度下降、随机梯度下降和小批量梯度下降，它们在计算梯度时使用的数据样本数量不同，各有优缺点。
公式：
损失函数（均方误差）：
$J(\beta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\beta(x^{(i)}) - y^{(i)})^2$
其中， $hβ(x)h_\beta(x)$ 是假设函数， $β\beta$ 是模型参数， $m$ 是训练样本的数量。
梯度更新规则：
$\beta_j := \beta_j - \alpha \frac{\partial J(\beta)}{\partial \beta_j}$
其中， $α\alpha$ 是学习率。

损失函数的优化
损失函数如下图所示，是一个凸函数，我们的目的是达到最低点，也就是损失函数最小。
在这里插入图片描述
多元情况下容易出现局部极值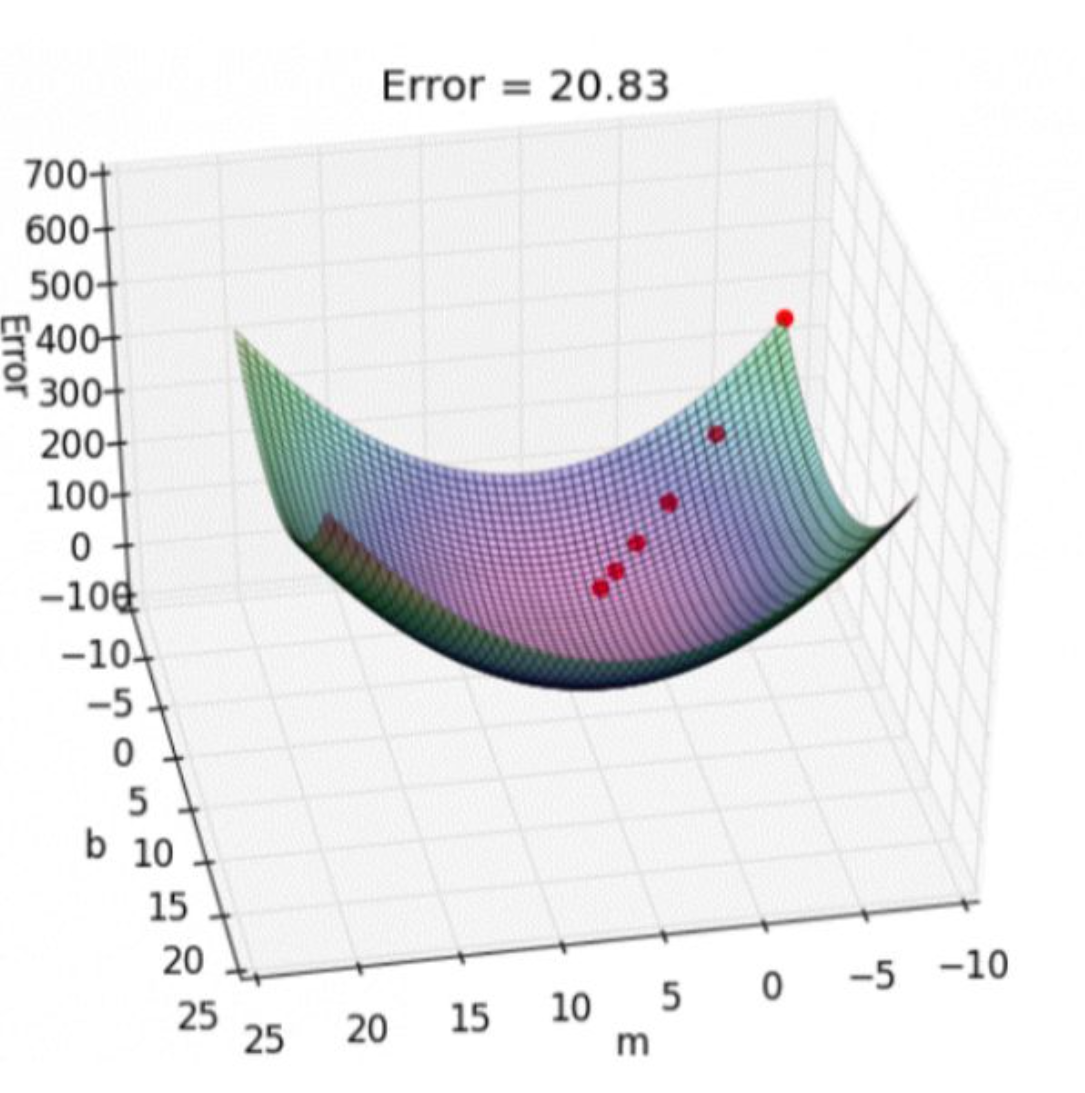

4.线性回归的优缺点
优点：
简单易懂：线性回归模型结构简单，易于解释和理解，可清晰展示自变量与因变量之间的关系。
计算高效：算法成熟，计算复杂度低，能快速处理大规模数据。
应用广泛：在多领域有广泛应用，可处理多种问题。
缺点：
假设限制：基于线性关系、独立性、同方差性和正态性等假设，实际数据可能不完全满足，可能影响模型预测精度和可靠性。
过拟合风险：当自变量过多或数据噪声较大时，容易过拟合，降低模型的泛化能力。
无法处理非线性关系：对于非线性关系，线性回归模型无法有效拟合，需要进行变量变换或采用非线性回归模型。

2.从线性回归到逻辑回归

1.线性回归的局限性
我们先来看线性回归的一个例子，假设我们有一组数据，包含学生的考试成绩和他们是否通过考试（0 表示未通过，1 表示通过）。我们想根据考试成绩来预测学生是否能通过考试。如果使用线性回归模型，其预测结果可能会超出 [0, 1] 的范围，这显然不符合实际意义，因为通过考试的概率应该在 0 到 1 之间。
2.引入逻辑回归
为了解决线性回归在分类问题上的局限性，我们可以对线性回归的输出进行变换，使其结果限制在 [0, 1] 的区间内。逻辑回归通过逻辑函数（logistic function），也称为 Sigmoid 函数，来实现这一点。
3.总结
从线性回归到逻辑回归的引入，主要是为了解决分类问题。线性回归在处理分类问题时存在局限性，因为它的预测结果可能超出合理的范围。逻辑回归通过引入 Sigmoid 函数，将线性回归的输出映射到概率空间，从而使得模型的预测结果符合分类问题的要求。逻辑回归不仅能够给出分类结果，还能提供事件发生的概率，这在许多实际应用场景中是非常有价值的。

3.逻辑回归

1.逻辑回归的定义
逻辑回归模型假设因变量（目标变量）是二元分类变量（如0或1），表示某个事件发生的概率。模型通过逻辑函数（也称为Sigmoid函数）将线性组合的输出转换为概率值。逻辑回归的模型形式如下：
$\ln\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_nx_n$

其中：

( p ) 是因变量为1的概率。
( \beta_0, \beta_1, \ldots, \beta_n ) 是模型参数。
( x_1, x_2, \ldots, x_n ) 是自变量（特征变量）。
通过变形，可以得到 ( p ) 的表达式：
$\frac{1}{1 + e^{-(\beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_nx_n)}}$
2.逻辑回归的原理
逻辑回归 = 线性回归 + sigmoid函数
其核心在于逻辑函数（Sigmoid函数），该函数将任何实数值映射到(0, 1)区间，表示概率值。逻辑函数的公式如下：
$\sigma(z) = \frac{1}{1 + e^{-z}}$

其中，z=β 0+β 1x 1 +β 2x 2+…+β nx n，是自变量的线性组合。

逻辑回归通过最大似然估计（Maximum Likelihood Estimation, MLE）来估计模型参数，使得模型在训练数据上的预测概率与实际结果尽可能接近。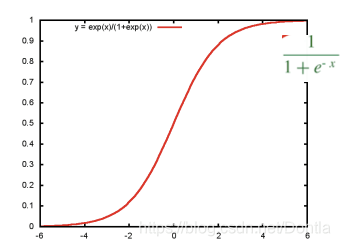
在这里插入图片描述
3.sigmoid函数的作用
逻辑函数（Sigmoid 函数）可以将结果从 $(−∞,+∞)(-\infty, +\infty)$ 映射到 $(0, 1)$ 之间，作为概率。

当 $\rightarrow -\infty$ , $hθ(x)→0h_{\theta}(x) \rightarrow 0$ ；
当 $\rightarrow +\infty$ , $hθ(x)→1h_{\theta}(x) \rightarrow 1$ ；

容易得到决策边界（可以将0.5作为决策边界）：

当 $x < 0$ 时，Sigmoid(x) < 0.5；
当 $x > 0$ 时，Sigmoid(x) > 0.5；

数学特性好，求导容易：
$\cdot (1 - g(z))$
在这里插入图片描述
4.逻辑回归的损失与优化
逻辑回归的损失函数
$\text{cost}(h_\theta(x), y) = - \frac{1}{m} \sum_{i=1}^{m} \left[ y_i \log(h_\theta(x)) + (1 - y_i) \log(1 - h_\theta(x)) \right]$

其中， $hθ(x)h_\theta(x)$ 是样本 $x$ 属于正类的概率。优化的目标就是找到参数 $θ\theta$ 使得损失函数最小。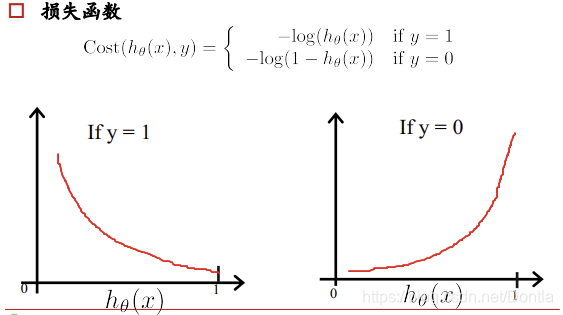
在这里插入图片描述
其中， $y$ 为真实值， $hθ(x)h_\theta(x)$ 为预测值，损失函数值越小越好。

对于损失函数，是损失函数值越小效果就越好
当y=1时，如果预测结果hθ（x）越接近真实结果1，惩罚越小，反之越接近错误结果0，惩罚越大。
当y=0时，如果预测结果hθ（x）越接近真实结果0，惩罚越小，反之越接近错误结果1，惩罚越大。
优化
同样使⽤梯度下降优化算法（一种经典的数值求解算法），去减少损失函数的值。这样去更新逻辑回归前⾯对应算法的权重参数，提升原本属于 1 类别的概率，降低原本是 0 类别的概率。
使用梯度下降算法或其变种来最小化损失函数，更新模型的参数。
梯度下降法
通过 J(w) 对 w 的一阶导数来找下降方向，并以迭代的方式来更新参数
$w_1 := w_1 - \alpha \frac{\partial \text{cost}}{\partial w_1}$

$w_0 := w_0 - \alpha \frac{\partial \text{cost}}{\partial w_0}$
理解：α为学习速率，需要手动指定，α旁边的整体表示方向

沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新W值

使用：面对训练数据规模十分庞大的任务，能够找到较好的结果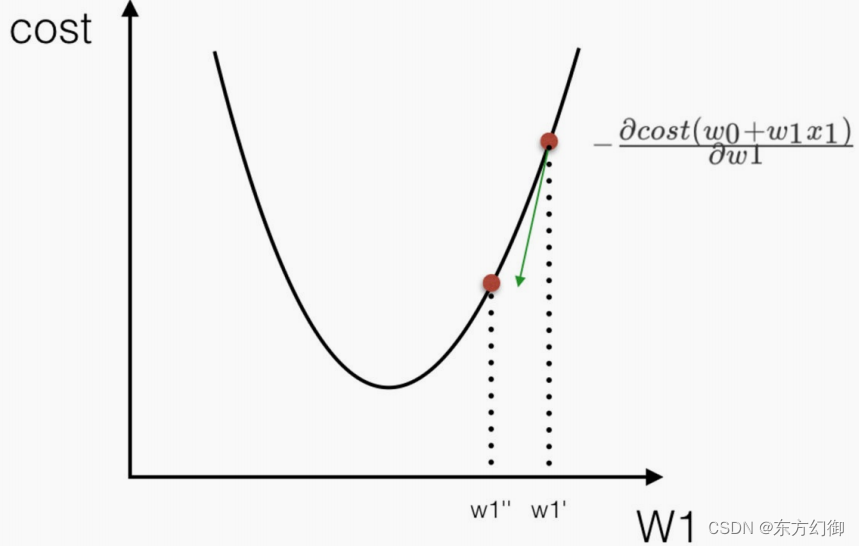
在这里插入图片描述
5.逻辑回归的优缺点
5.1优点：
简单易懂：逻辑回归模型结构简单，易于解释和理解，可清晰展示自变量与因变量之间的关系。
计算高效：算法成熟，计算复杂度低，能快速处理大规模数据。
输出概率：逻辑回归输出的是概率值，可以帮助我们了解模型对每个类别的预测置信度。
应用广泛：在多领域有广泛应用，可处理多种问题。
5.2缺点：
假设限制：逻辑回归假设因变量和自变量之间存在线性关系，如果实际关系是非线性的，模型可能无法准确拟合数据。
过拟合风险：当自变量过多或数据噪声较大时，容易过拟合，降低模型的泛化能力。
无法处理多分类问题：标准逻辑回归模型主要用于二分类问题，对于多分类问题需要扩展为多项逻辑回归（Multinomial Logistic Regression）。
6.Python代码实现逻辑回归
1. 导入所需库

import numpy as np
import matplotlib.pyplot as plt
import os

numpy：用于数值计算，提供数组和矩阵操作功能。
matplotlib.pyplot：用于绘制图形，可视化数据分布和决策边界。
os：用于与操作系统交互，主要用于检查文件是否存在。
2. load_data(file_path) 函数

def load_data(file_path):
    feature_matrix = []
    target_vector = []
    try:
        with open(file_path, 'r') as file_reader:
            for line in file_reader.readlines():
                line_content = line.strip().split()
                feature_matrix.append([1.0, float(line_content[0]), float(line_content[1])])  # 加入偏置项
                target_vector.append(int(line_content[2]))
        return feature_matrix, target_vector
    except FileNotFoundError:
        print(f"文件 {file_path} 不存在，请检查路径和文件名。")
        return None, None

作用：
加载数据集：从指定路径加载数据文件。
处理文件不存在的情况：如果文件不存在，打印错误信息并返回 None。
返回值：返回特征矩阵 feature_matrix 和目标向量 target_vector。
3. sigmoid(input_value) 函数

def sigmoid(input_value):
    return 1.0 / (1 + np.exp(-input_value))

Sigmoid 函数：将输入值映射到 (0, 1) 区间，用于表示概率。
数学公式：公式为 $\sigma(z) = \frac{1}{1 + e^{-z}}$
，其中 z 是输入值。
4. batch_gradient_descent 函数

def batch_gradient_descent(feature_matrix, target_vector, learning_rate=0.001, max_iterations=500):
    feature_array = np.array(feature_matrix)
    target_array = np.array(target_vector).reshape(-1, 1)
    num_samples, num_features = feature_array.shape
    weights = np.ones((num_features, 1))
    for iteration in range(max_iterations):
        hypothesis = sigmoid(np.dot(feature_array, weights))
        error = hypothesis - target_array
        weights = weights - learning_rate * np.dot(feature_array.T, error)
    return weights

使用批量梯度下降法训练逻辑回归模型。
将特征和标签转换为 NumPy 数组，初始化权重 weights 为全 1 的向量。
在每次迭代中，计算当前权重下的假设值（使用 Sigmoid 函数），计算预测值与真实值之间的误差。
根据误差更新权重，更新公式为 weights = weights - learning_rate * np.dot(feature_array.T, error)。
迭代 max_iterations 次后，返回训练后的权重 weights。
5. plot_decision_boundary(model_weights) 函数

def plot_decision_boundary(model_weights):
    feature_matrix, target_vector = load_data(file_path)
    if feature_matrix is None or target_vector is None:
        return
    feature_array = np.array(feature_matrix)
    num_samples = feature_array.shape[0]
    class1_x = []
    class1_y = []
    class0_x = []
    class0_y = []
    for i in range(num_samples):
        if target_vector[i] == 1:
            class1_x.append(feature_array[i, 1])
            class1_y.append(feature_array[i, 2])
        else:
            class0_x.append(feature_array[i, 1])
            class0_y.append(feature_array[i, 2])
    figure = plt.figure()
    axes = figure.add_subplot(111)
    axes.scatter(class1_x, class1_y, s=30, c='green', marker='s', label="Class 1")
    axes.scatter(class0_x, class0_y, s=30, c='blue', marker='o', label="Class 0")
    x_values = np.arange(-3.0, 3.0, 0.1)
    y_values = (-model_weights[0] - model_weights[1] * x_values) / model_weights[2]
    axes.plot(x_values, y_values, label="Decision Boundary")
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.legend()
    plt.show()

绘制数据分布及分类决策边界。
加载数据集，分离出正负样本的特征值。
创建一个新的图形窗口，绘制正样本（Class 1）和负样本（Class 0）的散点图。
绘制决策边界线，线的方程为 (-model_weights[0] - model_weights[1] * x_values) / model_weights[2]。
设置图形的坐标轴标签和图例，并显示图形。
6. 主程序入口

if __name__ == '__main__':
    file_path = r"D:\机器学习\testSet (1).txt"
    if not os.path.exists(file_path):
        print(f"文件 {file_path} 不存在，请检查路径和文件名。")
    else:
        features, labels = load_data(file_path)
        if features is not None and labels is not None:
            print("Sample data points:", features[:3])
            print("Sample labels:", labels[:10])
            trained_weights = batch_gradient_descent(features, labels)
            print("Trained model weights:\n", trained_weights)
            plot_decision_boundary(trained_weights.flatten())

设置文件路径：指定数据文件的路径。
检查文件是否存在：如果文件不存在，打印错误信息。
加载数据：调用 load_data 函数加载数据。
训练模型：调用 batch_gradient_descent 函数训练模型，获取权重参数。
绘制决策边界：调用 plot_decision_boundary 函数绘制数据分布和决策边界。
7.完整代码

import numpy as np
import matplotlib.pyplot as plt
import os
# 1. load_data(file_path) 函数：
# 作用：加载数据集。
# 参数 file_path：指定数据文件的路径。
# 功能：打开文件，逐行读取数据，将特征和标签分别存储在 feature_matrix 和 target_vector 中。
# 返回值：返回特征矩阵 feature_matrix 和标签向量 target_vector。如果文件不存在，则打印错误信息并返回 None。
def load_data(file_path):
    feature_matrix = []
    target_vector = []
    try:
        with open(file_path, 'r') as file_reader:
            for line in file_reader.readlines():
                line_content = line.strip().split()
                feature_matrix.append([1.0, float(line_content[0]), float(line_content[1])])  # 加入偏置项
                target_vector.append(int(line_content[2]))
        return feature_matrix, target_vector
    except FileNotFoundError:
        print(f"文件 {file_path} 不存在，请检查路径和文件名。")
        return None, None
# 2. sigmoid(input_value) 函数：
# 作用：计算输入值的 Sigmoid 函数值。
# 参数 input_value：输入值，通常是一个数值或数组。
# 功能：使用 Sigmoid 函数公式计算输入值的输出值，公式为 1.0 / (1 + np.exp(-input_value))。
# 返回值：返回 Sigmoid 函数的计算结果，范围在 (0, 1) 之间。
def sigmoid(input_value):
    return 1.0 / (1 + np.exp(-input_value))
# 3. batch_gradient_descent 函数：
# 作用：使用批量梯度下降法训练逻辑回归模型。
# 参数：
# feature_matrix：特征矩阵。
# target_vector：目标标签向量。
# learning_rate：学习率，默认为 0.001。
# max_iterations：最大迭代次数，默认为 500。
# 功能：
# 将特征和标签转换为 NumPy 数组。
# 初始化权重 weights 为全 1 的向量。
# 在每次迭代中，计算当前权重下的假设值（使用 Sigmoid 函数）。
# 计算预测值与真实值之间的误差。
# 根据误差更新权重，更新公式为 weights = weights - learning_rate * np.dot(feature_array.T, error)。
# 返回值：返回训练后的权重 weights。
def batch_gradient_descent(feature_matrix, target_vector, learning_rate=0.001, max_iterations=500):
    feature_array = np.array(feature_matrix)
    target_array = np.array(target_vector).reshape(-1, 1)
    num_samples, num_features = feature_array.shape
    weights = np.ones((num_features, 1))
    for iteration in range(max_iterations):
        hypothesis = sigmoid(np.dot(feature_array, weights))
        error = hypothesis - target_array
        weights = weights - learning_rate * np.dot(feature_array.T, error)
    return weights
# 4. plot_decision_boundary(model_weights) 函数：
# 作用：绘制数据分布及分类决策边界。
# 参数 model_weights：训练得到的模型权重。
# 功能：
# 加载数据集，分离出正负样本的特征值。
# 创建一个新的图形窗口。
# 绘制正样本（Class 1）和负样本（Class 0）的散点图，分别使用绿色方块和蓝色圆圈表示。
# 绘制决策边界线。
# 设置图形的坐标轴标签和图例。
# 显示图形。
def plot_decision_boundary(model_weights):
    feature_matrix, target_vector = load_data(file_path)
    if feature_matrix is None or target_vector is None:
        return
    feature_array = np.array(feature_matrix)
    num_samples = feature_array.shape[0]
    class1_x = []
    class1_y = []
    class0_x = []
    class0_y = []
    for i in range(num_samples):
        if target_vector[i] == 1:
            class1_x.append(feature_array[i, 1])
            class1_y.append(feature_array[i, 2])
        else:
            class0_x.append(feature_array[i, 1])
            class0_y.append(feature_array[i, 2])
    figure = plt.figure()
    axes = figure.add_subplot(111)
    axes.scatter(class1_x, class1_y, s=30, c='green', marker='s', label="Class 1")
    axes.scatter(class0_x, class0_y, s=30, c='blue', marker='o', label="Class 0")
    x_values = np.arange(-3.0, 3.0, 0.1)
    y_values = (-model_weights[0] - model_weights[1] * x_values) / model_weights[2]
    axes.plot(x_values, y_values, label="Decision Boundary")
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.legend()
    plt.show()
# 5. if __name__ == '__main__': 主程序入口：
# 作用：程序的主入口，控制程序的流程。
# 设置文件路径：指定数据文件的路径。
# 检查文件是否存在：如果文件不存在，打印错误信息并退出。
# 加载数据：调用 load_data 函数加载数据。
# 打印样本数据和标签：输出前几个样本数据和标签供检查。
# 训练模型：调用 batch_gradient_descent 函数训练模型，得到权重参数。
# 打印权重参数：输出训练得到的权重参数。
# 绘制决策边界：调用 plot_decision_boundary 函数绘制决策边界图。
if __name__ == '__main__':
    file_path = r"D:\机器学习\testSet (1).txt"
    if not os.path.exists(file_path):
        print(f"文件 {file_path} 不存在，请检查路径和文件名。")
    else:
        features, labels = load_data(file_path)
        if features is not None and labels is not None:
            print("Sample data points:", features[:3])
            print("Sample labels:", labels[:10])
            trained_weights = batch_gradient_descent(features, labels)
            print("Trained model weights:\n", trained_weights)
            plot_decision_boundary(trained_weights.flatten())

8.结果图
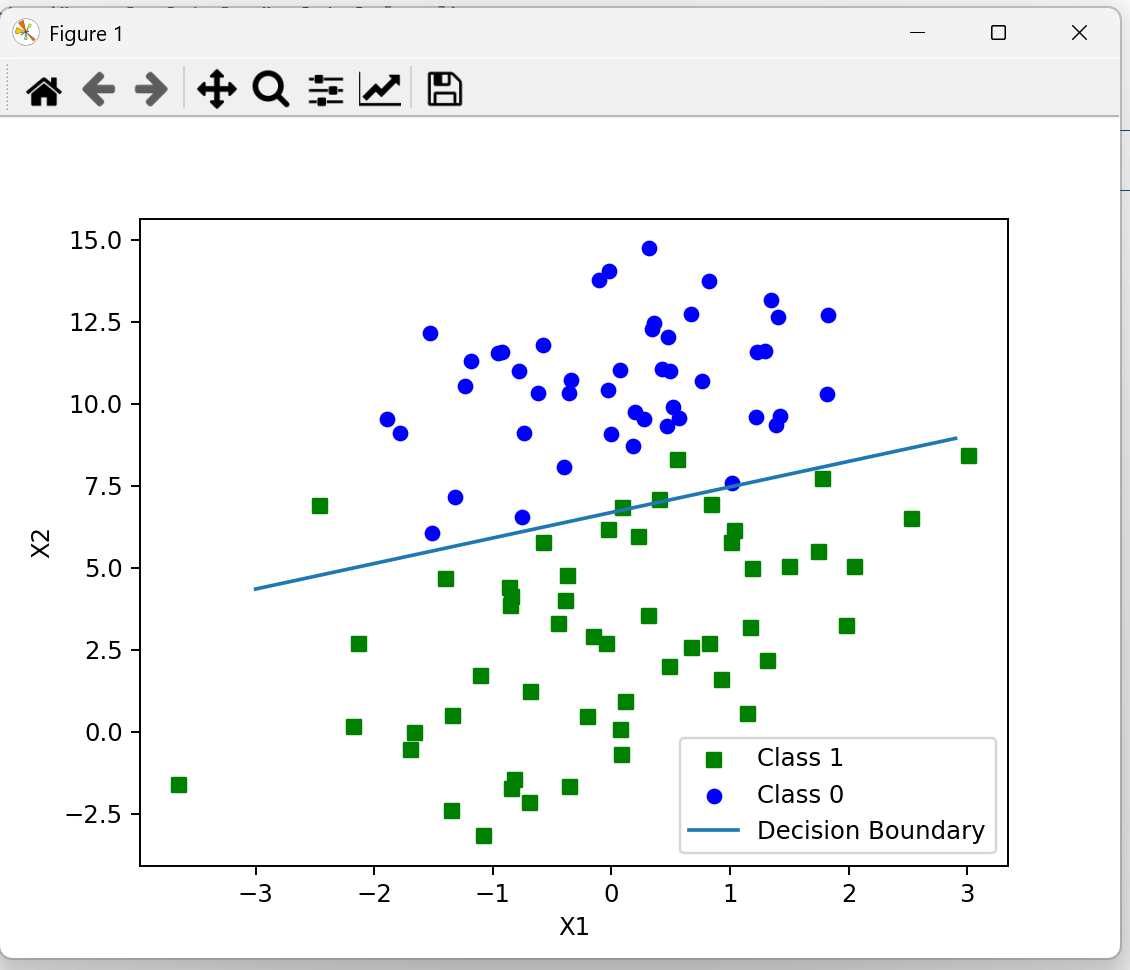
在这里插入图片描述

7.总结

本次实验实现了逻辑回归模型，主要过程如下：
数据准备：加载数据集，分离特征和标签。
模型训练：使用梯度上升算法优化模型参数。其中，批量梯度上升利用所有样本计算梯度，而随机梯度上升每次仅用一个随机样本更新参数。
模型评估：通过可视化决策边界，展示模型的分类效果。
实验结果表明，逻辑回归能够有效处理二分类问题，通过迭代优化找到最优参数，实现对新样本的分类预测。同时，矩阵运算在参数更新过程中发挥了重要作用，体现了其在机器学习算法中的普遍性和高效性。

posted @ 2025-11-06 17:53 yxysuanfa 阅读(6) 评论(0) 收藏举报

刷新页面返回顶部

yxysuanfa