基础网络流
1. 基本概念
1.1 流网络,不考虑反向边
有源点,也有汇点。
可以想象成一条河,每一条边都是一条沟渠,每天边上的权值可以想象成河每秒流过的水量,是一个有限制的值,源点是一个水库,源源不断,汇点可以想象成大海,滚滚长江东逝水...
可以表示为 $G=(V,E)$。
1.2 可行流,不考虑反向边
1.2.1 两个条件:容量限制、流量守恒
容量限制表达式:$0<=f(u,v)<=c(u,v)$,其中 $f(u,v)$ 是值,$c(u,v)$ 是指定好的。
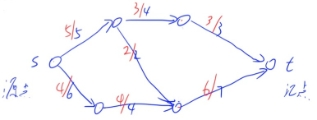
流量守恒:对于任意 $x$ 属于 $V/(S,T)$, $V$ 是点集,如下图所示。

只需满足以上两个条件,就是可行流。
请注意,现在还不需要考虑反向边。
好,现在设可行流为 $f$。
1.2.2 可行流的流量指从源点流出的流量 - 流入源点的流量
$|f|$ 表示每秒从源点流出点的流量,或者是流入汇点的流量。
1.2.3 最大流是指集合中最大可行流。
下图,就是一个合法的图啦。
1.3 残留网络,考虑反向边,残留网络的可行流f' + 原图的可行流f = 原题的另一个可行流
这个东西,是针对流网络的一条可行流的。
可行流不同,残留网络也不同,一般记为 $G_f$。
首先,点集和原图一样。
其次,边集,不仅包含原来的所有边,同时包含 $E$ 的所有反向边。
原来的容量是 $c(u,v)$,现在我们打一个撇。
他取决于你还能增加多少,还有你退回去的情况,如下图。
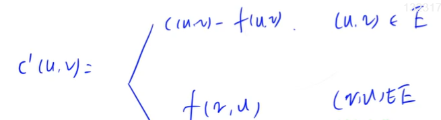
(1) $|f' + f| = |f'| + |f|$
(2)$ |f'| $可能是负数
1.4 增广路径
从源点出发,沿着容量大于 $0$ 的边走,若能走到终点,那么就是一个增广路径。
容易发现一定是可行流。
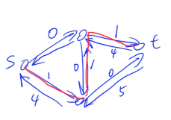
下图的红色边便是合法的增广路径。
1.5 割
1.5.1 割的定义
在流网络 $G=(V,E)$ 把点集 $V$ 分成两个不重不漏的子集,并使得源点和汇点在不同的部分,把划分的结果叫做割。
下图可以形象地展示。

1.5.2 割的容量:$c(S ,T)=\sum_{u \in S} \sum_{v \in T}$
不考虑反向边,“最小割”是指容量最小的割。
1.5.3 割的流量:$f(S, T)=\sum_{u \in S} \sum_{v \in T} f(u, v) . -\sum_{u \in T} \sum_{v \in S} f(u, v) .$
考虑反向边,$f(S, T) <= c(S, T)$,可以自行思考原因。
1.5.4 对于任意可行流f,任意割 $[S, T],|f| = f(S, T)$
1.5.5 对于任意可行流f,任意割 $[S, T],|f| <= c(S, T)$
1.5.6 最大流最小割定理
(1) 可以流 $f$ 是最大流
(2) 可行流f的残留网络中不存在增广路
(3) 存在某个割 $[S, T],|f| = c(S, T)$
结论:三个条件相互等价,证明自己看算导。
1.6. 算法
1.6.1 $EK$ $O(nm^2)$
#include<bits/stdc++.h> using namespace std; int n,m,S,T,head[20005],u,v,w,nxt[200005],ver[200005],tot,d[200005],f[200005],q[200005],pre[200005]; bool st[200005]; void add(int a,int b,int c){ ver[tot]=b; f[tot]=c; nxt[tot]=head[a]; head[a]=tot++; ver[tot]=a; f[tot]=0; nxt[tot]=head[b]; head[b]=tot++; } bool zengguang(){ int hh=0,tt=0; memset(st,0,sizeof(st)); q[0]=S; st[S]=1; d[S]=1e8; while(hh<=tt){ int t=q[hh++]; for(int i=head[t];i!=-1;i=nxt[i]){ int v=ver[i]; if(!st[v]&&f[i]){ st[v]=1; d[v]=min(d[t],f[i]); pre[v]=i; if(v==T){ return 1; } q[++tt]=v; } } } return 0; } int ek(){ int r=0; while(zengguang()){ r+=d[T]; for(int i=T;i!=S;i=ver[pre[i]^1]){ f[pre[i]]-=d[T]; f[pre[i]^1]+=d[T]; } } return r; } int main(){ memset(head,-1,sizeof(head)); scanf("%d%d%d%d",&n,&m,&S,&T); for(int i=1;i<=m;i++){ scanf("%d%d%d",&u,&v,&w); add(u,v,w); } printf("%d",ek()); return 0; }
1.6.2 $Dinic$ $O(n^2m)$
#include<bits/stdc++.h> using namespace std; int n,m,S,T,ver[200005],nxt[200005],val[200005],head[200005],a,b,c,tot,d[200005],cur[200005],q[200005]; void add(int u,int v,int w){ ver[tot]=v; nxt[tot]=head[u]; val[tot]=w; head[u]=tot++; ver[tot]=u; nxt[tot]=head[v]; val[tot]=0; head[v]=tot++; } bool bfs(){ int hh=0,tt=0; memset(d,-1,sizeof(d)); q[0]=S; d[S]=0; cur[S]=head[S]; while(hh<=tt){ int tmp=q[hh++]; for(int i=head[tmp];~i;i=nxt[i]){ int vv=ver[i]; if (d[vv]==-1&&val[i]){ d[vv]=d[tmp]+1; cur[vv]=head[vv]; if(vv==T){ return 1; } q[++tt]=vv; } } } return 0; } int find(int u,int limit){ if(u==T){ return limit; } int flow=0; for(int i=cur[u];~i&&flow<limit;i=nxt[i]){ cur[u]=i; int vv=ver[i]; if(d[vv]==d[u]+1&&val[i]){ int tmp=find(vv,min(val[i],limit-flow)); if(!tmp){ d[vv]=-1; } val[i]-=tmp; val[i^1]+=tmp; flow+=tmp; } } return flow; } int dinic(){ int r=0,flow; while(bfs()){ while(flow=find(S,1e8)){ r+=flow; } } return r; } int main(){ scanf("%d%d%d%d",&n,&m,&S,&T); memset(head,-1,sizeof(head)); while(m--){ scanf("%d%d%d",&a,&b,&c); add(a,b,c); } printf("%d",dinic()); return 0; }
最大流问题一般分析方法:
给我们一个问题 $P$,我们要建立一个流网络 $G$。先看问题的所有可行集合,随后看看可行流集合,证明其中是以一 一对应的。随后即可得出,左边的最值(原问题的最大/最小值)等于右边的最值(最大/小可行流)。
事实上,最小割也是这样考虑的。
1.7 应用
1.7.1 二分图
(1) 二分图匹配
典型例题:A集合 $m$ 个点和 B集合 $n-m$ 个点两两配对,问最大匹配数和匹配方案。
题解: https://www.luogu.com.cn/problem/P2756
根据流网络的定义,先建立源点 $S$ 和汇点 $T$,从源点 $S$向所有A集合中的点建立一条容量为 $1$ 的边,从所有 A集合中的点向其可搭档的 B集合中的点建立一条容量为 $1$ 的边,从所有 B集合汇点T建立一条容量为 $1$ 的边。整个流网络的可行流中的最大流便是最大匹配方案。
AC代码:
#include<bits/stdc++.h> using namespace std; int m,n,ver[200005],nxt[200005],val[200005],head[200005],a,b,c,tot,d[200005],cur[200005],q[200005],S,T,aa,bb; void add(int u,int v,int w){ ver[tot]=v; nxt[tot]=head[u]; val[tot]=w; head[u]=tot++; ver[tot]=u; nxt[tot]=head[v]; val[tot]=0; head[v]=tot++; } bool bfs(){ int hh=0,tt=0; memset(d,-1,sizeof(d)); q[0]=S; d[S]=0; cur[S]=head[S]; while(hh<=tt){ int tmp=q[hh++]; for(int i=head[tmp];~i;i=nxt[i]){ int vv=ver[i]; if (d[vv]==-1&&val[i]){ d[vv]=d[tmp]+1; cur[vv]=head[vv]; if(vv==T){ return 1; } q[++tt]=vv; } } } return 0; } int find(int u,int limit){ if(u==T){ return limit; } int flow=0; for(int i=cur[u];~i&&flow<limit;i=nxt[i]){ cur[u]=i; int vv=ver[i]; if(d[vv]==d[u]+1&&val[i]){ int tmp=find(vv,min(val[i],limit-flow)); if(!tmp){ d[vv]=-1; } val[i]-=tmp; val[i^1]+=tmp; flow+=tmp; } } return flow; } int dinic(){ int r=0,flow; while(bfs()){ while(flow=find(S,1e8)){ r+=flow; } } return r; } int main(){ scanf("%d%d",&m,&n); S=0; T=n+1; memset(head,-1,sizeof(head)); for(int i=1;i<=m;i++){ add(S,i,1); } for(int i=m+1;i<=n;i++){ add(i,T,1); } while(scanf("%d%d",&aa,&bb),aa!=-1){ add(aa,bb,1); } printf("%d\n",dinic()); for(int i=0;i<tot;i+=2){ if(ver[i]>m&&ver[i]<=n&&!val[i]){ printf("%d %d\n",ver[i^1],ver[i]); } } return 0; }
(2) 二分图多重匹配
假设有来自 $m$ 个不同单位的代表参加一次国际会议。
每个单位的代表数分别为 $ r_{i}(i=1,2, \ldots, m) $ 。
会议餐厅共有 $n$ 张餐桌,每张餐桌可容纳 $c_{i}(i=1,2, \ldots, n) $ 个代表就餐。
为了充分交流,希望从同一个单位来的代表不在同一个餐桌就餐。
请给出满足要求的代表就餐方案。
题解:https://www.luogu.com.cn/problem/P3254,直观的建图。
1.7.2 上下界网络流
(1) 无源汇上下界可行流
(2) 有源汇上下界最大流
(3) 有源汇上下界最小流
1.7.3 多源汇最大流



