最长公共子串

最长公共子串

​ 给定两个字符串str1和str2，返回两个字符串的最长公共子串。

此处计算的是两个字符串的最长公共子串，子串不同于子序列，子串要求必须是一串连续的字符。

方法一

​ 使用经典的动态规划方法，首先定义一个动态规划数组dp，dp[i][j]表示的含义是以在str1中第i个字符和str2中第j个字符结尾的最长公共字串的长度。那么状态转移表达式就是：

​ 1、如果str1[i] == str2[j]

dp[i][j] = dp[i-1][j-1] + 1;

​ 2、如果str1[i] ！= str2[j]

dp[i][j] = 0

​ 初始化：

​ 对于dp[i][0]，如果str1[i] == str2[0]，则dp[i][0] = 1;

​ 对于dp[0][j]，如果str1[0] == str2[j]，则dp[0][j] = 1;

public static int longestCommonStr(String text1, String text2){

    int n = text1.length();
    int m = text2.length();

    int[][] dp = new int[n][m];
    int max_length = 0;
    for (int i = 0; i < text1.toCharArray().length; i++) {

        if (text1.charAt(i) == text2.charAt(0)){
            dp[i][0] = 1;
            max_length = 1;
        }
    }
    for (int j = 0;j < text2.toCharArray().length;j++){

        if (text2.charAt(j) == text1.charAt(0)){
            dp[0][j] = 1;
        }
    }
    for (int i = 1; i < n; i++) {

        for (int j = 1; j < m; j++) {

            if (text1.charAt(i) == text2.charAt(j)){
                dp[i][j] = dp[i-1][j-1] + 1;
            }else {
                dp[i][j] = 0;
            }
            max_length = max_length>dp[i][j]?max_length:dp[i][j];
        }

    }
    return max_length;
}

​ 时间复杂度为O(n*m)，空间复杂度为O(n*m)

方法二

​ 优化上面算法的空间复杂度，将其由O(n*m)优化为常量级别的O(1)

​ 在上面，我们定义的状态转移数组，是一个二维矩阵，其中每一个元素代表的含义就是以在str1中第i个字符和str2中第j个字符结尾的最长公共字串的长度，而dp[i][j]的值要么是0，要么就是在状态转移矩阵其位置的左上方的那个值的基础上加1得到。

​ 比如字符串 "abcde" 和 "bebcd"，它的状态转移矩阵是：

	b	e	b	c	d
a	0	0	0	0	0
b	1	0	1	0	0
c	0	0	0	2	0
d	0	0	0	0	3
e	0	1	0	0	0

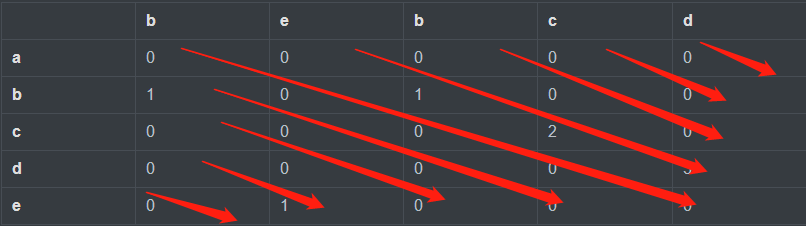
​ 如果按照上图中的斜线来计算的话，那么就无需再使用状态转移数组，而只需变量就可以了。

​ 在按照斜线进行计算之前，先定义一个变量len，它用于记录状态转移矩阵中当前位置的左上方位置的值，初始值为0，计算的过程中首先判断if str1[i] == str2[j]：

​ 如果相等，那么len++；否则len=0

​ 我们从右上方的斜线开始计算，然后依次向左移动，计算左边的斜线；当无法向左移动的时候，再向下移动，当最左下方的斜线计算完毕以后，整个计算就完毕了。

public static int longestCommonStr2(String text1, String text2){

    int m = text1.length();
    int n = text2.length();

    int row = 0;
    int col = n - 1;
    int max_length = 0;

    while (row < m){
        int i = row;
        int j = col;
        int len = 0;
        while (j < n && i < m){

            if (text1.charAt(i) == text2.charAt(j)){
                len++;
            }else {
                len = 0;
            }
            j++;
            i++;
        }
        max_length = max_length > len ? max_length : len;

        if (col > 0){
            col--;
        }else {
            row++;
        }
    }

    return max_length;

}

​ 此算法的空间复杂度为O(1)