FFT什么的
这里只有公式&做法,没有复杂的证明(其实是因为弱鸡yww不会)
参考自国家集训队论文&各个博客
多项式
一个以\(x\)为变量的多项式定义在一个代数域\(F\)上,将函数\(A(x)\)表示为形式和:
我们称\(a_0,a_1,\ldots,a_{n-1}\)为多项式的系数,所有系数都属于数域\(F\),典型的情形是负数集合\(C\)。
如果一个多项式的最高次的非零系数是\(a_k\),则称\(A(x)\)的次数是\(k\)。任何严格大于一个多项式次数的整数都是该多项式的次数界。因此,对于次数界为\(n\)的多项式\(C(x)\),其次数可以是\(0\)~\(n-1\)之间的任何整数,包括\(0\)和\(n-1\)。
我们在多项式上可以定义很多不同的运算。
多项式加法
如果\(A(x)\)和\(B(x)\)是次数界为\(n\)的多项式,那么他们的和也是一个次数界为\(n\)的多项式\(C(x)\)。对于所有属于定义域的\(x\),都有\(C(x)=A(x)+B(x)\)。也就是说,若
则
其中
例如,如果
则
多项式乘法
如果\(A(x)\)是次数界为\(n\)的多项式,\(B(x)\)是次数界为\(m\)的多项式,那么他们的乘积是一个次数界为\(n+m\)的多项式\(C(x)\)。其中
例如,如果
则
多项式的表示
系数表达
对一个次数界为\(n\)的多项式\(A(x)=\sum_{j=0}^{n-1}a_jx^j\)而言,其系数表达式一个由系数组成得到向量\(a=(a_0,a_1,\cdots,a_{n-1})\)
我们可以用秦久韶算法在\(O(n)\)的时间内求出多项式在给定点\(x_0\)的值,即求值运算:
类似的,对于两个分别用系数向量\(a=(a_0,a_1,\cdots,a_{n-1}),b=(b_0,b_1,\cdots,b_{n-1})\)表示的多项式进行相加时,所需的时间是\(O(n)\)。我们只用输出系数向量\(c=(c_0,c_1,\cdots,c_{n-1})\),其中\(c_i=a_i+b_i\)。
现在来考虑两个用系数形式表达的次数界为\(n\)的多项式\(A(x),B(x)\)的乘法运算,所需要的时间是\(O(n^2)\)。系数向量\(c\)也称为输入向量\(a,b\)的卷积。\(c=a\otimes b\)。
点值表达
一个次数界为\(n\)的多项式的点值表达就是一个有\(n\)个点值对所组成的集合。
使得对\(k=0,1,\cdots,n-1\),所有\(x_k\)各不相同且\(y_k=A(x_k)\)。
一个多项式可以有很多不同的点值表达,因为可以采用\(n\)个不同的点构成的集合作为这种表示方法的基。
朴素的求值是\(O(n^2)\)的。
求值的逆称为插值。当插值多项式的次数界等于已知的点值对的数目时,插值才是明确的。
我们可以在用高斯消元在\(O(n^3)\)内插值,也可以用拉格朗日插值在\(O(n^2)\)内插值。
以上求值和插值可以将多项式的系数表达和点值表达进行相互转化,上面给出的算法的时间复杂度是\(O(n^2)\),但我们可以巧妙地选取\(x_k\)来加速这一过程,使其运行时间变为\(O(nlogn)\)。
对于许多多项式相关的操作,点值表达式很便利的。
对于加法,如果\(C(x)=A(x)+B(x)\)。给定\(A\)的点值表达
和\(B\)的点值表达
(注意,\(A\)和\(B\)在相同的\(n\)个位置求值),则\(C\)的点值表达是
因此,对两个点值形式表示的次数界为\(n\)的多项式相加,时间复杂度是\(O(n)\)。
类似的,如果\(C(x)=A(x)B(x)\),我们需要\(2n\)个点值对才能插出\(C\)。给定\(A\)的点值表达
和\(B\)的点值表达
(注意,\(A\)和\(B\)在相同的\(2n\)个位置求值),则\(C\)的点值表达是
因此,对两个点值形式表示的次数界为\(n\)的多项式相乘,时间复杂度是\(O(n)\)。
最后,我们考虑一个采用点值表达的多项式,如何求其在某个新点上的值。最简单的方法是把该多项式转成系数形式表达,然后在新点处求值。
系数形式表示的多项式的快速乘法
如果我们选\(n\)次单位复数根作为求值点,我们可以在\(O(nlogn)\)内求值和插值。我们先在对这两个多项式\(A,B\)求值之前添加\(n\)个\(0\),使其次数界加倍为\(2n\)。现在我们采用“\(2n\)次单位复数根”作为求值点。
DFT&FFT&IDFT
单位复数根
\(n\)次单位复数根是满足\(w^n=1\)的复数\(w\)。\(n\)次单位复数根恰好有\(n\)个,对于\(k=0,1,\cdots,n-1\),这些根是\(e^{\frac{2\pi ik}{n}}\)。\(w_n=e^\frac{2\pi i}{n}\)称为主\(n\)次单位根,所有其他\(n\)次单位复数根都是\(w_n\)的幂次。这\(n\)个\(n\)次单位复数根在乘法意义下形成了一个群,即\(w_n^jw_n^k=w_n^{(j+k)mod~n}\),而且这\(n\)个\(n\)次单位复数根均匀分布在以复平面的原点为圆心的单位半径的圆周上。(图片from zjt)
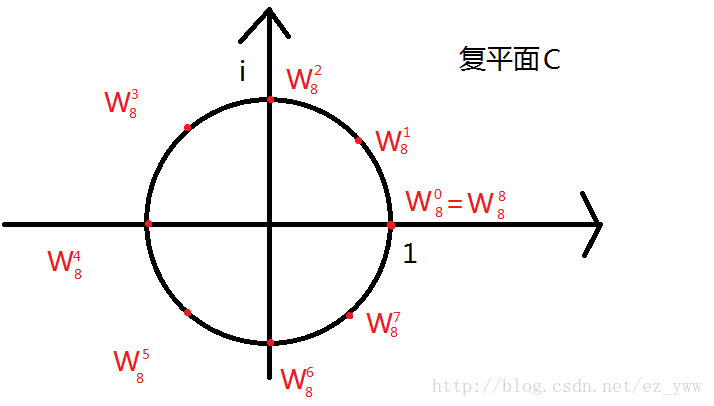
消去引理:对任何整数\(n\geq 0,k\geq 0,d>0\),
DFT
回顾一下,我们希望计算次数界为\(n\)的多项式\(A(x)\)在\(w_n^0,w_n^1,\cdots,w_n^{n-1}\)处的值(即在\(n\)个\(n\)次单位复数根处)。对于\(k=0,1,\cdots,n-1\),定义结果\(y_k\):
向量\(y=(y_0,y_1,\cdots,y_{n-1})\)就是系数向量\(a\)的离散傅里叶变换(DFT),我们也记为\(y=DFT_n(a)\)。
FFT
利用单位复数根的特殊性质,我们可以在\(O(nlogn)\)内计算出\(DFT_n(a)\)。这里假设\(n\)是\(2\)的幂。
FFT利用了分治策略。
我们令\(a=(a_0,a_1,\cdots,a_{n-1}),a_1=(a_0,a_2,\cdots,a_{n-2}),a_2=(a_1,a_3,\cdots,a_{n-1})\)
对于\(k<\frac n2\)有:
对于\(k\geq \frac n2\)有:
这样我们把\(y_1,y_2\)合并为\(y\)的时间复杂度是\(O(n)\)。所以总的时间复杂度是
IDFT
通过推导公式,我们得到:
所以我们可以用类似FFT的方法在\(O(n\log n)\)内求出\(IDFT_n(y)\)
多项式乘法
我们可以在\(O(n)\)内补\(0\),\(O(n\log n)\)内求值,\(O(n)\)内点值乘法,\(O(n\log n)\)内插值。所以我们可以在\(O(n\log n)\)内求出\(a\otimes b\)。
蝶形运算
我们把由\({y_1}_k,{y_2}_k,w_n^k\)得到\(y_k,y_{k+\frac n2}\)的过程称为蝴蝶操作。
我们发现,递归时\(a\)是长这样的:
总的蝶形运算是长这样的:
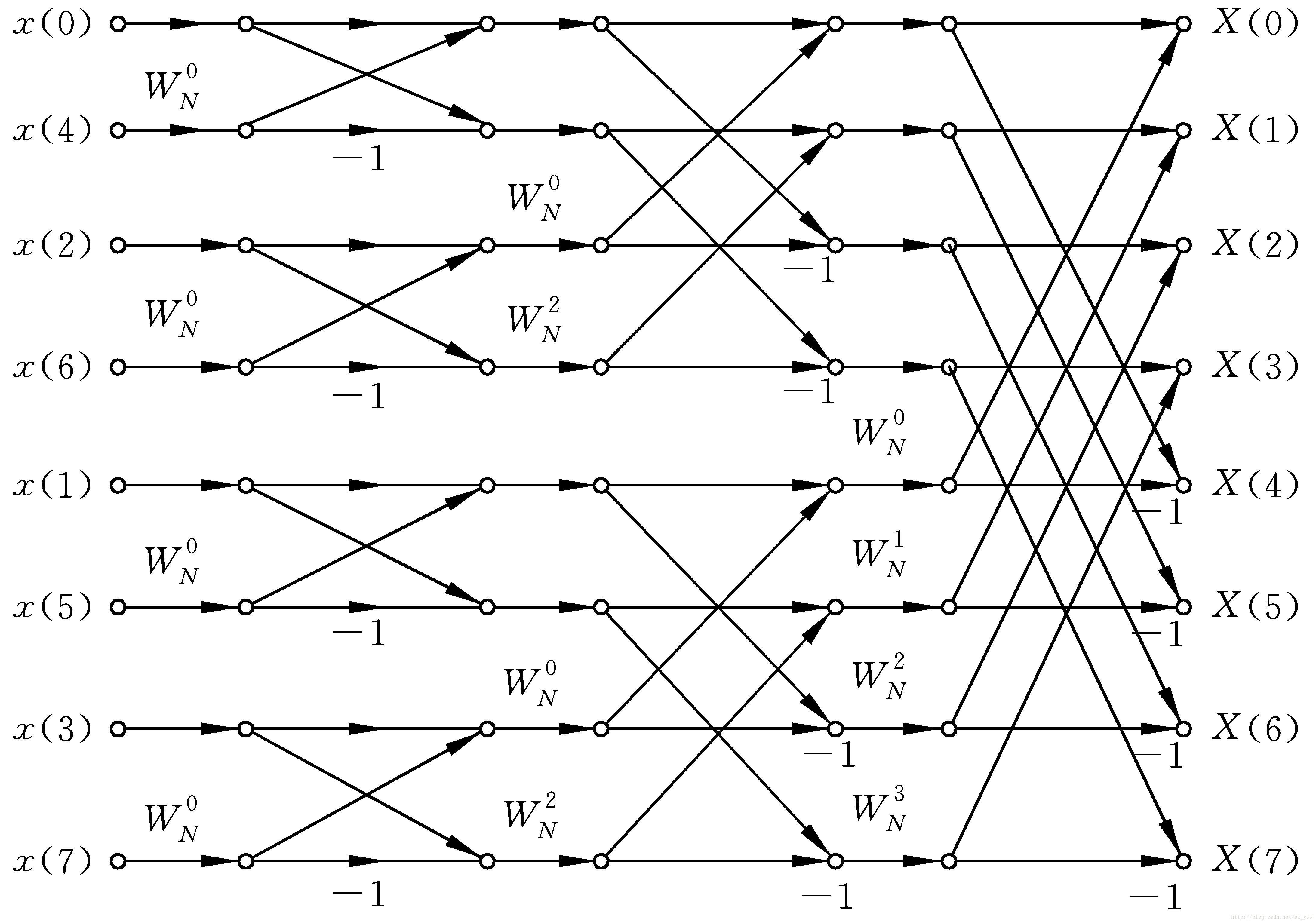
可以发现,最后\(a_i\)是原来的\(a_{rev(i)}\)。所以我们可以交换\(a_i,a_{rev(i)}\),然后一层层来做。这样可以减小常数。
NTT
在某些时候,我们需要求模\(p\)意义下的卷积。
先求出\(p\)的原根\(g\),可以发现,\(g^{\frac{p-1}{n}}\)与\(w_n\)的性质类似。所以我们可以用\(g^{\frac{p-1}{n}}\)来代替\(w_n\)。
时间上的优化
当我们要算两个多项式 \(A(x), B(x)\) 的乘积的时候,普通的做法是先把 \(a,b\) 两个序列 DFT,再点乘,再 IDFT 回去。
但是我们还有一种方法:
令\(t_j=(a_j+b_j)+(a_j-b_j)i,S=T\times T\)
\(s_j\)的实部为
这样我们就可以求出\(S=T\times T\),然后把\(s_j\)除以\(4\)。
这个方法可以把\(3\)次DFT改成\(2\)次DFT。
多项式求导
给定\(A(x)=\sum_{i\geq 0}a_ix^i\),定义\(A(x)\)的形式导数为
多项式积分
给定\(A(x)=\sum_{i\geq 0}a_ix^i\),则
多项式求逆
多项式\(A(x)\)存在乘法逆元的充要条件是\(A(x)\)的常数项存在乘法逆元。
下面介绍一个\(O(n~log~n)\)计算乘法逆元的算法,它的本质是牛顿迭代法
首先求出\(A(x)\)常数项的逆元\(b\),令\(B(x)\)的初始值为\(b\)。
假设已求出满足
的\(B(x)\),则
我们可以用\(O(n~log~n)\)的时间计算出\(2B(x)-B(x)^2A(x)\),并将它赋值给\(B(x)\)进行下一次迭代。每迭代一次,\(B(x)\)的有效项数\(n\)都会增加一倍。于是该算法的时间复杂度为
多项式开根
已知\(A(x)\),求\(B(x)\)使得
先求出\(A(x)\)常数项的平方根\(b\)(可以用二次剩余的东西来算,但我只会暴力算),令\(B(x)\)的初始值为\(b\)。
假设已求出满足
的\(B(x)\),则
我们可以在\(O(n\log n)\)内算出\(\frac{B(x)^2+A(x)}{2B(x)}=\frac{B(x)}{2}+\frac{A(x)}{2B(x)}\),并把它赋值给\(B(x)\)。
时间复杂度:\(O(n\log n)\)
多项式ln
给定形式幂级数\(A(x)=\sum_{i\geq 1}a_ix^i\),定义
给定多项式\(A(x)=1+\sum_{i\geq 1}a_ix^i\),令
则
只需要求出\(A(x)\)的乘法逆元,就可以求出\(\ln(A(x))\)
多项式exp
给定形式幂级数\(A(x)=\sum_{i\geq 1}a_ix^i\),定义
令\(f(x)=e^{A(x)}\),可得到一个关于\(f(x)\)的方程
考虑用牛顿迭代解这一方程。首先\(f(x)\)的常数项是容易确定的(就是\(1\))。
设以求得\(f(x)\)的前\(n\)项\(f_0(x)\),即
作泰勒展开得
即
把上面那个式子带入得
时间复杂度:\(O(n\log n)\)
多项式求幂
给你\(A(x),k\),求\(A^k(x)\)。
设\(A(x)\)中最低次数项是\(cx^d\),那么先把整个多项式除以\(cx^d\),再求\(\ln\),把整个多项式乘以\(k\),再求\(\exp\),再乘上\(c^kx^{kd}\)。
时间复杂度:\(O(n\log n)\)
多项式除法
给你\(A(x),B(x)\),求两个多项式\(D(x),R(x)\)满足
若\(A(x)\)是一个\(n\)阶多项式,则
举个例子:比如说
相当于把\(A(x)\)的系数反转。
我们设\(A(x)\)是\(n\)阶多项式,\(B(x)\)是\(m\)阶多项式,\(D(x)\)是\(n-m\)阶多项式,\(R(x)\)是\(m-1\)阶多项式。我们把上个式子的\(x\)成\(\frac1x\),然后全部乘上\(x^n\)
然后我们把这个式子放在模\(x^{n-m+1}\)意义下,得到
因为\(D(x)\)的次数是\(n-m\),所以不会受模意义的影响。
然后把\(D(x)\)带入到原来的式子中,就可以算出\(R(x)\)了。
时间复杂度:\(O(n\log n)\)
多点求值
给你一个多项式\(A(x)\)和\(n\)个点\(x_0,x_1,\cdots,x_{n-1}\),求这个多项式在这\(n\)个点处的值,即求\(A(x_0),A(x_1),\cdots,A(x_{n-1})\)。
考虑一个简单的做法:构造\(B_i(x)=x-x_i,C_i(x)=A(x)~mod~B_i(x)\),那么\(B_i(x_i)=0\)。所以\(A(x_i)=C_i(x_i)\)。但是计算\(B_i(x)\)和\(C_i(x)\)是\(O(n)\)的,必须加速这个过程。
设当前求值的点为\(X=\{x_0,x_1,\cdots,x_{n-1}\}\),我们可以把这\(n\)个点分为两半:
构造多项式
那么当\(x\in X_0\)时\(A(x)=A_0(x)\),可以递归计算。当\(x\in X_1\)时同理。
每一层计算\(B_0,B_1,A_0,A_1\)的时间复杂度都是\(O(n\log n)\)
总的时间复杂度就是
快速插值
考虑怎么求\(g_i=\prod_{j=0,j\neq i}^n (x_i-x_j)\),也就是分母。
可以分治求出\(\prod_{j=0}^n (x-x_j)\)再求导后在所有\(x_i\)处多点求值。
分子直接分治求出。
时间复杂度:\(O(n\log^2n)\)
小技巧1
比如我们要计算两个实数序列的卷积\(A\times B=C\),记\(D_i=(a_i+b_i)+(a_i-b_i)i\),那么\(C_i=\frac{1}{4}real({D^2}_i)\)。
这样就可以把三次DFT减少到两次DFT。
当然,如果\(A=B\)那么这个优化是没有效果的。
任意模数FFT
模板
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<utility>
#include<cmath>
#include<functional>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
void sort(int &a,int &b)
{
if(a>b)
swap(a,b);
}
void open(const char *s)
{
#ifndef ONLINE_JUDGE
char str[100];
sprintf(str,"%s.in",s);
freopen(str,"r",stdin);
sprintf(str,"%s.out",s);
freopen(str,"w",stdout);
#endif
}
int rd()
{
int s=0,c;
while((c=getchar())<'0'||c>'9');
do
{
s=s*10+c-'0';
}
while((c=getchar())>='0'&&c<='9');
return s;
}
int upmin(int &a,int b)
{
if(b<a)
{
a=b;
return 1;
}
return 0;
}
int upmax(int &a,int b)
{
if(b>a)
{
a=b;
return 1;
}
return 0;
}
const ll p=998244353;
const ll g=3;
ll fp(ll a,ll b)
{
ll s=1;
while(b)
{
if(b&1)
s=s*a%p;
a=a*a%p;
b>>=1;
}
return s;
}
const int maxn=600000;
ll inv[maxn];
namespace ntt
{
ll w1[maxn];
ll w2[maxn];
int rev[maxn];
int n;
void init(int m)
{
n=1;
while(n<m)
n<<=1;
int i;
for(i=2;i<=n;i<<=1)
{
w1[i]=fp(g,(p-1)/i);
w2[i]=fp(w1[i],p-2);
}
rev[0]=0;
for(i=1;i<n;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)*(n>>1));
}
void ntt(ll *a,int t)
{
int i,j,k;
ll u,v,w,wn;
for(i=0;i<n;i++)
if(rev[i]<i)
swap(a[i],a[rev[i]]);
for(i=2;i<=n;i<<=1)
{
wn=(t==1?w1[i]:w2[i]);
for(j=0;j<n;j+=i)
{
w=1;
for(k=j;k<j+i/2;k++)
{
u=a[k];
v=a[k+i/2]*w%p;
a[k]=(u+v)%p;
a[k+i/2]=(u-v)%p;
w=w*wn%p;
}
}
}
if(t==-1)
{
u=fp(n,p-2);
for(i=0;i<n;i++)
a[i]=a[i]*u%p;
}
}
ll x[maxn];
ll y[maxn];
ll z[maxn];
void copy_clear(ll *a,ll *b,int m)
{
int i;
for(i=0;i<m;i++)
a[i]=b[i];
for(i=m;i<n;i++)
a[i]=0;
}
void copy(ll *a,ll *b,int m)
{
int i;
for(i=0;i<m;i++)
a[i]=b[i];
}
void mul(ll *a,ll *b,ll *c,int m)
{
init(m<<1);
copy_clear(x,a,m);
copy_clear(y,b,m);
ntt(x,1);
ntt(y,1);
int i;
for(i=0;i<n;i++)
x[i]=x[i]*y[i]%p;
ntt(x,-1);
copy(c,x,m);
}
void inverse(ll *a,ll *b,int m)
{
if(m==1)
{
b[0]=fp(a[0],p-2);
return;
}
inverse(a,b,m>>1);
init(m<<1);
copy_clear(x,a,m);
copy_clear(y,b,m>>1);
ntt(x,1);
ntt(y,1);
int i;
for(i=0;i<n;i++)
x[i]=y[i]*(2-x[i]*y[i]%p)%p;
ntt(x,-1);
copy(b,x,m);
}
ll c[maxn],d[maxn],e[maxn],f[maxn];
void sqrt(ll *a,ll *b,int m)
{
if(m==1)
{
if(a[0]==1)
b[0]=1;
else if(a[0]==0)
b[0]=0;
else
//我也不会
;
return;
}
sqrt(a,b,m>>1);
// copy_clear(c,b,m>>1);
int i;
for(i=m;i<m<<1;i++)
b[i]=0;
inverse(b,d,m);
init(m<<1);
for(i=m;i<m<<1;i++)
b[i]=d[i]=0;
ll inv2=fp(2,p-2);
copy_clear(x,a,m);
ntt(x,1);
ntt(d,1);
for(i=0;i<n;i++)
x[i]=x[i]*d[i]%p;
ntt(x,-1);
for(i=0;i<m;i++)
b[i]=((b[i]+x[i])%p*inv2)%p;
}
void derivative(ll *a,ll *b,int m)
{
int i;
for(i=0;i<m-1;i++)
b[i]=(i+1)*a[i+1]%p;
b[m-1]=0;
}
void differential(ll *a,ll *b,int m)
{
int i;
for(i=m-1;i>=1;i--)
b[i]=a[i-1]*inv[i]%p;
b[0]=0;
}
void ln(ll *a,ll *b,int m)
{
static ll c[maxn],d[maxn];
derivative(a,c,m);
inverse(a,d,m);
init(m<<1);
int i;
for(i=m;i<n;i++)
c[i]=d[i]=0;
ntt(c,1);
ntt(d,1);
for(i=0;i<n;i++)
c[i]=c[i]*d[i]%p;
ntt(c,-1);
differential(c,b,m);
}
void exp(ll *a,ll *b,int m)
{
if(m==1)
{
b[0]=1;
return;
}
exp(a,b,m>>1);
int i;
for(i=m>>1;i<m;i++)
b[i]=0;
ln(b,y,m);
init(m<<1);
copy_clear(x,a,m);
x[0]++;
for(i=0;i<m;i++)
x[i]=(x[i]-y[i])%p;
copy_clear(y,b,m);
ntt(x,1);
ntt(y,1);
for(i=0;i<n;i++)
x[i]=x[i]*y[i]%p;
ntt(x,-1);
copy(b,x,m);
}
void module(ll *a,ll *b,ll *c,int n1,int n2)
{
int k=1;
while(k<=n1-n2+1)
k<<=1;
int i;
for(i=0;i<=n1;i++)
d[i]=a[i];
for(i=0;i<=n2;i++)
e[i]=b[i];
reverse(d,d+n1+1);
reverse(e,e+n2+1);
for(i=n1-n2+1;i<k<<1;i++)
d[i]=e[i]=0;
inverse(e,f,k);
for(i=n1-n2+1;i<k<<1;i++)
f[i]=0;
init(k<<1);
ntt::ntt(d,1);
ntt::ntt(f,1);
for(i=0;i<n;i++)
e[i]=d[i]*f[i]%p;
ntt::ntt(e,-1);
for(i=0;i<=n1-n2;i++)
c[i]=e[i];
reverse(c,c+n1-n2+1);
}
};
ll b[maxn];
ll a[maxn];
ll c[maxn];
void get(ll *a,int n)
{
int i;
for(i=0;i<n;i++)
a[i]=rand();
}
int main()
{
// freopen("fft.txt","w",stdout);
// srand(time(0));
// int n=262144;
// int bg,ed;
// int i;
// int times=100,j;
// double s,s1;
// inv[0]=inv[1]=1;
// for(i=2;i<=n;i++)
// inv[i]=-(p/i)*inv[p%i]%p;
// s=0;
// for(j=1;j<=times;j++)
// {
// get(a,n);
// bg=clock();
// ntt::init(n);
// ntt::ntt(a,1);
// ed=clock();
// s+=double(ed-bg)/CLOCKS_PER_SEC;
// }
// printf("ntt :%.10lf\n",s/times);
// s1=s;
// s=0;
// for(j=1;j<=times;j++)
// {
// get(a,n);
// get(b,n);
// bg=clock();
// ntt::mul(a,b,c,n);
// ed=clock();
// s+=double(ed-bg)/CLOCKS_PER_SEC;
// }
// printf("mul :%.10lf %.10lf\n",s/times,s/s1);
// s=0;
// for(j=1;j<=times;j++)
// {
// get(a,n);
// bg=clock();
// ntt::inverse(a,b,n);
// ed=clock();
// s+=double(ed-bg)/CLOCKS_PER_SEC;
// }
// printf("inv :%.10lf %.10lf\n",s/times,s/s1);
// s=0;
// for(j=1;j<=times;j++)
// {
// get(a,n);
// a[0]=1;
// bg=clock();
// ntt::sqrt(a,b,n);
// ed=clock();
// s+=double(ed-bg)/CLOCKS_PER_SEC;
// }
// printf("sqrt:%.10lf %.10lf\n",s/times,s/s1);
// s=0;
// for(j=1;j<=times;j++)
// {
// get(a,n);
// a[0]=1;
// bg=clock();
// ntt::ln(a,b,n);
// ed=clock();
// s+=double(ed-bg)/CLOCKS_PER_SEC;
// }
// printf("ln :%.10lf %.10lf\n",s/times,s/s1);
// s=0;
// for(j=1;j<=times;j++)
// {
// get(a,n);
// bg=clock();
// ntt::exp(a,b,n);
// ed=clock();
// s+=double(ed-bg)/CLOCKS_PER_SEC;
// }
// printf("exp :%.10lf %.10lf\n",s/times,s/s1);
// return 0;
}
多点求值+快速插值
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll p=998244353;
const ll g=3;
const int maxw=131072;
const int maxn=150000;
ll fp(ll a,ll b)
{
ll s=1;
for(;b;b>>=1,a=a*a%p)
if(b&1)
s=s*a%p;
return s;
}
int rt,cnt,ls[1000010],rs[1000010];
ll vx[100010],vy[100010],va[100010];
ll inv[maxn],w1[maxn],w2[maxn];
int rev[maxn];
void init()
{
inv[0]=inv[1]=1;
for(int i=2;i<=maxw;i++)
inv[i]=-p/i*inv[p%i]%p;
for(int i=2;i<=maxw;i<<=1)
{
w1[i]=fp(g,(p-1)/i);
w2[i]=fp(w1[i],p-2);
}
}
ll *f[1000010];
int len[maxn];
void clear(ll *a,int n)
{
memset(a,0,(sizeof a[0])*n);
}
void ntt(ll *a,int n,int t)
{
for(int i=1;i<n;i++)
{
rev[i]=(rev[i>>1]>>1)|(i&1?n>>1:0);
if(i>rev[i])
swap(a[i],a[rev[i]]);
}
for(int i=2;i<=n;i<<=1)
{
ll wn=(t==1?w1[i]:w2[i]);
for(int j=0;j<n;j+=i)
{
ll w=1;
for(int k=j;k<j+i/2;k++)
{
ll u=a[k];
ll v=a[k+i/2]*w%p;
a[k]=(u+v)%p;
a[k+i/2]=(u-v)%p;
w=w*wn%p;
}
}
}
if(t==-1)
{
ll inv=fp(n,p-2);
for(int i=0;i<n;i++)
a[i]=a[i]*inv%p;
}
}
void mul(ll *a,ll *b,ll *c,int n,int m)
{
int k=1;
while(k<=n+m)
k<<=1;
static ll a1[maxn],a2[maxn];
clear(a1,k);
clear(a2,k);
for(int i=0;i<=n;i++)
a1[i]=a[i];
for(int i=0;i<=m;i++)
a2[i]=b[i];
ntt(a1,k,1);
ntt(a2,k,1);
for(int i=0;i<k;i++)
a1[i]=a1[i]*a2[i]%p;
ntt(a1,k,-1);
for(int i=0;i<=n+m;i++)
c[i]=a1[i];
}
void getinv(ll *a,ll *b,int n)
{
if(n==1)
{
b[0]=fp(a[0],p-2);
return;
}
getinv(a,b,n>>1);
static ll a1[maxn],a2[maxn];
clear(a1,n<<1);
clear(a2,n<<1);
for(int i=0;i<n;i++)
a1[i]=a[i];
for(int i=0;i<n>>1;i++)
a2[i]=b[i];
ntt(a1,n<<1,1);
ntt(a2,n<<1,1);
for(int i=0;i<n<<1;i++)
a1[i]=a2[i]*(2-a2[i]*a1[i]%p)%p;
ntt(a1,n<<1,-1);
for(int i=0;i<n;i++)
b[i]=a1[i];
}
void div(ll *a,ll *b,ll *c,int n,int m)
{
static ll a1[maxn],a2[maxn],a3[maxn];
int k=1;
while(k<=2*(n-m))
k<<=1;
for(int i=0;i<=n;i++)
a1[i]=a[i];
for(int i=0;i<=m;i++)
a2[i]=b[i];
reverse(a1,a1+n+1);
reverse(a2,a2+m+1);
clear(a1+n-m+1,k-(n-m+1));
clear(a2+n-m+1,k-(n-m+1));
getinv(a2,a3,k);
clear(a3+n-m+1,k-(n-m+1));
ntt(a1,k,1);
ntt(a3,k,1);
for(int i=0;i<k;i++)
a1[i]=a1[i]*a3[i]%p;
ntt(a1,k,-1);
for(int i=0;i<=n-m;i++)
c[i]=a1[i];
reverse(c,c+n-m+1);
}
void getmod(ll *a,ll *b,ll *c,int n,int m)
{
static ll a1[maxn],a2[maxn];
int k=1;
while(k<=n)
k<<=1;
clear(a1,k);
clear(a2,k);
for(int i=0;i<=m;i++)
a1[i]=b[i];
div(a,b,a2,n,m);
ntt(a1,k,1);
ntt(a2,k,1);
for(int i=0;i<k;i++)
a1[i]=a1[i]*a2[i]%p;
ntt(a1,k,-1);
for(int i=0;i<m;i++)
c[i]=(a[i]-a1[i])%p;
}
void divide(int l,int r,int &now)
{
now=++cnt;
len[now]=r-l+1;
f[now]=new ll[len[now]+1];
if(l==r)
{
f[now][1]=1;
f[now][0]=-vx[l];
return;
}
int mid=(l+r)>>1;
divide(l,mid,ls[now]);
divide(mid+1,r,rs[now]);
mul(f[ls[now]],f[rs[now]],f[now],len[ls[now]],len[rs[now]]);
}
void getv(ll *a,int n,int l,int r,int now)
{
ll *a1=new ll[len[now]];
getmod(a,f[now],a1,n,len[now]);
if(l==r)
{
va[l]=a1[0];
return;
}
int mid=(l+r)>>1;
getv(a1,len[now]-1,l,mid,ls[now]);
getv(a1,len[now]-1,mid+1,r,rs[now]);
}
ll *s[1000010];
void getpoly(int l,int r,int now)
{
s[now]=new ll[len[now]];
if(l==r)
{
s[now][0]=va[l];
return;
}
int mid=(l+r)>>1;
getpoly(l,mid,ls[now]);
getpoly(mid+1,r,rs[now]);
int k=1;
while(k<=len[now])
k<<=1;
static ll a1[maxn],a2[maxn],a3[maxn],a4[maxn];
clear(a1,k);
clear(a2,k);
clear(a3,k);
clear(a4,k);
for(int i=0;i<len[ls[now]];i++)
a1[i]=s[ls[now]][i];
for(int i=0;i<=len[rs[now]];i++)
a2[i]=f[rs[now]][i];
for(int i=0;i<len[rs[now]];i++)
a3[i]=s[rs[now]][i];
for(int i=0;i<=len[ls[now]];i++)
a4[i]=f[ls[now]][i];
ntt(a1,k,1);
ntt(a2,k,1);
ntt(a3,k,1);
ntt(a4,k,1);
for(int i=0;i<k;i++)
a1[i]=(a1[i]*a2[i]+a3[i]*a4[i])%p;
ntt(a1,k,-1);
for(int i=0;i<len[now];i++)
s[now][i]=a1[i];
}
int n;
ll a[maxn],b[maxn],c[maxn];
int main()
{
init();
scanf("%d",&n);
for(int i=0;i<=n;i++)
scanf("%lld%lld",&vx[i],&vy[i]);
divide(0,n,rt);
for(int i=0;i<=n;i++)
a[i]=f[rt][i+1]*(i+1)%p;
getv(a,n,0,n,rt);
// for(int i=0;i<=n;i++)
// printf("%lld ",(va[i]+p)%p);
// printf("\n");
for(int i=0;i<=n;i++)
va[i]=fp(va[i],p-2)*vy[i]%p;
getpoly(0,n,rt);
for(int i=0;i<=n;i++)
printf("%lld ",(s[rt][i]+p)%p);
printf("\n");
return 0;
}








 浙公网安备 33010602011771号
浙公网安备 33010602011771号