POJ1179 Polygon

 

描述

Polygon是一个玩家的游戏，它从具有N个顶点的多边形开始，如图1所示，其中N = 4。每个顶点用整数标记，每个边用标记+（加法）或符号*（产品）标记。边缘编号从1到N. 

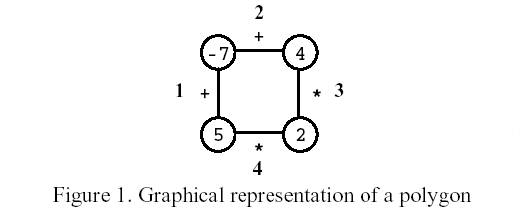
在第一步中，其中一条边被移除。后续移动包括以下步骤： 
挑边E和由E链接的两个顶点V1和V2; 并且 
用新的顶点替换它们，标记为在V1和V2的标签上执行E中指示的操作的结果。 
当没有更多边缘时游戏结束，并且其得分是剩余的单个顶点的标签。 

考虑图1中的多边形。玩家通过移除边缘3开始。之后，玩家选择边缘1，然后是边缘4，最后是边缘2.分数为0。 

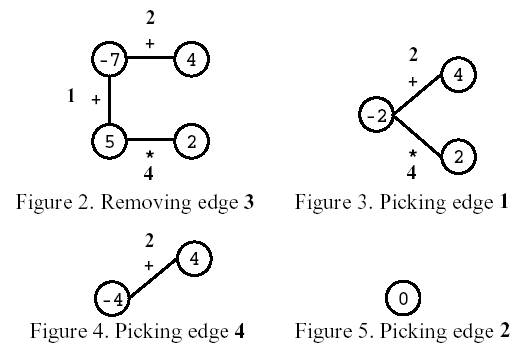
编写一个程序，给定一个多边形，计算最高分数并列出所有边缘，如果在第一步移动，可以导致具有该分数的游戏。 

输入

您的程序是从标准输入读取。输入描述具有N个顶点的多边形。它包含两行。在第一行是数字N.第二行包含边缘1，...，N的标签，与顶点的标签交织（首先是边缘1和2之间的顶点，然后是边缘之间的顶点）在图2和图3中，依此类推，直到边缘N和1之间的顶点之间，全部由一个空间隔开。边标签是字母t（表示+）或字母x（表示*）。 

3 <= N <= 50 
对于任何移动序列，顶点标签都在[-32768,32767]范围内。 

产量

你的程序是写入标准输出。在第一行，您的程序必须写入输入多边形可以获得的最高分数。在第二行，它必须写出所有边缘的列表，如果在第一步移除，则可以导致具有该分数的游戏。边缘必须按递增顺序书写，以一个空格分隔。

样本输入

4
t -7 t 4 x 2 x 5

样本输出

33
1 2

在枚举哪一条边删除过后，这道题就与“石子合并非常相似了”，仍然是在每一步中对两个端点做某种运算将他们合并。简便起见，我们把被删除的边逆时针方向的顶点称为“第一个顶点”，依此类推。容易想到，用f[l,r]表示第l到第r个顶点合成一个顶点后，顶点的最大数值是多少。
如果这道题的顶点全为正数，我们已经A了这道题了
我们先来看看动态规划的三个前提：
“子问题重叠性”“无后效性”和“最优子结构”
什么是最优子结构呢？
搬用算法导论的话：“如果一个问题的最优解包含其子问题的最优解，我们就称此问题具有最优子结构。”
我们再看看这道题是否满足
事实上，最优子结构不再满足了。
因为负数的存在，在由小区间向大区间合并时，大区间[l,r]合成的顶点的最大值无法由[l,k]和[k+1,r]导出，因为[l,k]和[k+1,r]合成的两个顶点的最小数值可能是很小的负数，但如果符号为乘号，负负得正，运算的结果可能会变得更大
那么我们想一想问题怎么解决。
如果我们把区间[l,r]合并的最小值和最大值同时作为子问题[l,r]的代表信息，就可以满足最优子结构了。最大值的来源只可能是两个最大值相加、相乘或两个最小值相乘（负负得正），这是很显然的，若两个最大值都是正数，合并后，自然是相乘或是相加，但是两个最小值都是负数并且特别小，他们的乘积就会很大，所以有这3种可能来源。
而[l,r]合并后的最小值，来源只可能是两个最小值想加、相乘，或一个最大值与一个最小值相乘（正负得负），这也是很显然的，不再赘述。

因此，可以设f[l,r,0]表示第l到r顶点合成一个顶点后的最大值，f[l,r,1]表式第l到r顶点合成一个顶点后的最小值是多少，枚举区间划分点k决策，然后我们就可以仿照合并石头写出状态转移方程,op表示符号
f[l,r,0] = max{f[l,k,0] op f[k+1,r,0]}
{f[l,k,1] op f[k+1,r,1](若op为乘号)}
f[l,r,1] = min{f[l,k,1] op f[k+1,r,1]}
min{f[l,k,1] op f[k+1,r,0], f[l,k,1] op f[k+1,r,1]}(若op为乘号)
初态: f[l,l,0] = f[l,l,1] = Al,其余均为正或负无穷
目标: f[1,n,0]
但是在实际写题的时候还是需要考虑循环的东西....emmmm.

以上算法是O(n^4)的，因为在上述算法中，除了基本的三重循坏外，我们还需要枚举删除哪一条边
但实际我们是可以把这个优化掉的，我们先这样想，比如：
1 3 -7 8
这样一个环
我们设1和3之间是+号，我们删掉[1,3]后，原序列变为
4 -7 8
我们会发现，序列长度减小了，也就是说我们只能算先删掉[1,3]这一种情况了，那么我们要怎么办？
我们把这个序列再复制一次接在原序列后面看看
4 -7 8 4 -7 8
我们再看看是否能够完成我们刚才所说的问题
答案是能，
[1,3][2,4][3,5]这些都是与原来等效的，我们如此处理后，就可以一次枚举所有情况而不用枚举每次删掉哪一条边
然后再想，如果最初的[1,3]不进行合并，直接复制一次呢？
1 3 -7 8 1 3 -7 8
我们就能发现，可行，这样我们就省去了枚举断边的问题
我们原本枚举断掉第i条边的问题就可以对应为[i, i + n]
[i, i + n]就可以描述先断掉第i条边合并第i条边连接的两点，复杂度就降低为O(n^3)了
从这个问题我们可以总结出一条规律性结论：
对于动态归划的环形问题，“任意选择一个位置断开，复制形成2倍长度的链”是解决环形问题的常用手段之一。
其表现为，将链的长度扩为2*n,对于一个序列a,a[i+n] = a[i]

 

 重写了一遍后感觉，以前说这道题不好写的我，还是太年轻.....

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<ctime>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#define ll long long
#define uint unsigned int
#define ull unsigned long long
using namespace std;
const int maxn = 200;
int f_max[maxn][maxn], f_min[maxn][maxn];//最大值，最小值
int a[maxn], coa[maxn], ans = -2e9; 
int cut[maxn], tot = 0;
char ch;
int n; 

inline int read() {
    int x = 0, y = 1;
    char ch = getchar();
    while(!isdigit(ch)) {
        if(ch == '-') y = -1;
        ch = getchar();
    }
    while(isdigit(ch)) {
        x = (x << 1) + (x << 3) + ch - '0';
        ch = getchar();
    }
    return x * y;
}

inline int break_this_line(int x) {
    memset(f_max, 0xcf, sizeof(f_max));
    memset(f_min, 0x3f, sizeof(f_min));
    for(int i = 1; i <= x + n - 1; ++i) 
        f_max[i][i] = f_min[i][i] = a[i];
    for(int len = 1; len <= n; ++len) 
        for(int l = x; l + len - 1 <= x + n - 1; ++l) {
            int r = l + len - 1;
            for(int k = l + 1; k <= r; ++k) {
                if(coa[k]) {
                    f_max[l][r] = max(f_max[l][r], f_max[l][k - 1] * f_max[k][r]);
                    f_max[l][r] = max(f_max[l][r], f_min[l][k - 1] * f_min[k][r]);
                    f_min[l][r] = min(f_min[l][r], f_max[l][k - 1] * f_min[k][r]);
                    f_min[l][r] = min(f_min[l][r], f_min[l][k - 1] * f_min[k][r]);
                    f_min[l][r] = min(f_min[l][r], f_min[l][k - 1] * f_max[k][r]);
                }
                else if(!coa[k]) {
                    f_max[l][r] = max(f_max[l][r], f_max[l][k - 1] + f_max[k][r]);
                    f_min[l][r] = min(f_min[l][r], f_min[l][k - 1] + f_min[k][r]);
                }
            }
        } 
    return f_max[x][x + n - 1];
}

int main() {
    memset(coa, -1, sizeof(coa));
    n = read();
    for(int i = 1; i <= n; ++i) {
        cin >> ch; a[i] = read();
        if(ch == 'x') coa[i + n] = coa[i] = 1;
        else coa[i + n] = coa[i] = 0;
        a[i + n] = a[i];
    }
    for(int i = 1; i <= n; ++i) {
        int now = break_this_line(i);
        if(ans == now) cut[++tot] = i;
        else if(ans < now) ans = now, cut[tot = 1] = i;
    }
    printf("%d\n", ans);
    for(int i = 1; i <= tot; ++i)
        printf("%d ", cut[i]);
    printf("\n");
    return 0;
}