2-SAT 问题の笔记

定义

有 \(m\) 个限制，每一个限制中有 2 个元素，表示 2 个元素的布尔值关系。

问是否有解与解是什么

思路

将一个元素视为两个点 \(x,\ !x\)。

对于一个限制 \(x,\ y\)，连两条边：

• \(x\to\ !y\)
• \(y\to\ !x\)

如果存在 \(x,\ !x\) 在同一个 SCC 中，则无解。

如果有解，对于一个元素 \(x\)，取 scc[x] 与 scc[!x] 中小的为答案

步骤

1. 根据条件建有向图
2. Tarjan 求 SCC 编号
3. 枚举判断是否有解
4. 若有解，枚举构造

时间复杂度

\(O(m+n)\)
其中 \(m\) 为限制个数，\(n\) 为元素个数。

例题

• P4782 【模板】2-SAT

限制：元素 \(x\) 为真/假 或 元素 \(y\) 为真/假，及至少有一个成立。

对于一个限制 \(x,\ y\)，连两条边：

• \(!x\to\ y\)
• \(!y\to\ x\)

#include<bits/stdc++.h>
using namespace std;
int tim, scccnt;
vector<int> G[2000005];
int scc[2000005], low[2000005], dfn[2000005];
stack<int> st;
void tarjan(int u)
{
	low[u] = dfn[u] = ++ tim;
	st.push(u);
	for(int i = 0; i < G[u].size(); i ++)
	{
		int v = G[u][i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		else if(!scc[v])
		{
			low[u] = min(low[u], dfn[v]);
		}
	}
	if(low[u] == dfn[u])
	{
		scccnt ++;
		int U;
		do
		{
			U = st.top();
			st.pop();
			scc[U] = scccnt;
		}while(U != u);
	}
}
signed main()//i:true i+n:false
{
	int n, m, x, y;
	bool a, b;
	cin >> n >> m;
	for(int i = 1; i <= m; i ++)
	{
		cin >> x >> a >> y >> b;
		G[x + (n * a)].push_back(y + n - (n * b));
		G[y + (n * b)].push_back(x + n - (n * a));
	}
	for(int i = 1; i <= 2 * n; i ++)
	{
		if(!scc[i])
		{
			tarjan(i);
		}
	}
	for(int i = 1; i <= n; i ++)
	{
		if(scc[i] == scc[i + n])
		{
			cout << "IMPOSSIBLE";
			return 0;
		}
	}
	cout << "POSSIBLE" << endl;
	for(int i = 1; i <= n; i ++)
	{
		cout << (scc[i] < scc[i + n]) << ' ';
	}
	return 0;
}

---

• P6378 [PA 2010] Riddle

限制：元素 \(x\) 为真/假 或 元素 \(y\) 为真/假，及至少有一个成立 + 一组多个元素中最多只有一个为真。

对于一个限制 \(x,\ y\)，连两条边：

• \(!x\to\ y\)
• \(!y\to\ x\)

对于一个多元素限制，多开一些点，连成这样：

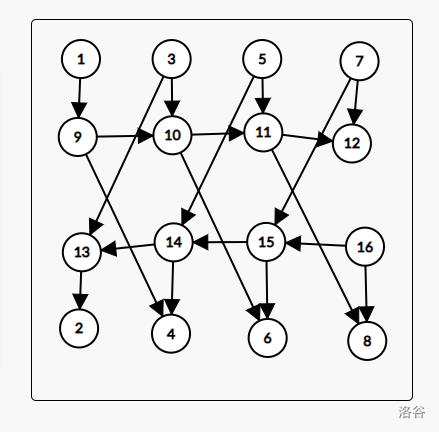
(Picture From: @阴阳八卦's Solution)

其中第一排为元素为 真 的点，第二排为元素为 假 的点，第二、三排点为额外加的点，此图与暴力 \(O(n^2)\) 加边的图等价。

连边时间复杂度降为：\(O(n)\)

#include<bits/stdc++.h>
using namespace std;
int tim, scccnt;
vector<int> G[4000005];
int scc[4000005], low[4000005], dfn[4000005];
stack<int> st;
void tarjan(int u)
{
	low[u] = dfn[u] = ++ tim;
	st.push(u);
	for(int i = 0; i < G[u].size(); i ++)
	{
		int v = G[u][i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		else if(!scc[v])
		{
			low[u] = min(low[u], dfn[v]);
		}
	}
	if(low[u] == dfn[u])
	{
		scccnt ++;
		int U;
		do
		{
			U = st.top();
			st.pop();
			scc[U] = scccnt;
		}while(U != u);
	}
}
int a[1000005], pre[2000005][2];
signed main()//i:true i+n:false
{
	int n, m, k, x, y;
	cin >> n >> m >> k;
	for(int i = 1; i <= m; i ++)
	{
		cin >> x >> y;
		G[x + n].push_back(y);
		G[y + n].push_back(x);
	}
	int id = 2 * n;
	for(int _ = 1; _ <= k; _ ++)
	{
		int w;
		cin >> w;
		for(int i = 1; i <= w; i ++)
		{
			cin >> a[i];
			pre[a[i]][0] = ++ id;
			pre[a[i]][1] = ++ id;
			G[a[i]].push_back(pre[a[i]][0]);
			G[pre[a[i]][1]].push_back(a[i] + n);
		}
		for(int i = 2; i <= w; i ++)
		{
			G[pre[a[i - 1]][0]].push_back(pre[a[i]][0]);
			G[pre[a[i]][1]].push_back(pre[a[i - 1]][1]);
			G[a[i]].push_back(pre[a[i - 1]][1]);
			G[pre[a[i - 1]][0]].push_back(a[i] + n);
		}
	}
	for(int i = 1; i <= 4 * n; i ++)
	{
		if(!scc[i])
		{
			tarjan(i);
		}
	}
	for(int i = 1; i <= n; i ++)
	{
		if(scc[i] == scc[i + n])
		{
			cout << "NIE";
			return 0;
		}
	}
	cout << "TAK";
	return 0;
}