爱思创 180611 矩形 题解

180611 矩形

思路1：枚举

枚举每一个点，包括左上角x、y、右下角x、y、边框上每一个点：五重循环
\(O(n^5)\)
但一看到范围

n<=300

别想了 走吧，这里没东西了

那能不能优化呢？
看一看问题在哪儿

包括左上角x、y、右下角x、y、边框上每一个点：五重循环

左上角x、y、右下角x、y肯定不能省，那就你吧：边框上每一个点

思路2：前缀和优化

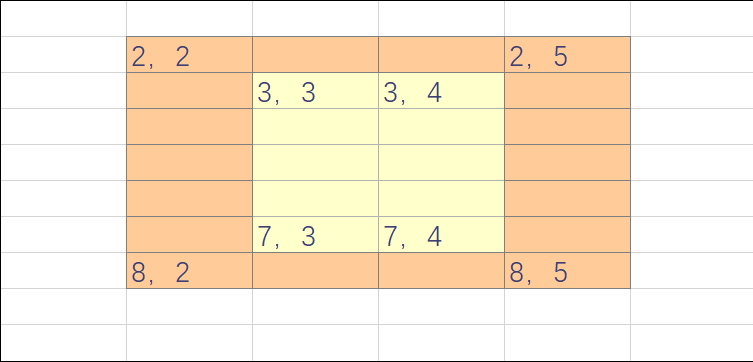
我们用二维前缀和做优化
\(O(n^4)\)

如何使用前缀和求解

请看图
要求一个矩形边上的点数，实际就是整个矩形里包含的点数 \(-\) 里面一层矩形包含的点数
用前缀和数组表示就是(s[k][l] + s[i - 1][j - 1] - s[i - 1][l] - s[k][j - 1]) - (s[k - 1][l - 1] + s[i][j] - s[i][l - 1] - s[k - 1][j])

正确步骤

1.输入：哪个位置有点，标为1

2.预处理：用前缀和

3.枚举：求解答案

---

我们主要说一下第三点：

先写两层循环枚举左上点的 x, y 坐标
再写两层循环枚举右下点的 x, y 坐标
右下点的范围是 \(\color{purple}{\text{左上点 + 1} \leq 右下点 \leq 100}\)
最后算最大值

完整代码

#include<bits/stdc++.h>
using namespace std;
int s[305][305];
int a[305][305];
int main()
{
    int n, x, y;
    cin >> n;
    for(int i = 1; i <= n; i ++)
    {
        cin >> x >> y;
        a[x][y] = 1;
    }
    for(int i = 1; i <= 100; i ++)
    {
        for(int j = 1; j <= 100; j ++)
        {
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }
    int ans = 0;
    for(int i = 1; i <= 99; i ++)
    {
        for(int j = 1; j <= 99; j ++)
        {
            for(int k = i + 1; k <= 100; k ++)
            {
                for(int l = j + 1; l <= 100; l ++)
                {
                    ans = max(ans, (s[k][l] + s[i - 1][j - 1] - s[i - 1][l] - s[k][j - 1]) - (s[k - 1][l - 1] + s[i][j] - s[i][l - 1] - s[k - 1][j]));
                }
            }
        }
    }
    cout << ans;
    cout << "防复制代码，请勿复制！";
    cout << "防复制代码，请勿复制！";
    cout << "防复制代码，请勿复制！";
    return 0;
}