柔性直流输电控制原理

|| 本连载文章主要目标人群是正在或将要从事柔性直流输电研究工作的博士和硕士研究生、科研人员，希望能够加速研究生和科研人员了解柔性直流输电换流器（模块化多电*换流器）的相关背景知识。同时，也非常欢迎指出我文章当中阐述错误或不当之处，我将尽快修改。

|| 文章对于电气工程基础理论（如基本概念、电路原理、电机学、电磁场原理、电力电子技术基础等）的解释较少。如有此类问题，可下方留言或私信我询问。

|| 如果你看了这篇文章有所收获，记得点赞关注收藏。

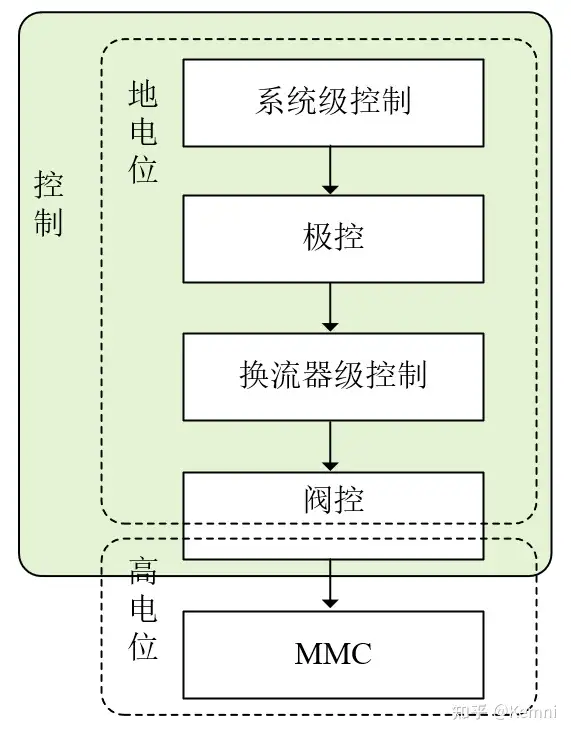
总地来看，柔性直流输电控制可以分为四层，分别是系统级控制、极控制（极控）、换流器级控制和换流阀控制（阀控）。不同级别之间的界限清晰，并通过通信系统连接。系统级控制主要决定直流系统的工作状态、运行模式、传输功率等。极控主要是针对每个输电极有多个MMC的情况所设置的控制级。如果每个输电极只有一台MMC，那么可以不设置独立的极控级。换流器级控制的主要作用是基于功率、电压参考值控制电流，输出桥臂调制波。阀控则是根据桥臂调制波、电容电压排序结果、桥臂电流方向等物理量，生成子模块半导体开关控制信号，从而控制桥臂输出电压，同时起到隔离高电位和地电位的作用。系统级控制、极控、换流器级控制都发生在地电位。阀控的一部分发生在地电位、一部分发生在高电位。本文主要讲解换流器级控制和阀控，同时涉及部分系统级控制的讲解。

图1 MMC控制层级

一、运行模式（系统级控制的一部分）

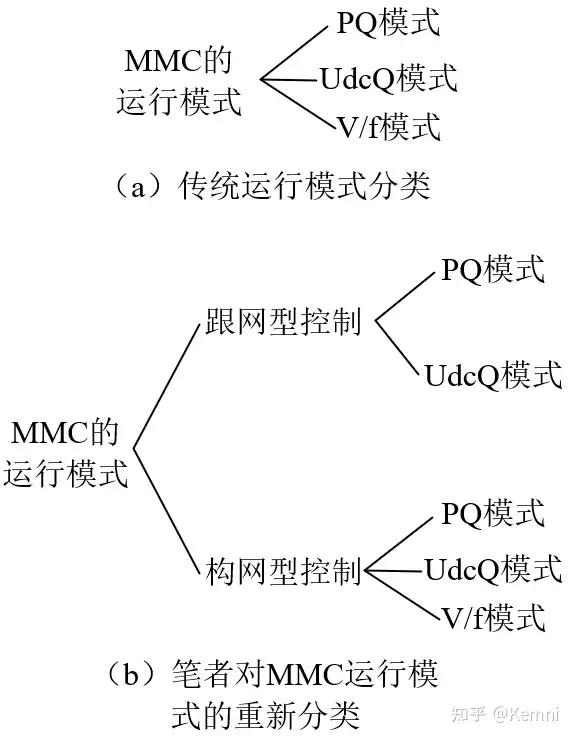
传统上讲，MMC的控制模式分为有功-无功模式（PQ模式）、直流电压-无功模式（UdcQ模式）和电压/频率模式（V/f模式），如图2（a）所示。

对于一个基于MMC的点对点直流输电系统，如果两台MMC都与电网连接，那么两台MMC中应当有一台控制直流电压，保证直流电压与参考值相同；而另一台MMC控制传输功率，使传输功率与调度指令相同。通常情况下由受端MMC控制系统直流电压、由送端MMC控制功率，即通常所说的“受端控电压、送端控功率”。但是，这也不是绝对的，也存在“送端控电压、受端控功率”的情况。除此之外，MMC还有一个无功控制维度。一类方式是直接控制交流侧与电网交换的无功功率的大小；另一类方式是利用无功功率交换能力起到支撑电网电压的作用。通常，与电网连接的MMC的控制模式通常分为PQ和UdcQ控制模式，只把有功控制维度分为有功功率和直流电压两种，而不对无功控制维度单独分类。MMC的V/f模式主要应用于柔性直流为无源网络供电的场景，基本原理是MMC控制交流电压的幅值和频率。

随着电力系统的不断发展，换流器的构网型控制被提出。在笔者看来，MMC的控制模式应当重新分类和归并，如图2（b）所示。MMC稳态运行模式可以分为跟网型控制和构网型控制，二者的根本区别是电压相位的获取方式不同。跟网型控制必须通过某种方式（通常为锁相环）得到电网电压相位，基于电网电压相位完成控制；构网型控制的电压相位则是控制器自身通过控制环节生成的。与跟网型控制相比，构网型控制最大的优势是更适合于弱电网。然而，考虑到跟网型控制的研究和应用更加成熟，本文主要阐述跟网型控制。

图2 MMC的运行模式

二、经典的换流器级控制

到目前为止，已经有许多学者针对换流器级控制进行了研究，主要可以分为经典控制和解耦控制两类。其中，经典的MMC换流器级控制继承自两电*电压源型换流器的控制，与两电*电压源型换流器的控制基本相同。经典的换流器级控制的优势是结构简单、易于理解、易于从两电*换流器的控制器继承；缺点是电流控制效果（尤其是快速性方面）不如解耦控制更好。解耦控制是专门针对MMC的一种控制方法。基于解耦控制理论，交流电流和直流电流可以不被交直流功率耦合在一起，从而实现解耦，电流控制效果得到大幅提升。但是，解耦控制的实现过程更加复杂。为了便于理解，本文仍阐述经典的MMC换流器级控制。解耦控制理论将在之后的文章中进行详细阐述。

经典的MMC换流器级控制主要分为内环电流控制器和外环电压/功率控制器。

1、内环电流控制器

以A相为例，根据上一篇文章，A相交流通路的数学模型为：

$u_{p\mathrm{\_}a}=-u_a+(L_T+\frac{L_0}{2})\frac{d{i}_a}{dt}$u_{p\_a}=-u_{a}+\left(L_T+\frac{L_0}{2}\right)\frac{di_{a}}{dt} ------（1）

$u_{n\mathrm{\_}a}=u_a-(L_T+\frac{L_0}{2})\frac{d{i}_a}{dt}$u_{n\_a}=u_{a}-\left(L_T+\frac{L_0}{2}\right)\frac{di_{a}}{dt} ------（2）

其中， $u_{p\mathrm{\_}a}、u_{n\mathrm{\_}a}$u_{p\_a}、u_{n\_a} 分别表示A相上、下桥臂电压的交流分量， $u_a$u_a 表示A相电网电压（折合到换流变阀侧）， $L_T、L_0$L_T、L_0 分别表示换流变漏感（折合到换流变阀侧）和桥臂电感值， $i_a$i_a 表示A相电流。上面两个方程本质上是同一个方程，即：

$L_{ac}\frac{d{i}_a}{dt}=u_a-e_a$L_{ac}\frac{di_a}{dt}=u_a-e_a ------（3）

其中， $L_{ac}=L_T+\frac{L_0}{2}$L_{ac}=L_T+\frac{L_0}{2} 是交流等效电感值， $u_{n\mathrm{\_}a}=e_a$u_{n\_a}=e_a ， $u_{p\mathrm{\_}a}=-e_a$u_{p\_a}=-e_a，而 $e_a$e_a 表示MMC的A相交流端口等效电压。因此，对于三相MMC来说，交流侧数学模型为：

$L_{ac}\frac{d}{dt}\left(\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right)=\left(\begin{array}{c}{u}_a\\ u_b\\ u_c\end{array}\right)-\left(\begin{array}{c}{e}_a\\ e_b\\ e_c\end{array}\right)$L_{ac}\frac{d}{dt} \left ( \begin{matrix} i_a\\ i_b\\ i_c\\ \end{matrix} \right ) = \left ( \begin{matrix} u_a\\ u_b\\ u_c\\ \end{matrix} \right ) - \left ( \begin{matrix} e_a\\ e_b\\ e_c\\ \end{matrix} \right ) ------（4）

其中，角标a、b、c分别表示三相。矩阵形式表达公式（4）如下：

$L_{ac}{\mathbf{I}}_{\mathbf{a}\mathbf{b}\mathbf{c}}^{\prime }={\mathbf{U}}_{\mathbf{a}\mathbf{b}\mathbf{c}}-{\mathbf{E}}_{\mathbf{a}\mathbf{b}\mathbf{c}}$L_{ac}\bold{I'_{abc}}=\bold{U_{abc}}-\bold{E_{abc}} ------（5）

其中，撇号表示变量对时间求导。上述方程基于abc坐标系已经可以清楚地描述MMC交流测等效数学模型。然而，公式（5）表达的MMC交流侧数学模型中，各变量均为工频正弦量。

PI控制器是一类原理简单、硬件实现方便的控制器，在工程领域有着广泛的应用。但是PI控制器在工频处的增益不是无穷大，所以对于工频正弦量的控制准确性较差。虽然也有研究提出比例谐振控制器，其特点是在给定频率（通常为工频）处的增益很大，但是真正的比例谐振控制器很难在硬件中实现，且谐振环节还可能带来一些震荡问题。因此，PI控制器仍然是电力电子领域最受青睐的控制器之一。Park变换可以将abc坐标系下的三相正弦量变为dq0坐标系下的三个直流量（严格来说是Park变换与Clark变换共同作用，将正弦量变为直流量），从而可以方便地利用PI控制器对其控制。Park变换矩阵为：

$\mathbf{P}=\frac{2}{3}\left(\begin{array}{ccc}cos(\omega t)& cos(\omega t-\frac{2\pi }{3})& cos(\omega t+\frac{2\pi }{3})\\ -sin(\omega t)& -sin(\omega t-\frac{2\pi }{3})& -sin(\omega t+\frac{2\pi }{3})\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right)$\bold{P}=\frac{2}{3} \left ( \begin{matrix} cos(\omega t) & cos(\omega t-\frac{2\pi}{3}) & cos(\omega t+\frac{2\pi}{3})\\ -sin(\omega t) & -sin(\omega t-\frac{2\pi}{3}) & -sin(\omega t+\frac{2\pi}{3})\\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \end{matrix} \right ) ------（6）

在公式（5）两端同乘 $\mathbf{P}$\bold{P} 矩阵，可得：

$$\begin{gathered} L_{ac}\mathbf{P}{\mathbf{I}}_{\mathbf{a}\mathbf{b}\mathbf{c}}^{\prime }=\mathbf{P}{\mathbf{U}}_{\mathbf{a}\mathbf{b}\mathbf{c}}-\mathbf{P}{\mathbf{E}}_{\mathbf{a}\mathbf{b}\mathbf{c}} \\ 即L_{ac}[\mathbf{(}\mathbf{P}{\mathbf{I}}_{\mathbf{a}\mathbf{b}\mathbf{c}}{\mathbf{)}}^{\prime }-{\mathbf{P}}^{\prime }{\mathbf{I}}_{\mathbf{a}\mathbf{b}\mathbf{c}}]={\mathbf{U}}_{\mathbf{d}\mathbf{q}\mathbf{0}}-{\mathbf{E}}_{\mathbf{d}\mathbf{q}\mathbf{0}} \\ 即L_{ac}{\mathbf{I}}_{\mathbf{d}\mathbf{q}\mathbf{0}}^{\prime }-L_{ac}{\mathbf{P}}^{\prime }{\mathbf{P}}^{\mathbf{-}\mathbf{1}}{\mathbf{I}}_{\mathbf{d}\mathbf{q}\mathbf{0}}={\mathbf{U}}_{\mathbf{d}\mathbf{q}\mathbf{0}}-{\mathbf{E}}_{\mathbf{d}\mathbf{q}\mathbf{0}} \end{gathered}$$L_{ac}\bold{P}\bold{I'_{abc}}=\bold{P}\bold{U_{abc}}-\bold{P}\bold{E_{abc}} \\ 即L_{ac}\left[\bold{(PI_{abc})'} - \bold{P'}\bold{I_{abc}} \right]=\bold{U_{dq0}}-\bold{E_{dq0}} \\ 即L_{ac} \bold{I'_{dq0}}-L_{ac}\bold{P'}\bold{P^{-1}}\bold{I_{dq0}}=\bold{U_{dq0}}-\bold{E_{dq0}} ------（7）

其中，

${\mathbf{P}}^{\prime }=\frac{2}{3}\omega \left(\begin{array}{ccc}-sin(\omega t)& -sin(\omega t-\frac{2\pi }{3})& -sin(\omega t+\frac{2\pi }{3})\\ -cos(\omega t)& -cos(\omega t-\frac{2\pi }{3})& -cos(\omega t+\frac{2\pi }{3})\\ 0& 0& 0\end{array}\right)$\bold{P'}=\frac{2}{3}\omega \left ( \begin{matrix} -sin(\omega t) & -sin(\omega t-\frac{2\pi}{3}) & -sin(\omega t+\frac{2\pi}{3})\\ -cos(\omega t) & -cos(\omega t-\frac{2\pi}{3}) & -cos(\omega t+\frac{2\pi}{3})\\ 0 & 0 & 0 \\ \end{matrix} \right ) ------（8）

${\mathbf{P}}^{\mathbf{-}\mathbf{1}}=\left(\begin{array}{ccc}cos(\omega t)& -sin(\omega t)& 1\\ cos(\omega t-\frac{2\pi }{3})& -sin(\omega t-\frac{2\pi }{3})& 1\\ cos(\omega t+\frac{2\pi }{3})& -sin(\omega t+\frac{2\pi }{3})& 1\end{array}\right)$\bold{P^{-1}}= \left ( \begin{matrix} cos(\omega t) & -sin(\omega t) & 1\\ cos(\omega t-\frac{2\pi}{3}) & -sin(\omega t-\frac{2\pi}{3}) & 1\\ cos(\omega t+\frac{2\pi}{3}) & -sin(\omega t+\frac{2\pi}{3}) & 1 \\ \end{matrix} \right ) ------（9）

因此， ${\mathbf{P}}^{\prime }{\mathbf{P}}^{\mathbf{-}\mathbf{1}}=\left(\begin{array}{ccc}0& \omega & 0\\ -\omega & 0& 0\\ 0& 0& 0\end{array}\right)$\bold{P'P^{-1}}=\left ( \begin{matrix} 0 & \omega & 0\\ -\omega & 0 & 0\\ 0 & 0 & 0 \\ \end{matrix} \right ) ------（10）

整理公式（7）可得

$L_{ac}\frac{d}{dt}\left(\begin{array}{c}{i}_d\\ i_q\\ i_0\end{array}\right)=\left(\begin{array}{c}{u}_d\\ u_q\\ u_0\end{array}\right)-\left(\begin{array}{c}{e}_d\\ e_q\\ e_0\end{array}\right)+\left(\begin{array}{c}\omega L_{ac}{i}_q\\ -\omega L_{ac}{i}_d\\ 0\end{array}\right)$L_{ac}\frac{d}{dt}\left ( \begin{matrix} i_d\\ i_q\\ i_0\\ \end{matrix} \right ) = \left ( \begin{matrix} u_d\\ u_q\\ u_0\\ \end{matrix} \right ) -\left ( \begin{matrix} e_d\\ e_q\\ e_0\\ \end{matrix} \right ) +\left ( \begin{matrix} \omega L_{ac}i_q\\ -\omega L_{ac}i_d\\ 0\\ \end{matrix} \right ) ------（11）

根据dq0坐标系下的MMC交流测数学模型，可以得到三相交流电流控制框图为：

图3 dq0坐标系下三相交流电流控制框图

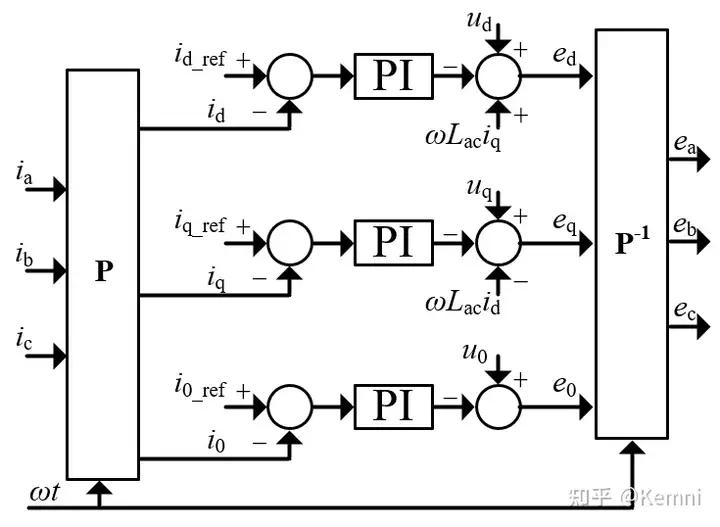
需要注意的是，许多教材或论文中不考虑0轴电流控制，这是因为在直流系统的设计阶段，许多工程并不允许零序电流流通（0轴电流与零序电流本质上是同一个物理量），因此无需控制0轴电流，只需考虑d和q轴即可。但是学者需要理解：如果系统的设计允许零序电流流通，那么说明abc三相电流是非线性相关的（即三相电流之和可以不为0），控制维度为3，那么在经过Park变换之后也必须考虑0轴电流才能保证控制维度不变。如果系统设计不允许零序电流流通，那么abc三相电流之和必为0，说明abc三相电流是线性相关的，本质上只有两个控制维度。那么，在Park变换之后也只需要考虑d和q两个轴的电流。

2、外环电压/功率控制器

电压/功率控制器指的是：如果MMC运行在UdcQ模式，则d轴外环为直流电压控制、q轴外环为无功功率控制；如果MMC运行在PQ模式，则d轴外环为有功功率控制、q轴外环为无功功率控制。

（1）UdcQ模式的电压环和功率环

图4 MMC直流侧等效电路

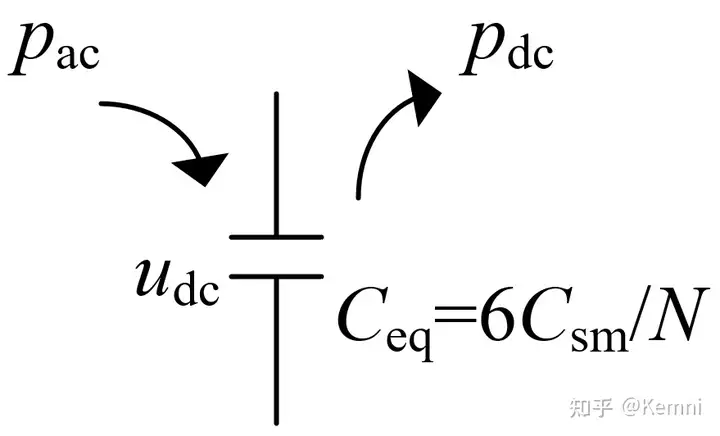
根据MMC直流侧等效电路，可以得到功率*衡方程：

$\frac{1}{2}{C}_{eq}\frac{d{u}_{dc}^2}{dt}=p_{ac}-p_{dc}=\frac{3}{2}{u}_d{i}_d-p_{dc}$\frac{1}{2}C_{eq}\frac{du_{dc}^2}{dt}=p_{ac}-p_{dc}=\frac{3}{2}u_di_d-p_{dc} ------（12）

其中， $p_{ac}、p_{dc}$p_{ac}、p_{dc} 分别表示交流有功功率和直流功率， $u_{dc}、u_d、i_d$u_{dc}、u_d、i_d 分别表示直流电压、交流d轴电压和d轴电流， $C_{eq}$C_{eq} 表示MMC的直流等效电容， $C_{sm}$C_{sm} 表示子模块电容值，N表示桥臂子模块数。对于MMC直流等效电容的理解请参考本篇文章第四节。基于公式（2）可以得到直流电压的控制框图为：

图5 基于功率*衡方程得到的直流电压外环控制器

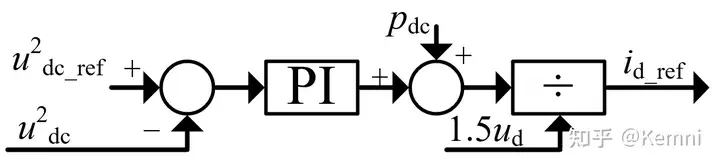
基于功率*衡方程得到的直流电压外环控制器如图5所示，控制器的输出为d轴电流参考值。但是，在实际应用中，基于这个框图的控制非常少见，通常会进行一定的简化。首先，在输入环节，直流电压及其参考值通常不会*方，也可以实现相同的控制目标。其次，直流电压控制并不需要很快的控制速度，因此前馈项 $p_{dc}$p_{dc} 可以省去，直接由PI控制器进行调节。另外，1.5 $u_d$u_d 的影响也可以合并进PI控制器的系数中，所以除法环节也可以省去。因此，更加实用的直流外环控制器如图6所示。

图6 实用的直流电压控制器

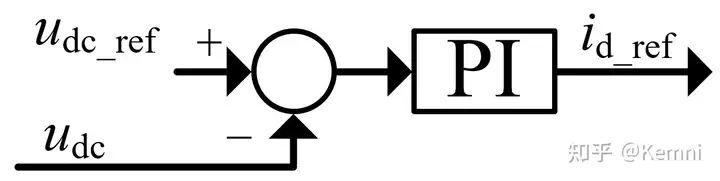
对于无功功率控制器，则可以直接采用开环计算出q轴电流参考值，或在开环计算的基础上增加反馈和前馈环节增强控制效果，控制框图如图7所示。

图7 无功功率外环控制

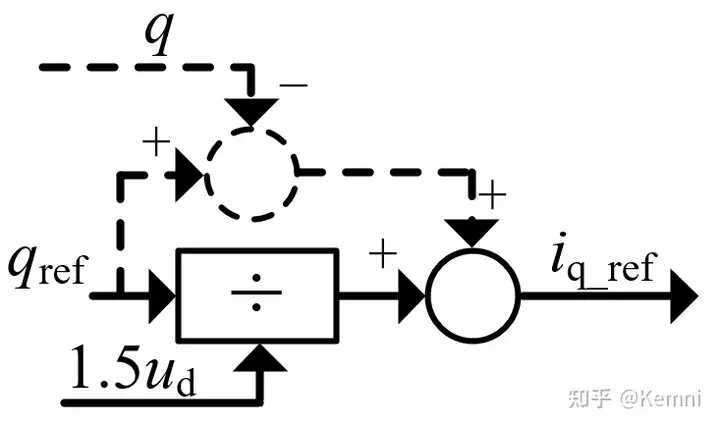
(2)PQ模式的功率环

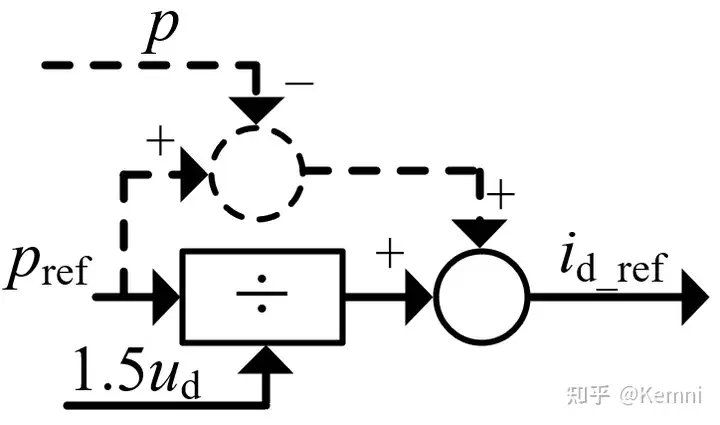
PQ模式的无功控制器与UdcQ模式的无功控制器相同。有功功率控制器与无功功率控制器的结构类似，输出d轴电流参考值，如图8所示。

图8 有功功率外环控制

3、锁相环

在控制框图中， $\omega t$\omega t 表示交流电压相位（通常为A相电压相位），通常是锁相环（Phase-Locked Loop, PLL）的输出，而锁相环本质上也是一个PI控制器，控制目标是使q轴电压为0，其原理如图9所示。

图9 锁相环（PLL）的原理

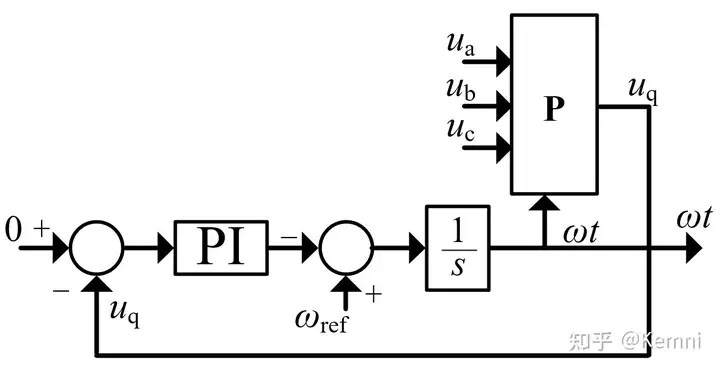
锁相环是典型的非线性环节。有研究指出，锁相环是可能引发震荡的原因之一。也有许多研究针对如何不用锁相环实现对于MMC的控制，但是本文不详细展开。

4、桥臂参考电压生成

在得到 $e_a、e_b、e_c$e_a、e_b、e_c 后，有名制的桥臂调制波（即桥臂电压参考值）则为：

$$\begin{gathered} e_{xp}=-e_x+\frac{U_{dcN}}{2} \\ {e}_{xn}=e_x+\frac{U_{dcN}}{2} \end{gathered}$$e_{xp}=-e_x+\frac{U_{dcN}}{2}\\ e_{xn}=e_x+\frac{U_{dcN}}{2}

------（13）

其中，x=a, b, c。虽然（13）已经得到有名制的桥臂调制波，但是通常需要将调制波归一化之后再送入阀控制器，归一化的过程是将有名制的桥臂调制波除以额定直流电压 $U_{dcN}$U_{dcN} ，即

$$\begin{gathered} e_{xp}^{\ast }=\frac{-e_x+\frac{U_{dcN}}{2}}{U_{dcN}}=-\frac{e_x}{U_{dcN}}+\frac{1}{2} \\ {e}_{xn}^{\ast }=\frac{e_x+\frac{U_{dcN}}{2}}{U_{dcN}}=\frac{e_x}{U_{dcN}}+\frac{1}{2} \end{gathered}$$e_{xp}^*=\frac{-e_x+\frac{U_{dcN}}{2}}{U_{dcN}}=-\frac{e_x}{U_{dcN}} + \frac{1}{2}\\ e_{xn}^*=\frac{e_x+\frac{U_{dcN}}{2}}{U_{dcN}}=\frac{e_x}{U_{dcN}} + \frac{1}{2}\\

------（13）

三、阀控制器

阀控制器最主要的作用在于两个方面：

1. 调制、电容电压均衡控制和脉冲生成：阀控制器接收换流器级控制器发来的桥臂调制波，经过调制环节得到桥臂投入的子模块数量，再经过电容电压均衡控制环节得到投入的具体子模块，最后经过半导体开关信号生成环节得到半导体开关器件的脉冲，从而实现对于桥臂输出电压的直接控制；
2. 实现高电位和地电位的电气隔离：换流器级控制及其之前的控制均发生在地电位，而MMC换流阀处于高电位，因此阀控制器还承担隔离地电位和高电位的作用。

其中，1中的脉冲生成已经在上一篇文章中详细说明，2中的阀控制器隔离高电位与地电位的作用主要是通过硬件隔离电路或芯片实现的。因此，本篇文章只展开说明调制和电容电压均衡环节。对于不同的子模块类型，虽然调制过程会有一定的差别，但是其基本原理是类似的，所以本文以结构最简单、状态最少的半桥子模块为例，阐述阀控制器的调制和电容电压均衡过程。

1、调制

（1）最*电*逼*调制

对于实际的柔性直流输电工程，桥臂中串联数量极为庞大的子模块（通常为上百至几百个），输出电*数目极多，直接采用非连续的阶梯波逼*连续的桥臂电压参考波是最为常见的调制方法，这类调制方法称为最*电*逼*调制（Nearest Level Modulation, NLM），如图10所示。最*电*逼*调制的优势是实现简便，适用于超多子模块数量的应用场景；其缺点主要是谐波特性相对较差，且谐波分布几乎没有规律。但是，对于超多电*数的应用场景来讲，谐波也是足够小的，在有些情况下甚至不需要进行谐波滤除。

图10 最*电*逼*调制桥臂输出电压示意图

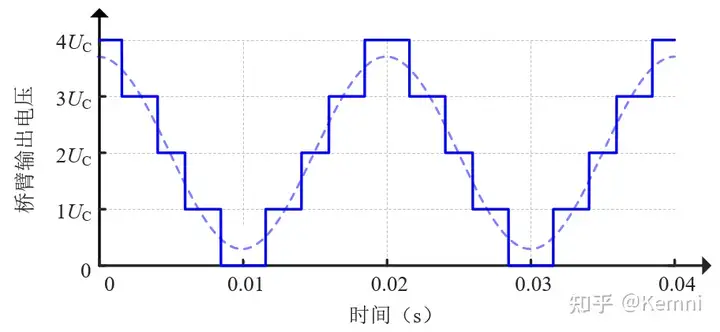
（2）PWM类调制（以载波移相调制为例）

除了高压直流输电场景之外，MMC还可以用于中压直流配电网、电机控制等领域。除此之外，在进行学术研究时，通常也需要搭建小容量的实验样机，从而对所提出的结构、控制、分析方法等进行验证。在这些情况下，MMC桥臂子模块数量通常较少（几个至几十个）。如果仍然采用最*电*逼*调制，那么输出电压、电流的谐波会比较大，控制效果也可能受到较大的影响。因此，在桥臂子模块数量较少的情况下，通常采用PWM类的调制方法，输出波形为PWM状的阶梯波。PWM类调制分为许多种，如PD、POD、APOD、特定谐波消去、载波移相调制等等。由于多电*PWM调制技术较为复杂，且笔者对于多电*调制技术的认识较为浅薄，因此此处只举载波移相调制（Phase Shift Modulation, PSM）作为一个例子以说明多电*PWM调制的方法。载波移相调制主要分为三角波生成和调制波和三角波比较两个步骤。

三角波生成：用N表示桥臂中子模块的数量。在阀控制器中生成N个在0~1之间变化的三角波，且每个相邻三角波之间相位错开 $\frac{\pi }{N}$\frac{\pi}{N} ，得到一组三角波如下（下图中以三角波频率500Hz、N=4为例）：

图11 载波移相调制三角波示意图

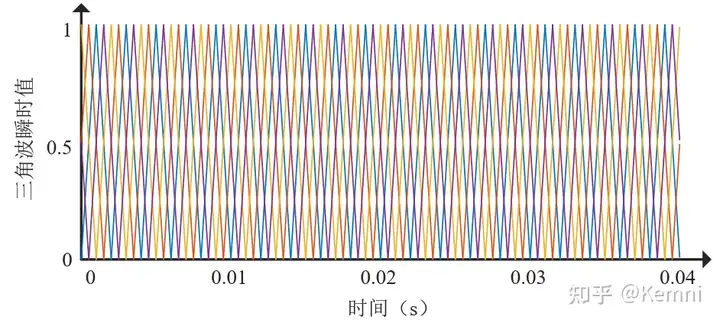
调制波与三角波比较：将调制波与每个载波比较。用Sa表示桥臂投入的子模块数量，Sa的值就等于调制波高于载波的数量。例如，在某时刻，调制波比三个载波高、比一个载波低，则该时刻Sa=3。

图12 载波移相调制的Sa函数波形示意图

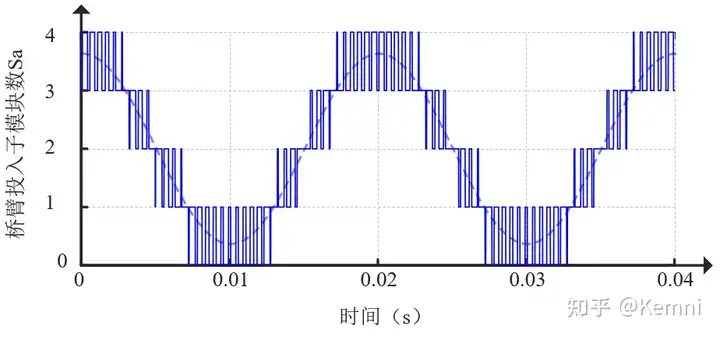
2、电容电压均衡控制与脉冲生成

调制环节计算出了每个时刻应当投入和旁路的子模块数量，但是并没有得到究竟是哪些子模块投入、哪些子模块旁路。如图13、14所示，MMC在运行的过程中，如果子模块投入，那么桥臂电流会流入（桥臂电流方向为正，图13）或流出（桥臂电流方向为负，图14）子模块电容，导致电容电压的变化；而被旁路的子模块电容电压则不会变化（不考虑损耗）。“部分投入、部分旁路”这样的桥臂子模块运行特点就造成了同一个桥臂内各子模块的电容电压可能不均衡。均衡电容电压是阀控制器的重要功能之一。

图13 电流正向时，投入和旁路的子模块电流流通情况

图14 电流为负向时，投入和旁路的子模块电流流通情况

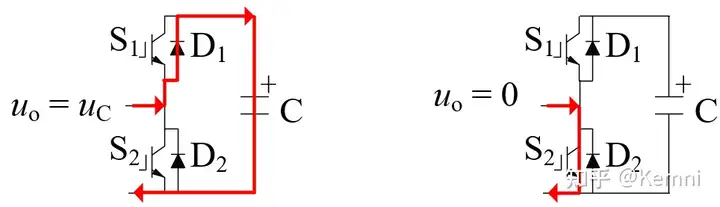
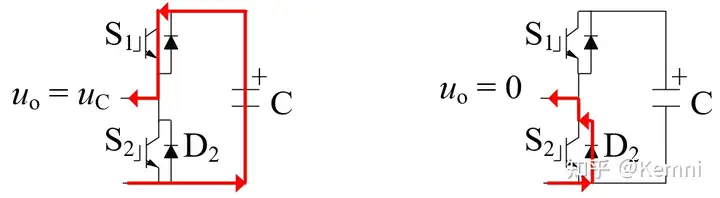
半桥子模块只有投入和旁路两个状态。仍用Sa表示一个桥臂中投入的子模块数量。假设在某时刻，桥臂内各子模块电容电压并不相等。为了使电容电压相等，如果电流为正（投入的子模块电容流入电流，电压上升），那么阀控制器选择电容电压最低的Sa个子模块投入、另外(N-Sa)个子模块旁路。这些投入的子模块电容电压就会上升。如果桥臂电流为负，那么阀控制器选择电容电压最高的Sa个子模块投入、(N-Sa)个子模块旁路。那么这些被投入的子模块电容电压就会下降。这种选择机制可以使得同一个桥臂内子模块电容电压无论任何时刻都能保证*似相等，这就是电容电压均衡控制的基本原理。

然而，需要说明的是，电容电压*衡控制的目标并非使子模块电容电压完全相等，而是将桥臂内子模块电容电压的偏差控制在一定范围内即可。由于MMC运行过程中电容电压是不断变化的，所以实际上电容电压的排序结果也是不断变化的。然而，如果每时每刻（即每个时钟周期）控制程序都对电容电压排序、并根据排序结果不断改变子模块状态，那么不仅浪费硬件计算资源，而且还会使得电力电子开关不断开关，增大MMC的损耗，非常不经济，而且也没有必要这样做。下面举例说明：

假设t1时刻四个电容电压分别为1000V、1025V、1030V、1010V，电流方向为正。如果Sa=3，那么阀控程序将投入1、2、4号子模块电容，旁路3号子模块的电容。此时，1、2、4三个电容被桥臂电流充电，电容电压上升。假设t1的下一个时刻t2时（t1与t2间隔很短），四个电容电压分别变成了1020V、1045V、1030V、1030V。假设Sa仍等于3，如果t2时刻立即对新的电容电压重新排序并动作，那么应当投入1、3、4号子模块。在t1至t2这一短暂时间内，桥臂投入子模块数并没有发生变化，而2号子模块从投入变为旁路、3号子模块从旁路变为投入，总共四个半导体器件发生动作。然而，t2时四个电容电压偏差并不大，如果继续采用t1时刻的排序结果，就可以避免这四个半导体器件的动作，从而减小开关损耗。因此，在实际应用时，为了减少半导体开关的动作次数以降低MMC的损耗，并不会在控制器的每个时钟周期都对子模块排序一次，只在电容电压偏差较大时再重新排序。

虽然降低电容电压排序频率会使电容电压的均衡程度降低，但是只要合理选择排序频率或排序的触发条件，那么电容电压偏离就仍是可以接受的。

基于投入子模块数量、子模块电容电压排序结果和桥臂电流方向，阀控制器生成控制开关信号，控制换流阀中的子模块完成投入和旁路，从而实现对于桥臂输出电压的直接控制。

四、附录：关于MMC直流侧等效电容的说明

在本文第二节第2小节提到了MMC直流侧等效电路，其中包含一个等效电容，容值为：

$C_{eq}=\frac{6C_{sm}}{N}$C_{eq}=\frac{6C_{sm}}{N} ，其中 $C_{sm}$C_{sm} 为子模块电容值，N为桥臂子模块数量。有些学者认为由于子模块内含有电容，所以MMC的直流侧等效电容天然存在，这是不正确的。MMC直流侧等效电容的存在主要是采用特定的调制方法造成的结果。

如上文所述，MMC计算桥臂调制波时的计算结果为：

$$\begin{gathered} e_{xp}^{\ast }=-\frac{e_x}{U_{dcN}}+\frac{1}{2} \\ {e}_{xn}^{\ast }=\frac{e_x}{U_{dcN}}+\frac{1}{2} \end{gathered}$$e_{xp}^*=-\frac{e_x}{U_{dcN}} + \frac{1}{2}\\ e_{xn}^*=\frac{e_x}{U_{dcN}} + \frac{1}{2}\\桥臂调制波是一个在0~1之间变化的变量，其值本质上表示任意时刻桥臂内有多少比例的子模块投入。值得注意的是，上、下桥臂调制波的特点是，二者之和为常数1。这就表明，上桥臂与下桥臂投入的子模块数量之和必须刚好与一个桥臂的子模块数量N相等。而上、下桥臂的输出电压之和又刚好就是直流电压。这就意味着，直流电压必须与电容电压成比例关系，且比例系数为N，也就是：

$u_{dc}=N{u}_C$u_{dc}=Nu_C

其中， $u_C$u_C 表示电容电压（在电容电压均衡控制的作用下，认为所有电容电压*似相等）。由于电容电压必须是连续的，不能阶跃变化，因此直流电压和电容电压的比例关系就直接决定了直流电压在也不可能迅速变化，也就是在直流电压变化的过程中，等效于出现了一个并联在MMC直流侧的电容。

对于每一相来讲，任意时刻上、下桥臂投入电容数量之和为N。表面看每一相的等效电容是Csm/N。在电容电压*衡控制的作用下，桥臂内各个子模块电容轮流投入，电容电压共同上升，时间常数被拉大。因此，每一相的等效电容值为2Csm/N，而三相等效电容为6Csm/N。

上述调制方式的特点是，在计算桥臂调制波时，归一化的过程是将有名制的桥臂参考电压除以直流电压得到的。这种方式称为直接调制。直接调制的优势是实现简单、桥臂电容电压自*衡（即：如果有扰动使某个桥臂的电容电压整体与其他桥臂不同，在一段时间后可以自然恢复），但是缺点是会将子模块电容耦合到MMC的直流侧使直流电压控制速度变慢，而且等效电容还可能与直流侧等效电感相互作用导致震荡的发生。除此之外，直接调制是MMC产生环流的重要原因之一。

与直接调制相对的是间接调制，其特点是是在计算桥臂调制波时并不除以直流额定电压，而是除以桥臂电容电压之和的采样值。间接调制方式下，直流电压与电容电压并不一定是比例关系，因此不会出现直流等效电容的问题，但是间接调制方式下无法实现桥臂电容电压自*衡，需要配合额外的控制。

下一篇文章将介绍子模块电容电压波动和环流的产生，敬请期待。