动手学深度学习v2-09-01-Softmax回归

一、softmax回归

• softmax回归实际上是用于解决分类问题的。
  

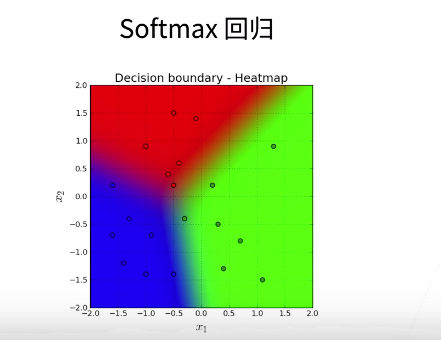
1. 回归和分类的区别

2.如何从回归转换到分类

3.分类问题

• 一般的分类问题并不与类别之间的自然顺序有关。
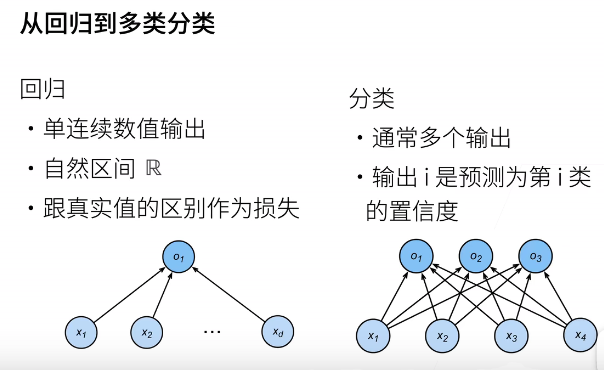
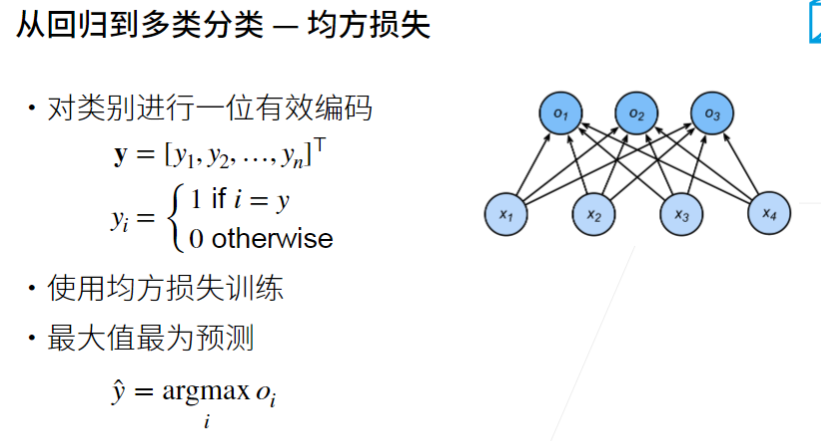
• 发明了一种表示分类数据的简单方法：独热编码（one-hot encoding）。独热编码是一个向量，它的分量和类别一样多。类别对应的分量设置为1，其他所有分量设置为0。 在我们的例子中，标签 y 将是一个三维向量，其中 (1,0,0) 对应于“猫”、 (0,1,0) 对应于“鸡”、 (0,0,1) 对应于“狗”：
  

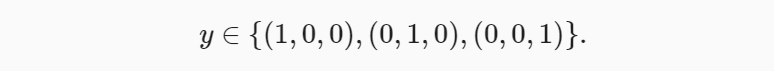
4.网络结构

• softmax回归也是一个单层神经网络。由于计算每个输出 o1、o2和o3取决于所有输入x1、x2、x3和x4 ，所以softmax回归的输出层也是全连接层。
  

5.全连接层的参数开销

• 在深度学习中，全连接层无处不在。 然而，顾名思义，全连接层是“完全”连接的，可能有很多可学习的参数。
• 对于任何具有d个输入和q个输出的全连接层，参数开销为O(dq)
• 将 d 个输入转换为 q 个输出的成本可以减少到 O(\(\frac{dq}{n}\)) ，其中超参数 n 可以由我们灵活指定，以在实际应用中平衡参数节约和模型有效性

6.softmax运算

• 采取的主要方法是将模型的输出视作为概率。我们将优化参数以最大化观测数据的概率。为了得到预测结果，我们将设置一个阈值，如选择具有最大概率的标签。
  

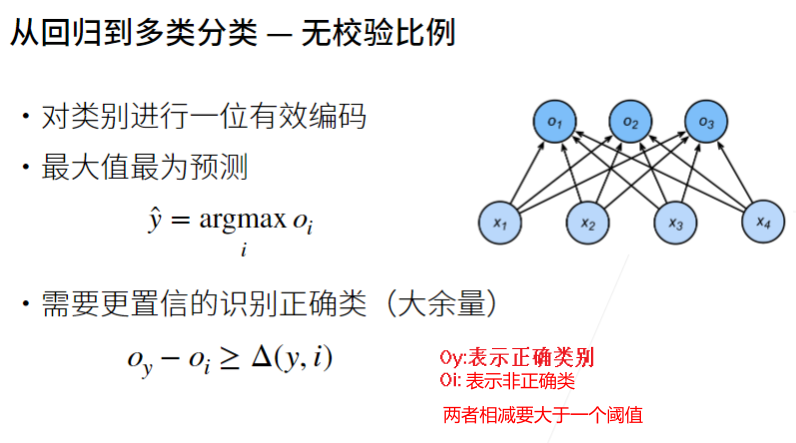
• 为了将未归一化的预测变换为非负并且总和为1，同时要求模型保持可导。我们首先对每个未归一化的预测求幂，这样可以确保输出非负。为了确保最终输出的总和为1，我们再对每个求幂后的结果除以它们的总和。
  

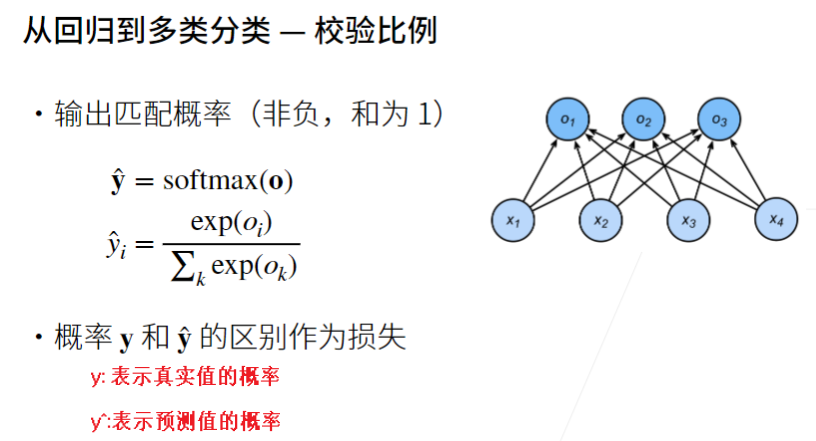
结论：尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。因此，softmax回归是一个线性模型。

7 损失函数

• 我们需要一个损失函数来度量预测概率的效果。

7.1 对数似然

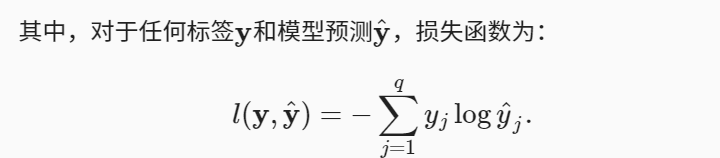
7.2 交叉熵损失

• 所有标签分布的预期损失值。
• 分类问题最常用的损失之一
• 从两方面来考虑交叉熵分类目标：（i）最大化观测数据的似然；（ii）最小化传达标签所需的惊异。
  

8 模型预测和评估

• 在训练softmax回归模型后，给出任何样本特征，我们可以预测每个输出类别的概率。
• 通常我们使用预测概率最高的类别作为输出类别。
• 如果预测与实际类别（标签）一致，则预测是正确的。

9 小结