QOJ1087

题目链接

---

题解

考虑按位思考。将其转换成 \(x_i=0,1\) 的特殊性质，假设此时的二进制位为第 \(k\) 为，那操作就相当于如果 \(x_i\&2^k=1\) 那就等价于特殊性质 \(x_i=1\)，反之为 \(0\)。可以差分在 \(O(n^2)\) 的时间复杂度内求出那些位置被覆盖了，即涂了 \(1\)，得出 \(a\) 数组（这时定义不合法限制为 \(x_i=0\) 并且 \(\exists xiabiao,l_i \le xiabiao \le r_i\) 且 \(a_{xiabiao}=1\)，这个可以 \(O(m)\) 结合 \(a\) 数组的前缀和求出），同时也可以顺便求出那些位置只被涂了一次的点 \(1\)，得出 \(b\) 数和右端点向前走的组。然后考虑删除一个限制的印象：

• 删掉 \(x_i=0\) 的限制，那么对于 \(a\) 数组不会有改变，如果不合法限制就只有他一个，那么就是对的，反之就是错的。\(O(1)\) 可以求出。
• 删掉 \(x_i=1\) 的限制，就会使 \(a\) 数组中的一些 \(1\) 变为 \(0\)。这个时候 \(b\) 数组就派上了用场，我们先通过 \(b\) 数组求出对于每一个不合法限制的左端点向后走的第一个只被涂了一次的点和右端点向前走的第一个只被涂了一次的点的位置，再将所有不合法限制的左端点的值取 \(max\)，记为 \(r\)，所有不合法限制的右端点的值取 \(min\)，记为 \(l\)（这个可以 \(O(n+m)\) 解决，而且 \(l\) 和 \(r\) 是不变的），这个时候就要分类讨论。
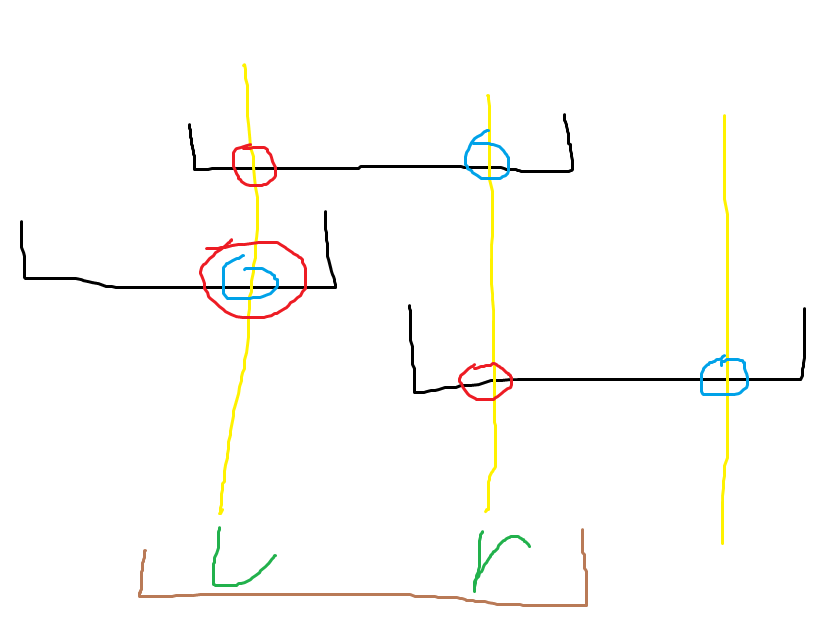
  如果是这样，黄线为只被涂了一次的点的位置，黑区间为不合法区间，蓝圈为 \(min\)，红圈为 \(max\)，棕区间为这个1限制， \(l\le r\) 时，只要这个1限制包含了 \(l\) 和 \(r\)，那就可以，否则就不可以。
  
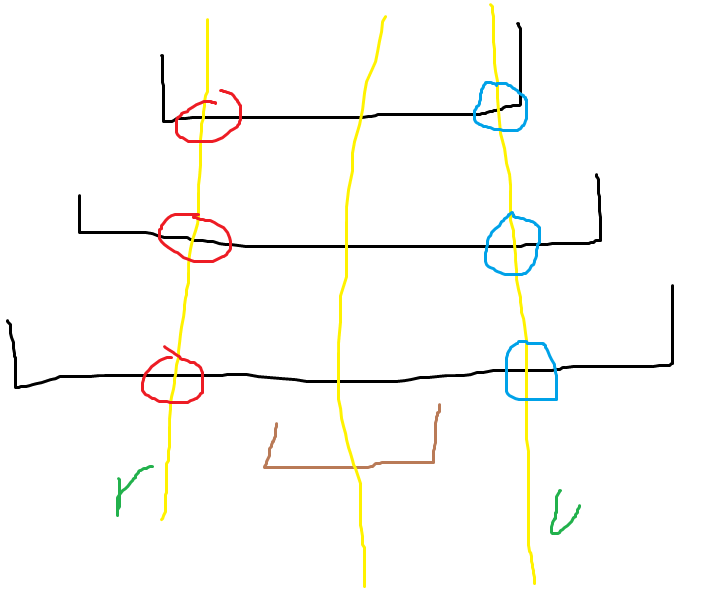
  如果是这样，\(r< l\) 时，1限制不包含了 \(l\) 和 \(r\)，但这个图明显可以，因为中间有一个只被涂了一次的点，那删除这个点明显可以使不合法限制变得合法，所以只需要判断这个1限制之间有没有只被涂了一次的点。

这两个判断可以 \(O(m)\) 得出

所以除去常数后，整个的复杂度就为 \(O((n+m)log V)\)