【LeetCode】236. 二叉树的最近公共祖先

leetcode

 

解题思路

寻找二叉树中两个节点的最近公共祖先（LCA）的核心思路是利用​​后序遍历​​的特性（左→右→根）实现​​自底向上​​的查找。关键点在于：

1. ​​递归终止条件​​：当前节点为空或是目标节点之一时直接返回
2. ​​子树搜索​​：递归搜索左右子树
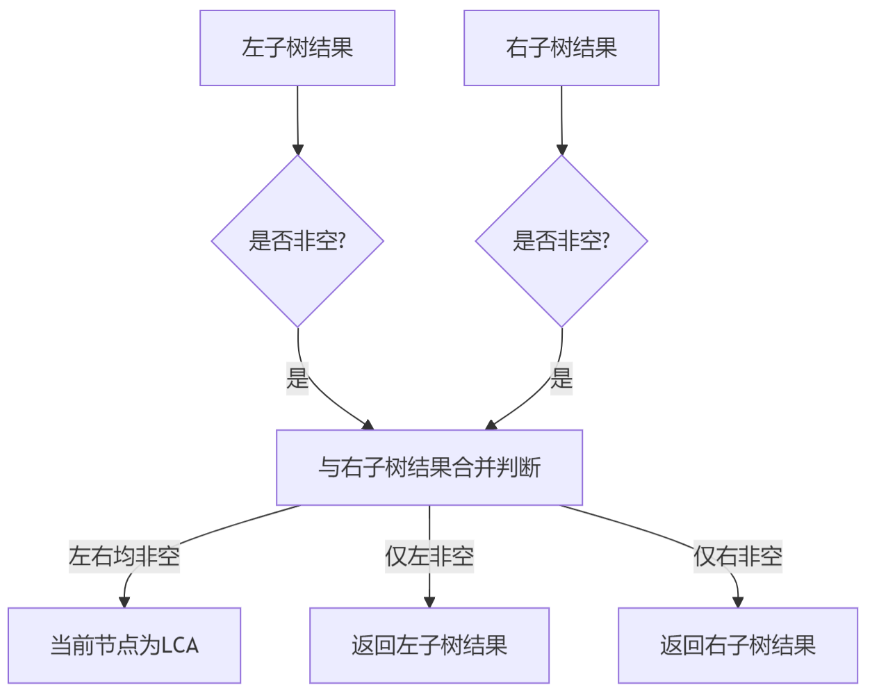
3. ​​结果合并​​：
   • 若左右子树均找到目标节点 → 当前节点为LCA
   • 若仅一侧找到目标节点 → 返回该侧结果
   • 均未找到 → 返回nil

本质是​​DFS回溯​​过程，利用递归栈记录路径信息

关键步骤

1. ​​终止条件处理​​：节点为nil/p/q时直接返回
2. ​​左右子树递归​​：分别搜索左/右子树
3. ​​LCA判断逻辑​​：

   

代码实现

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    // 终止条件: 遇到nil/p/q直接返回
    if root == nil || root == p || root == q {
        return root
    }

    // 递归搜索左右子树
    left := lowestCommonAncestor(root.Left, p, q)
    right := lowestCommonAncestor(root.Right, p, q)

    // 结果合并判断
    switch {
    case left != nil && right != nil: // 左右均找到 --> 当前为LCA
        return root
    case left != nil:
        return left // 仅左子树找到
    default:
        return right // 仅右子树找到或均未找到
    }
}

示例测试

func main() {
    // 示例1：LCA(5,1)=3
    node3 := &TreeNode{Val: 3}
    node5 := &TreeNode{Val: 5}
    node1 := &TreeNode{Val: 1}
    node3.Left, node3.Right = node5, node1
    fmt.Println(lowestCommonAncestor(node3, node5, node1).Val) // 3

    // 示例2：LCA(5,4)=5
    node4 := &TreeNode{Val: 4}
    node2 := &TreeNode{Val: 2, Right: node4}
    node5.Left = &TreeNode{Val: 6}
    node5.Right = node2
    fmt.Println(lowestCommonAncestor(node3, node5, node4).Val) // 5

    // 示例3：LCA(1,2)=1
    node1.Left = &TreeNode{Val: 2}
    fmt.Println(lowestCommonAncestor(node1, node1, node1.Left).Val) // 1
}

复杂度分析

指标	值	说明
​​时间复杂度​​	O(n)	每个节点访问1次（n为节点数）
​​空间复杂度​​	O(h)	递归栈深度（h为树高）
最坏情况	O(n)	树退化为链表时（h=n）

关键点总结

1. ​​后序遍历特性​​：自底向上回溯是核心
2. ​​四种返回值情况​​：
   • 当前节点为LCA → 左右子树均找到目标
   • 目标在左子树 → 返回左子树结果
   • 目标在右子树 → 返回右子树结果
   • 均未找到 → 返回nil
3. ​​边界处理​​：
   • 节点为自身祖先（p的LCA是p）
   • 空树直接返回nil
4. ​​适用性​​：适用于普通二叉树（无需BST特性）